Download as PDF, PPTX
Uploaded byRohit Khurana
Surge pricing mc_presentation
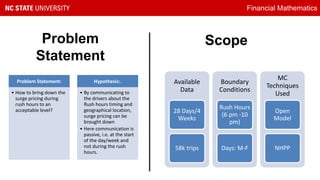
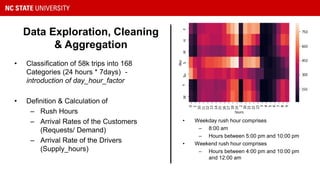
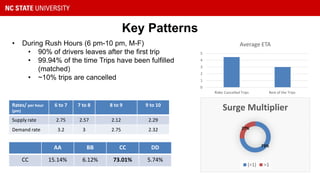
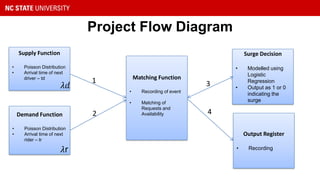
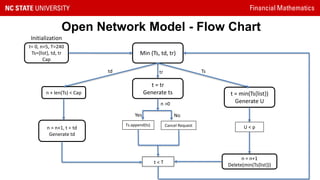
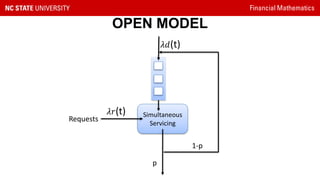
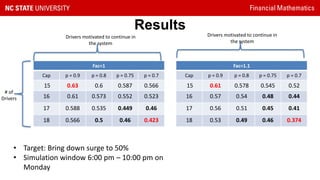
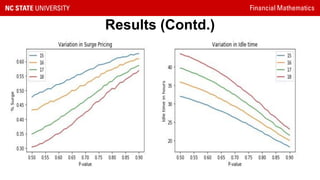
This document presents a study on reducing surge pricing for cab hailing services during rush hours. It analyzes data from 58,000 taxi trips over 28 days to identify rush hour periods between 6-10pm Monday through Friday with high demand. An open network Poisson model is used to simulate driver and rider arrival rates. The model shows communicating rush hour timing and locations to drivers can decrease surge pricing by up to 10% by motivating more drivers to continue working during these periods. However, the assumptions require validation and driver psychology was not fully considered. Future work could focus on demand-supply equilibrium and behavioral factors.
Surge pricing mc_presentation
- 1. REDUCING SURGE PRICESFOR CAB HAILING SERVICE Presented by Muktanidhi Dhotrad, Rohit Khurana, Sandeep Girada Under the Guidance of Dr. Yunan Liu Yining Huang Apr 2019 Financial Mathematics
- 2. Problem Statement Financial Mathematics Problem Statement: •How to bring down the surge pricing during rush hours to an acceptable level? Hypothesis:. • By communicating to the drivers about the Rush hours timing and geographical location, surge pricing can be brought down • Here communication is passive, i.e. at the start of the day/week and not during the rush hours. Available Data 28 Days/4 Weeks 58k trips Boundary Conditions Rush Hours (6 pm -10 pm) Days: M-F MC Techniques Used Open Model NHPP Scope
- 3. Data Exploration, Cleaning &Aggregation • Classification of 58k trips into 168 Categories (24 hours * 7days) - introduction of day_hour_factor • Definition & Calculation of – Rush Hours – Arrival Rates of the Customers (Requests/ Demand) – Arrival Rate of the Drivers (Supply_hours) • Weekday rush hour comprises – 8:00 am – Hours between 5:00 pm and 10:00 pm • Weekend rush hour comprises – Hours between 4:00 pm and 10:00 pm and 12:00 am
- 4. Key Patterns 0 1 2 3 4 5 Rider CancelledTrips Rest of the Trips Average ETA 73% 27% Surge Multiplier (=1) >1 AA BB CC DD CC 15.14% 6.12% 73.01% 5.74% 𝜆𝑑 𝜆𝑟 • During Rush Hours (6 pm-10 pm, M-F) • 90% of drivers leaves after the first trip • 99.94% of the time Trips have been fulfilled (matched) • ~10% trips are cancelled Rates/ per hour (pm) 6 to 7 7 to 8 8 to 9 9 to 10 Supply rate 2.75 2.57 2.12 2.29 Demand rate 3.2 3 2.75 2.32
- 5. Definitions Financial Mathematics • Supply_hours: Total hours all partners (drivers) were online, en route, or on trip in the given hour • Demand/ Requests: Total requests in the given hour • Surge Pricing: When Supply > Demand, leads to surge pricing • List of Service Times – Ts • Total number of Drivers active in the System – N • Model • Open Network (p=0.9) • Probability of 90 % drivers leaving the system after completion of 1 trip in a day • With (1-p=0.1) probability of 10% returning back to system
- 6. Project Flow Diagram SupplyFunction • Poisson Distribution • Arrival time of next driver – td Demand Function • Poisson Distribution • Arrival time of next rider – tr 𝜆𝑑 𝜆r Matching Function • Recording of event • Matching of Requests and Availability Surge Decision • Modelled using Logistic Regression • Output as 1 or 0 indicating the surge Output Register • Recording 1 2 3 4
- 7. Financial Mathematics Open NetworkModel - Flow Chart t= 0, n=5, T=240 Ts={list}, td, tr Cap Initialization Min (Ts, td, tr) t = tr Generate ts Ts.append(ts) Cancel Request t < T n + len(Ts) < Cap n = n+1, t = td Generate td t = min(Ts{list}) Generate U U < p n = n+1 Delete(min(Ts{list})) Tstrtd n >0 Yes No
- 8.
- 9. Financial Mathematics Results Fac=1 Cap p= 0.9 p = 0.8 p = 0.75 p = 0.7 15 0.63 0.6 0.587 0.566 16 0.61 0.573 0.552 0.523 17 0.588 0.535 0.449 0.46 18 0.566 0.5 0.46 0.423 • Target: Bring down surge to 50% • Simulation window 6:00 pm – 10:00 pm on Monday # of Drivers Drivers motivated to continue in the system Fac=1.1 Cap p = 0.9 p = 0.8 p = 0.75 p = 0.7 15 0.61 0.578 0.545 0.52 16 0.57 0.54 0.48 0.44 17 0.56 0.51 0.45 0.41 18 0.53 0.49 0.46 0.374 Drivers motivated to continue in the system
- 10.
- 11. Recommendations • Passively communicatingdrivers about the rush hours and location brings down the count of surge pricing.
- 12. • Model useslot of assumption, that needs to be validated. • Psychological behavior of the partner/ drive does play a role and that requires attention. • Possibility of breach of Demand & Supply Equilibrium to be studied. Future Enhancements
- 13.