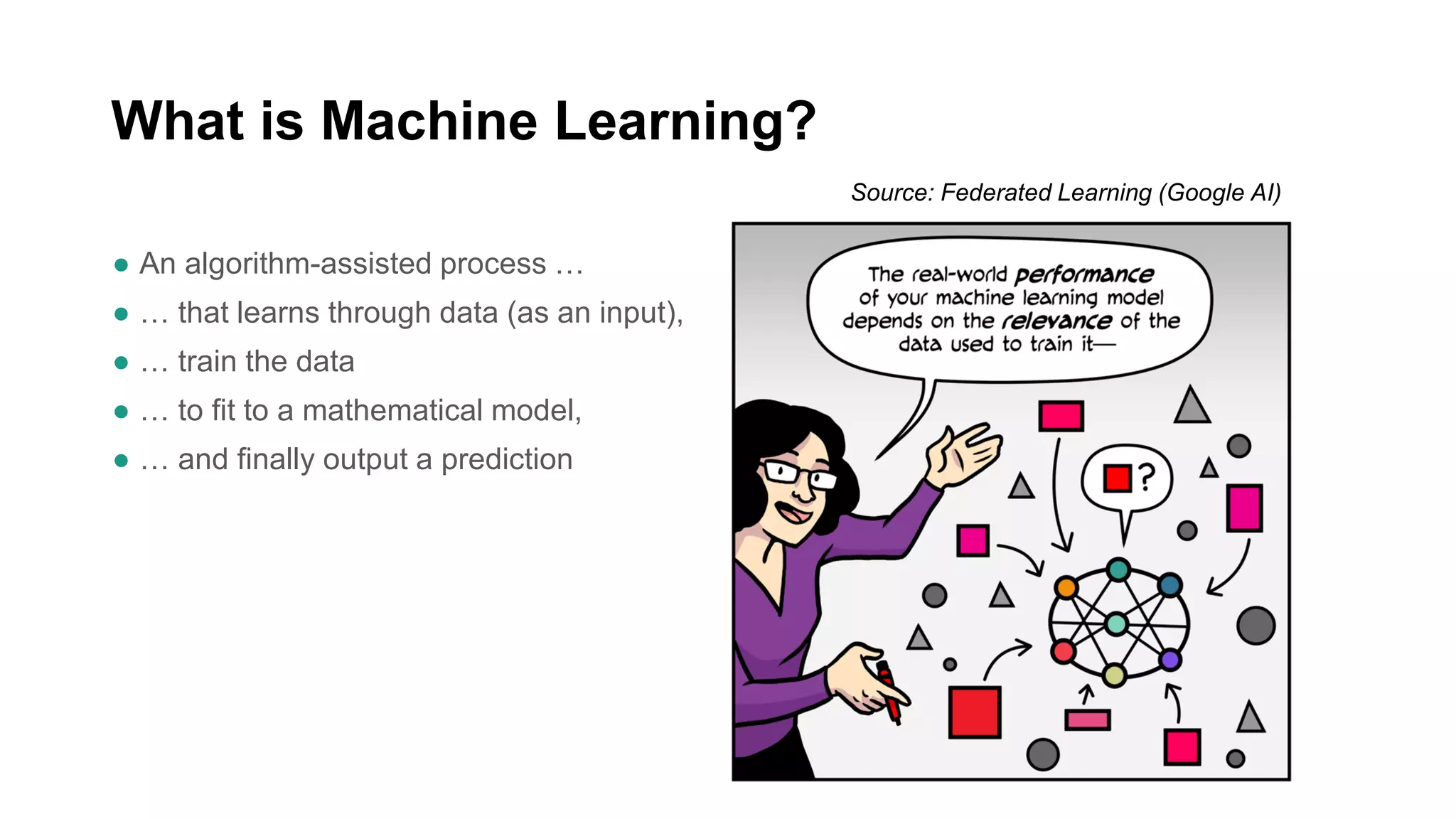
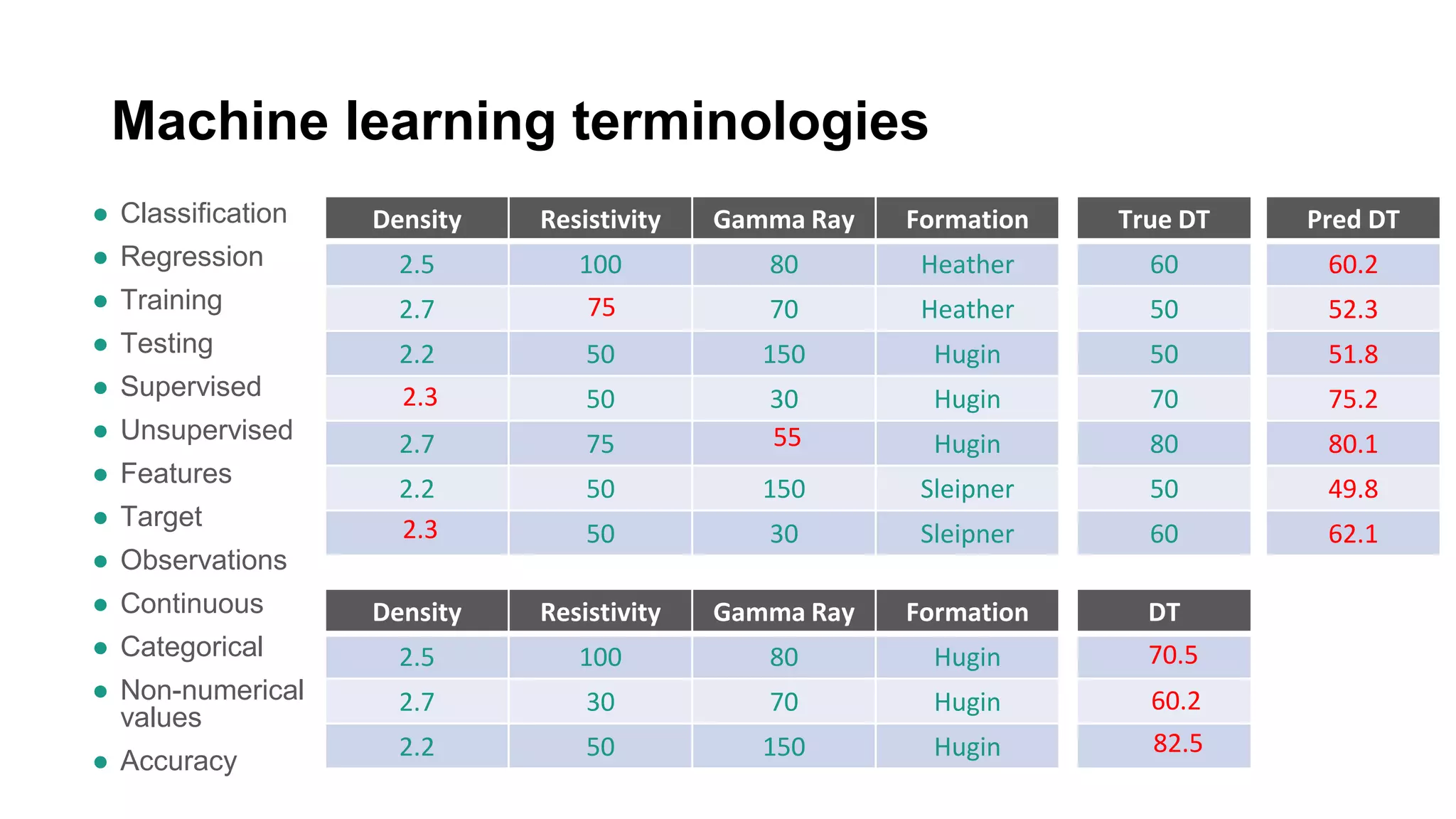
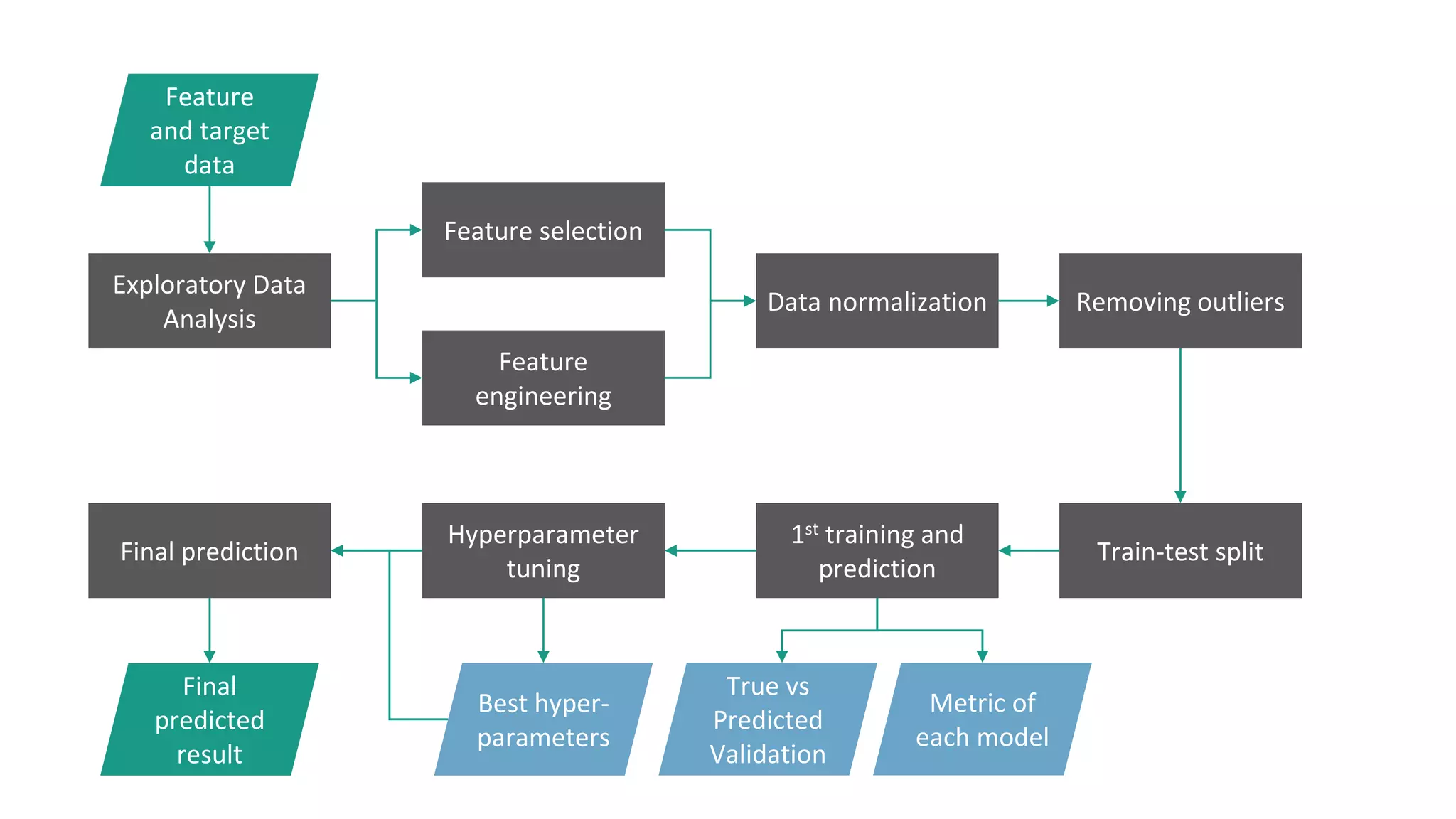
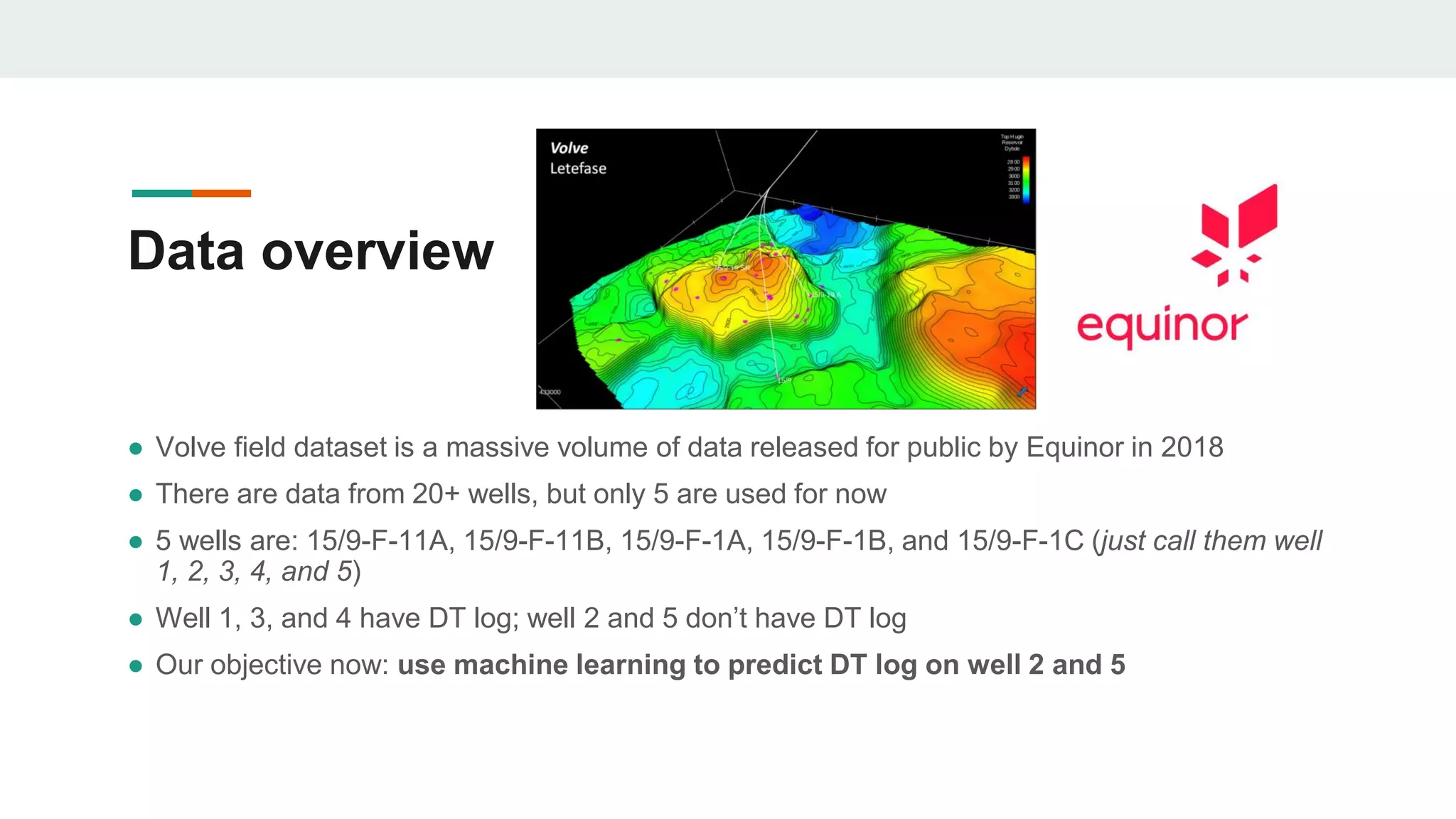
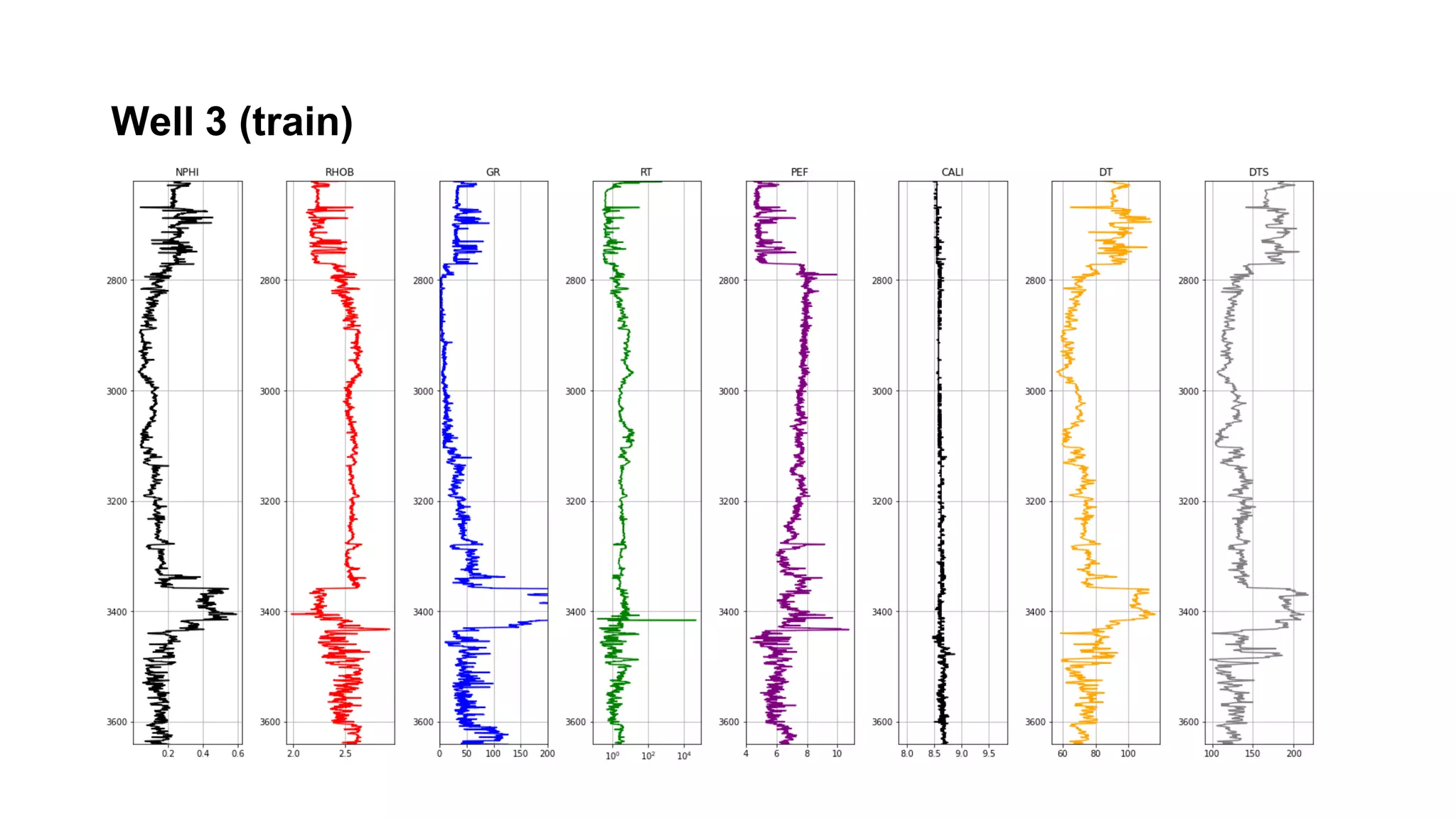
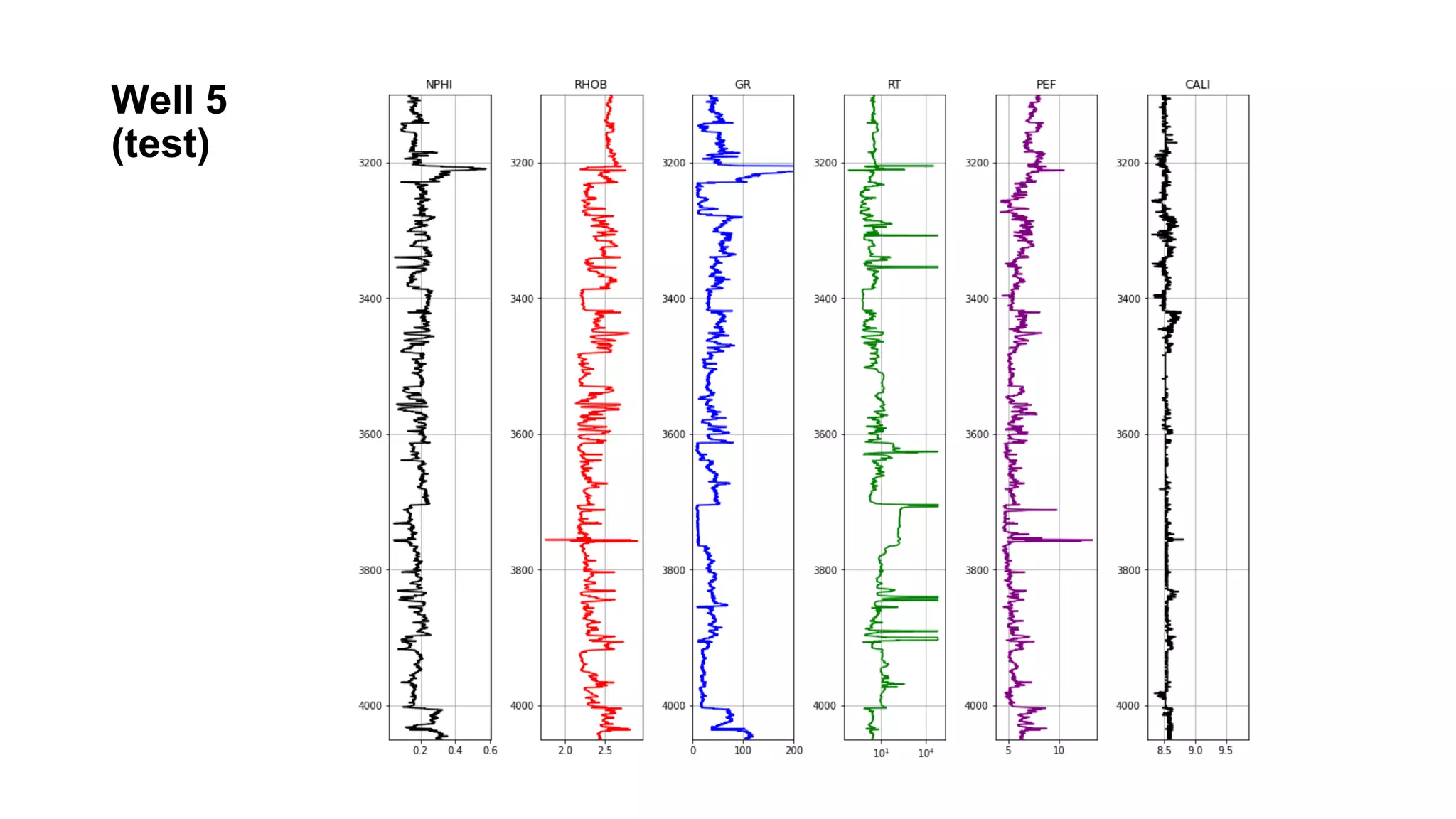
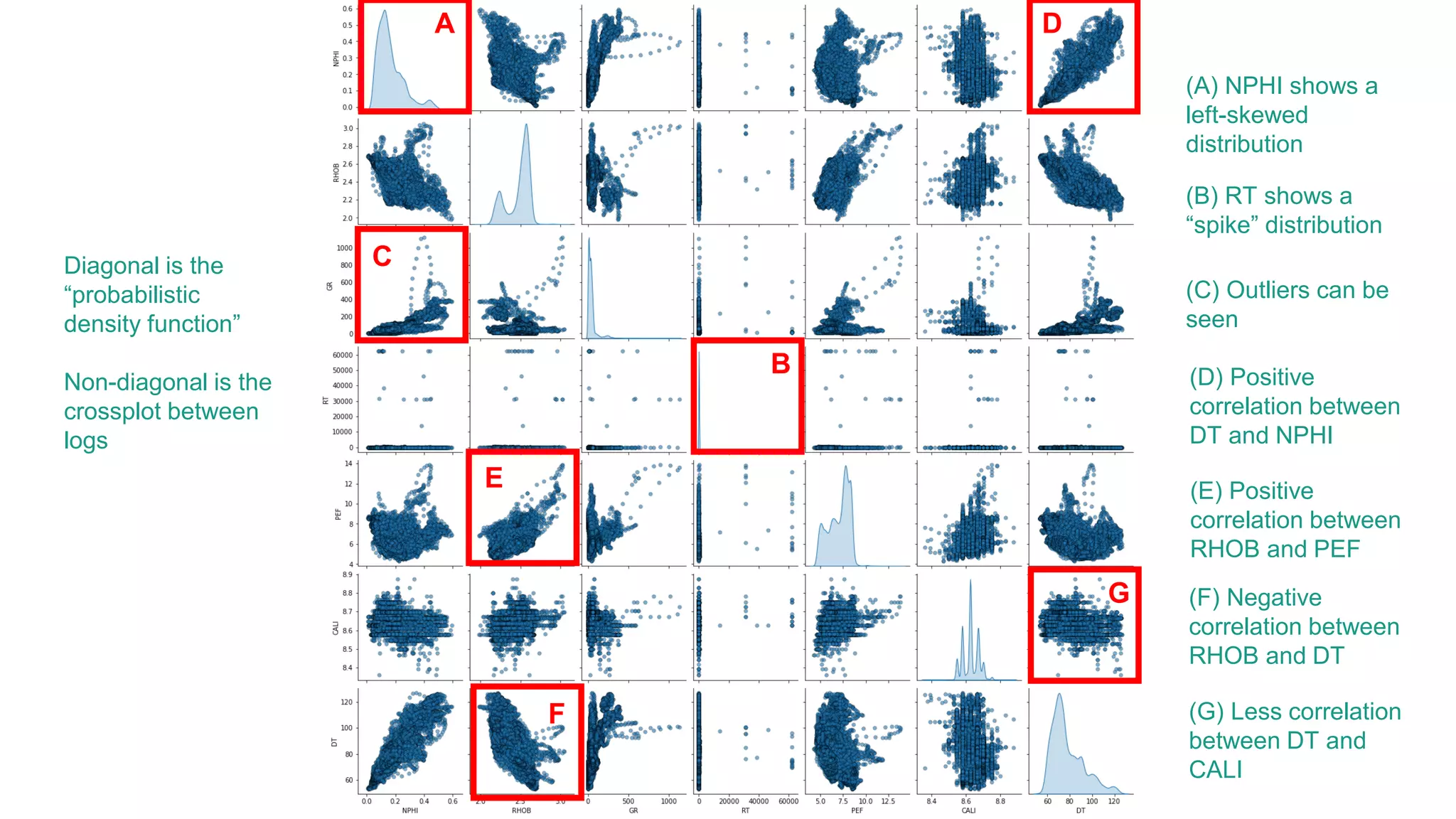
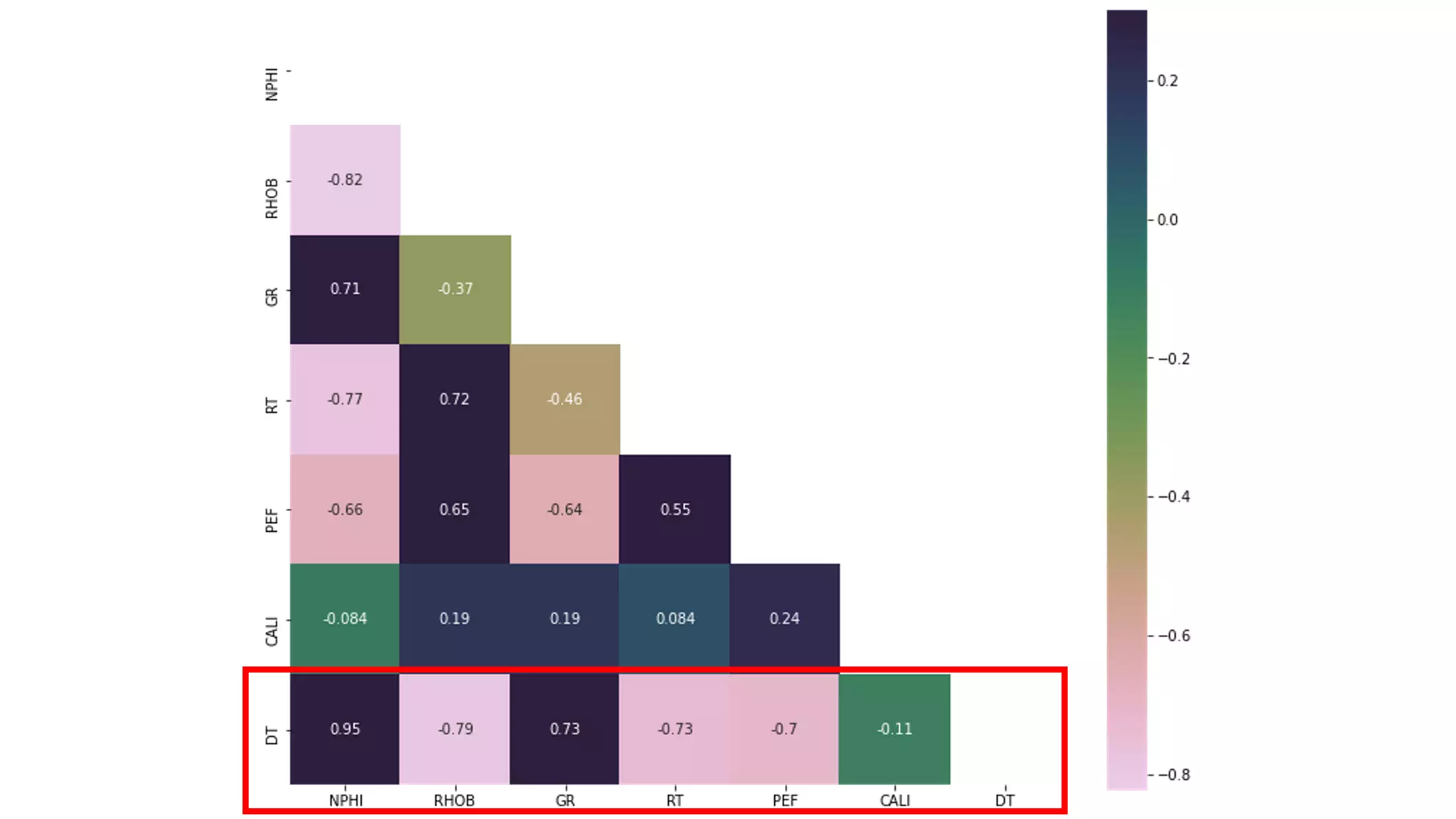
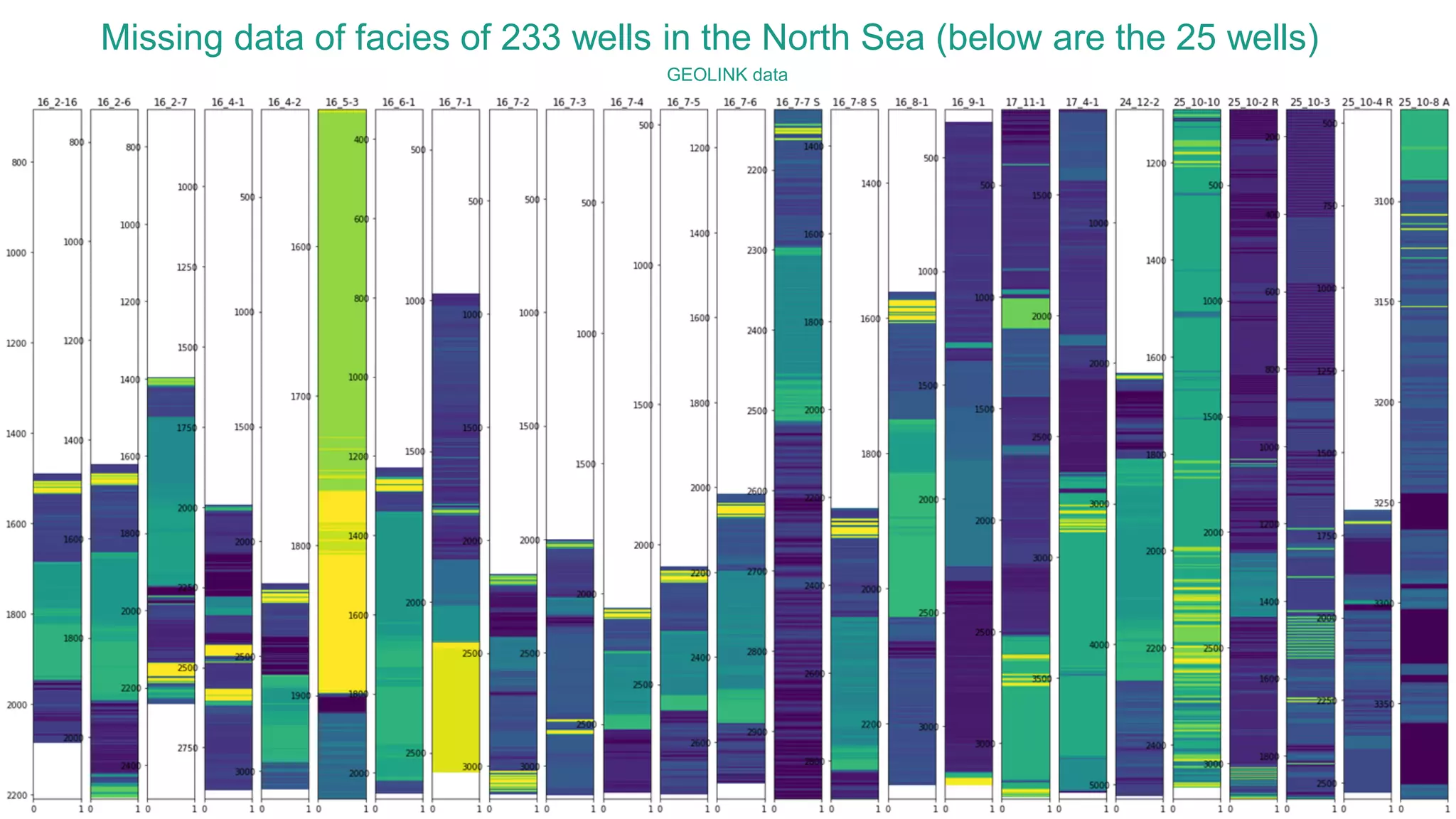
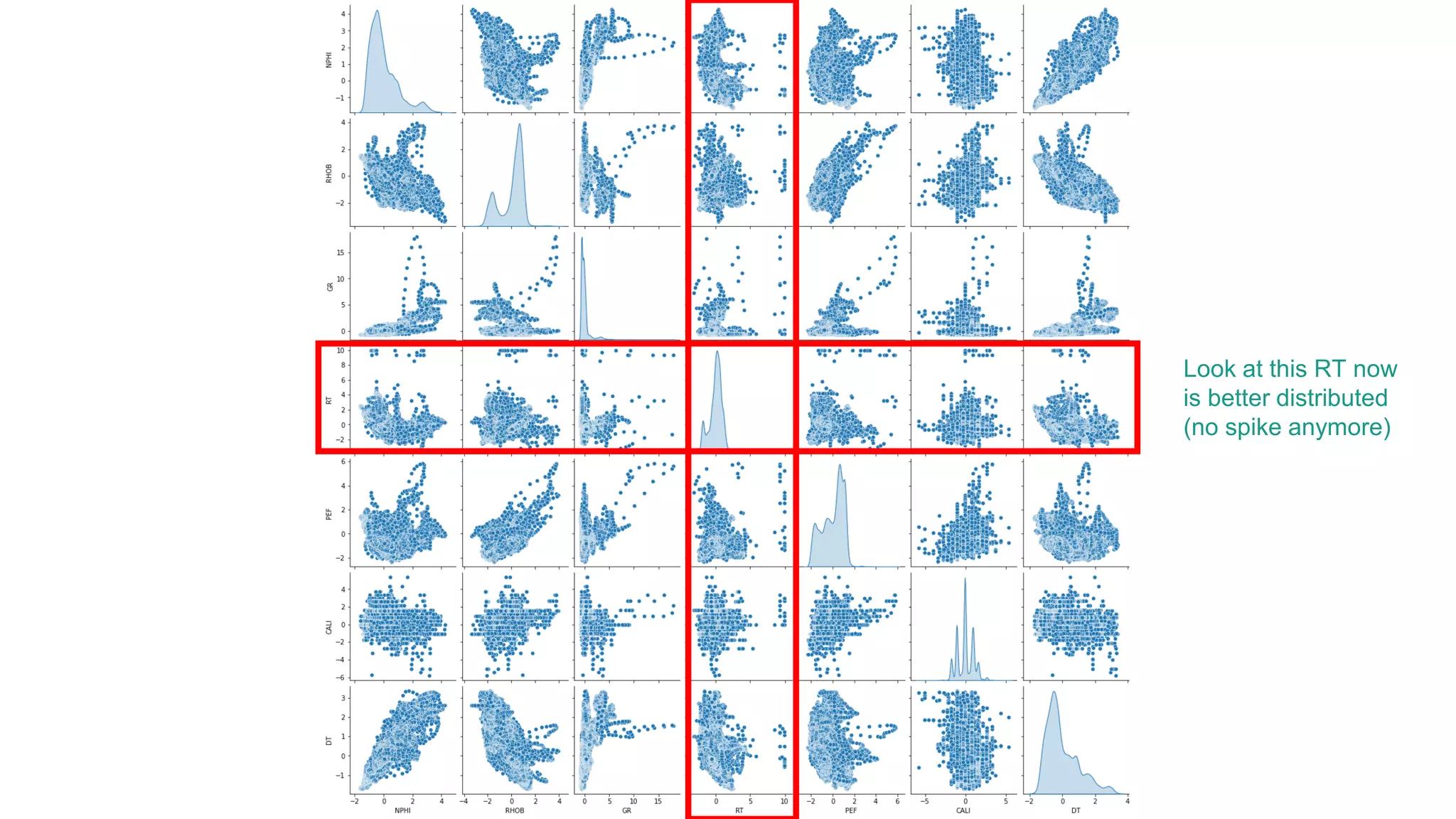
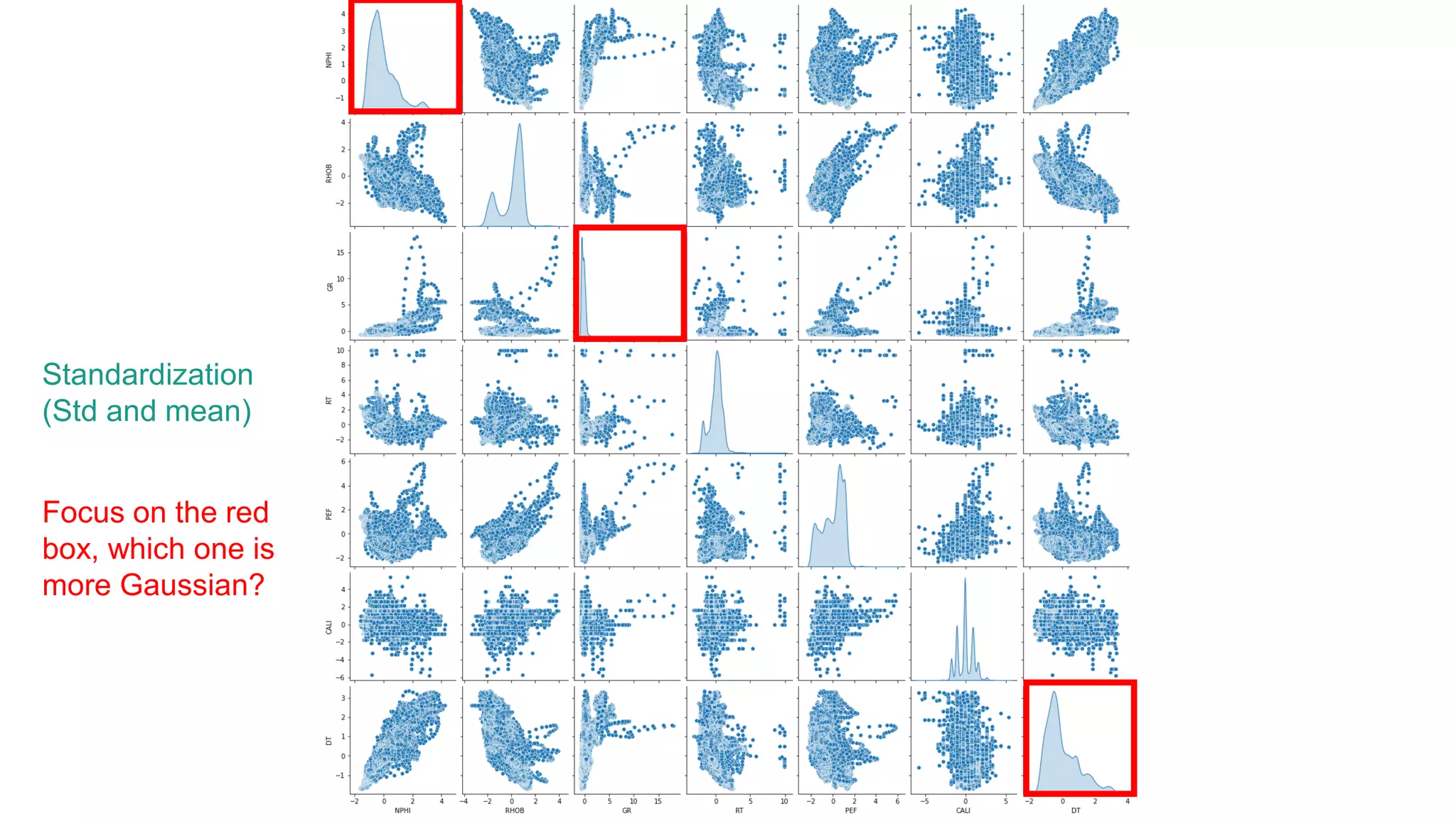
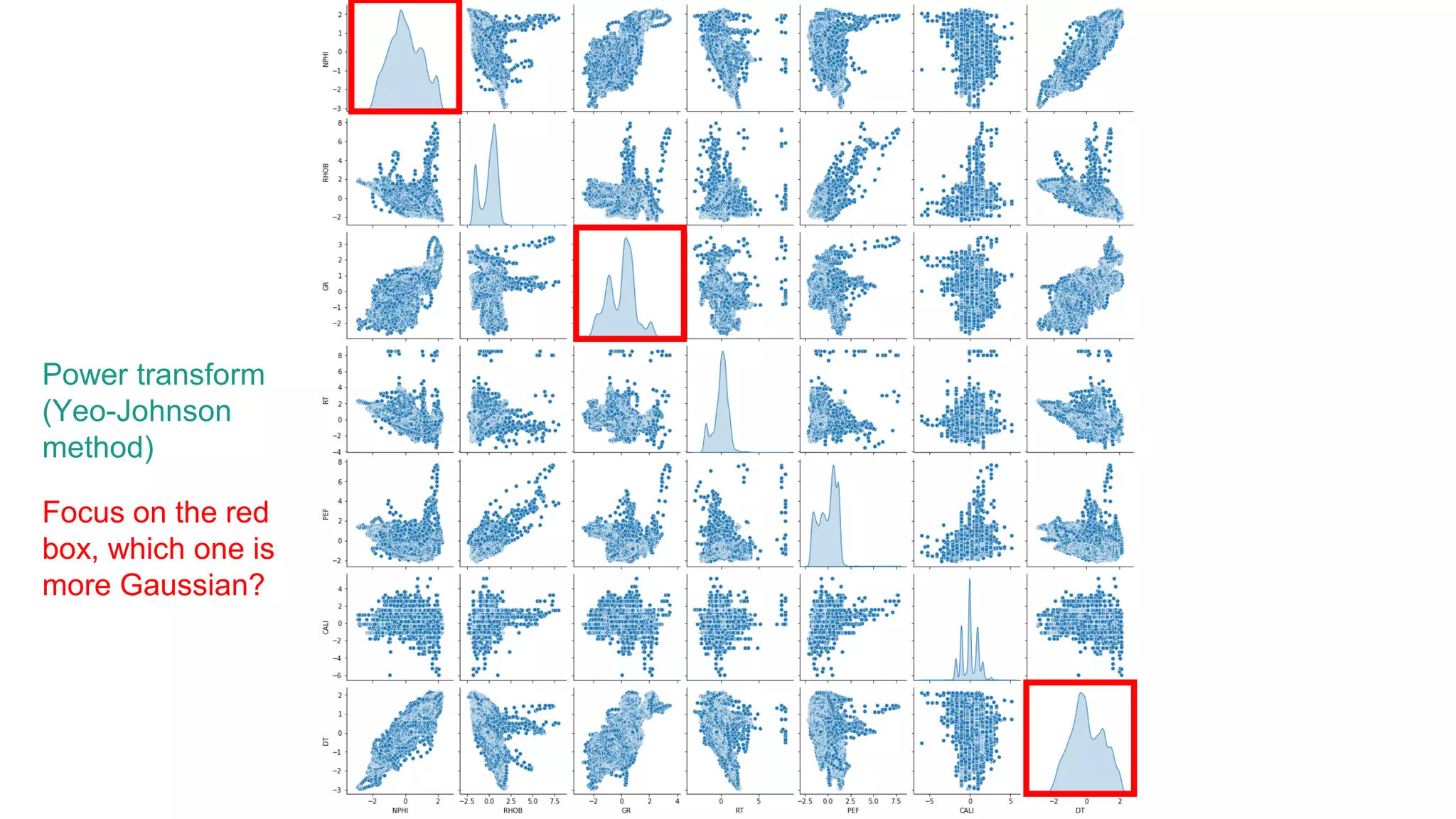
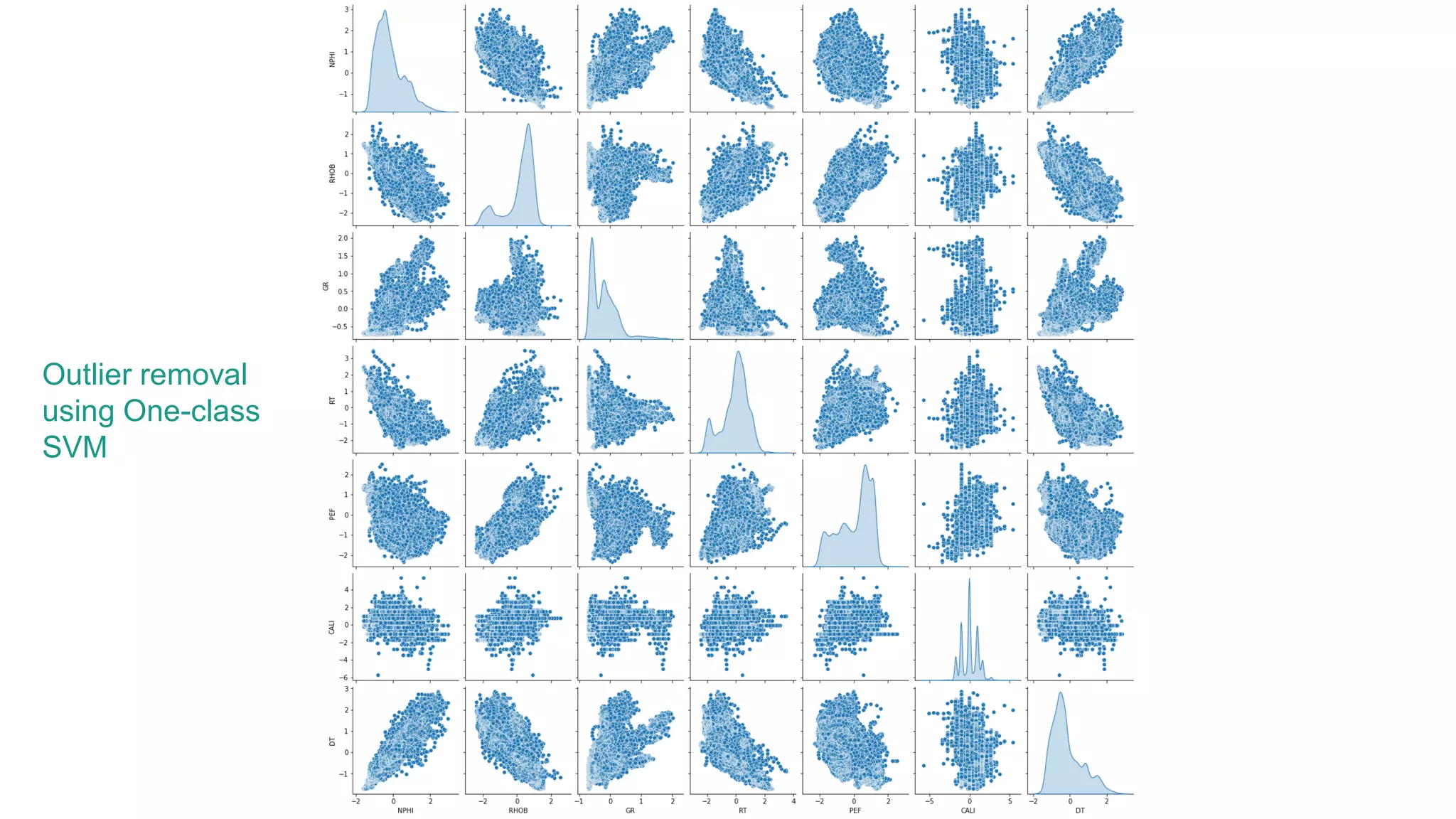
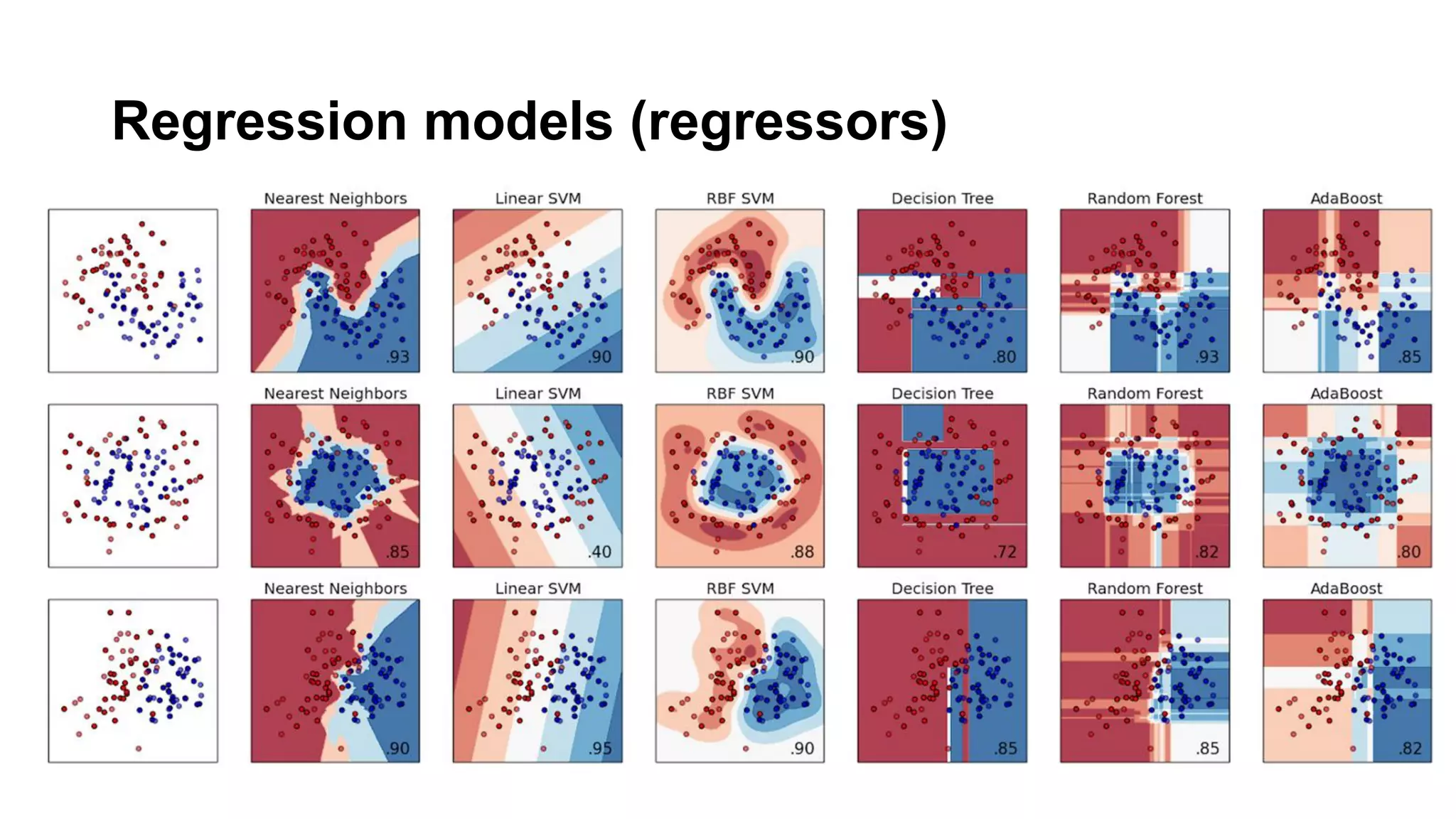
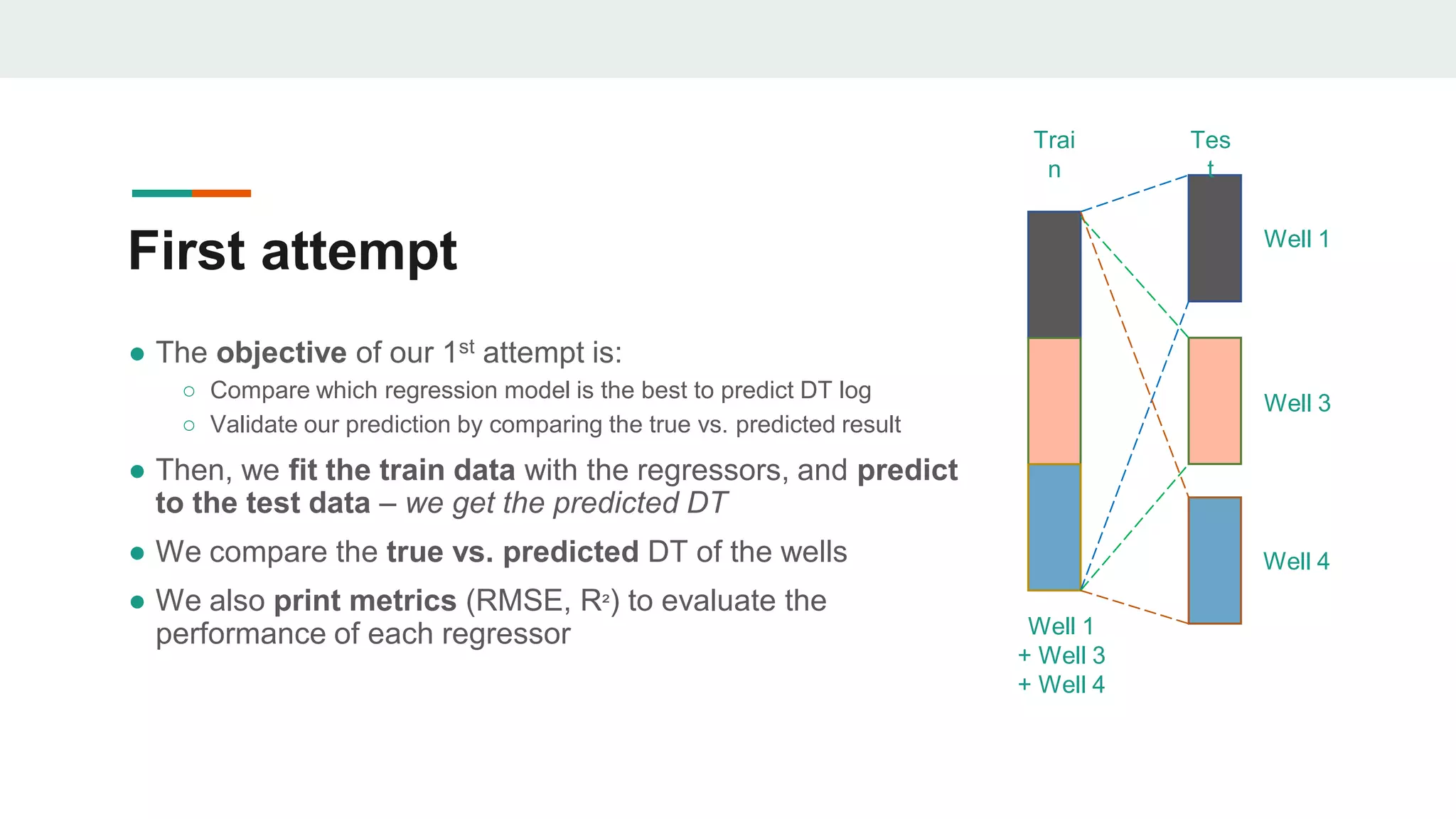
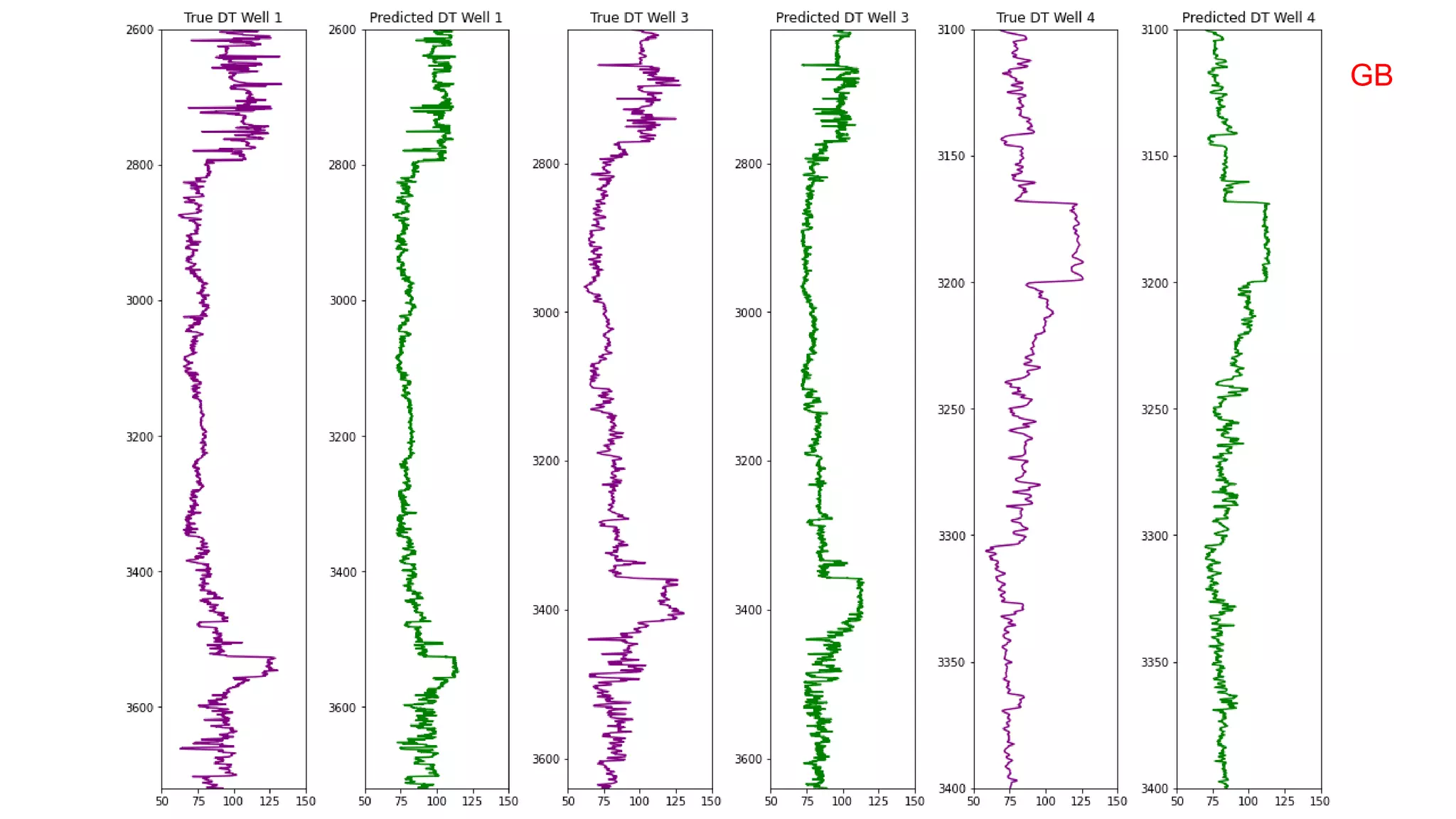
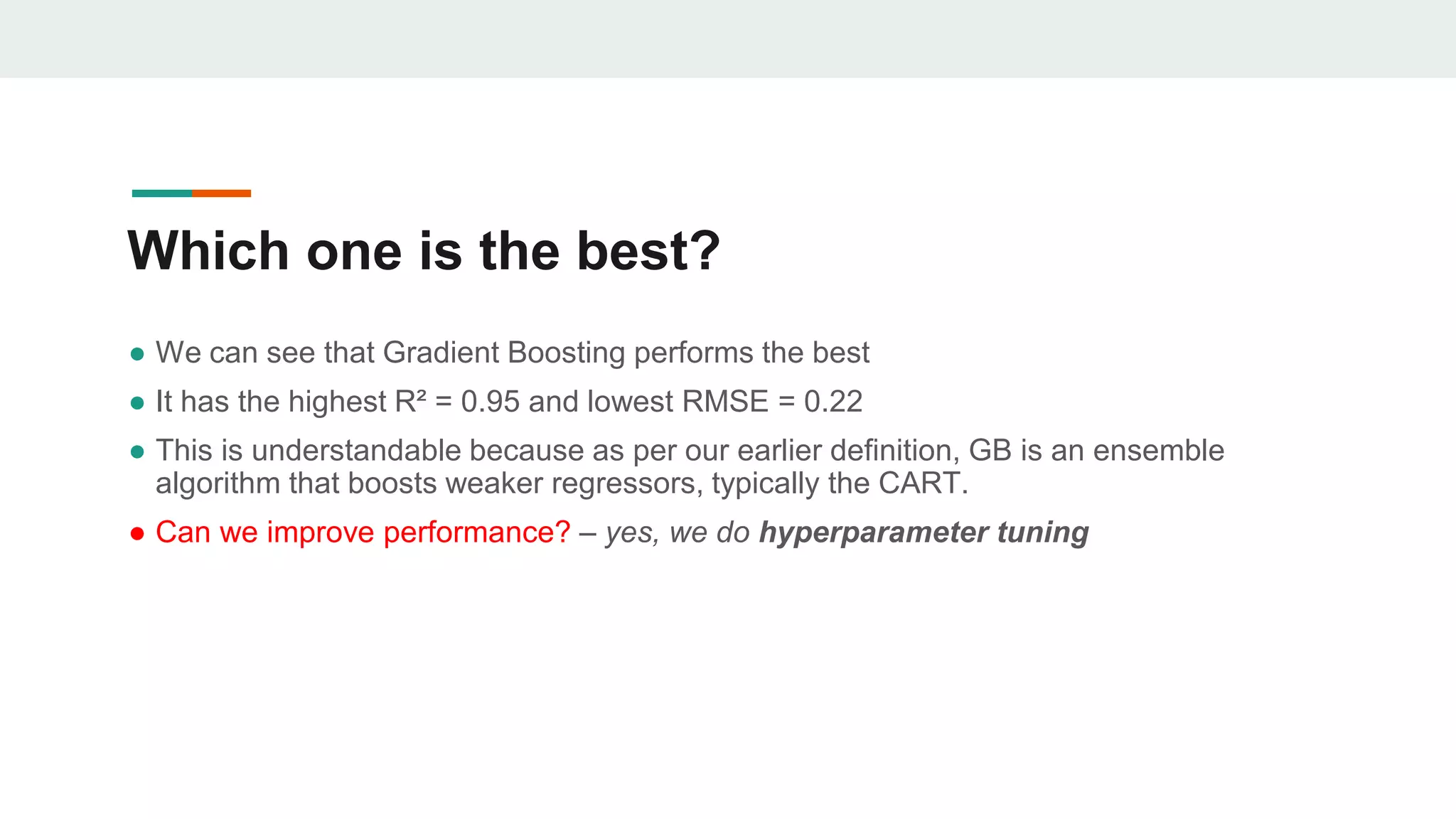
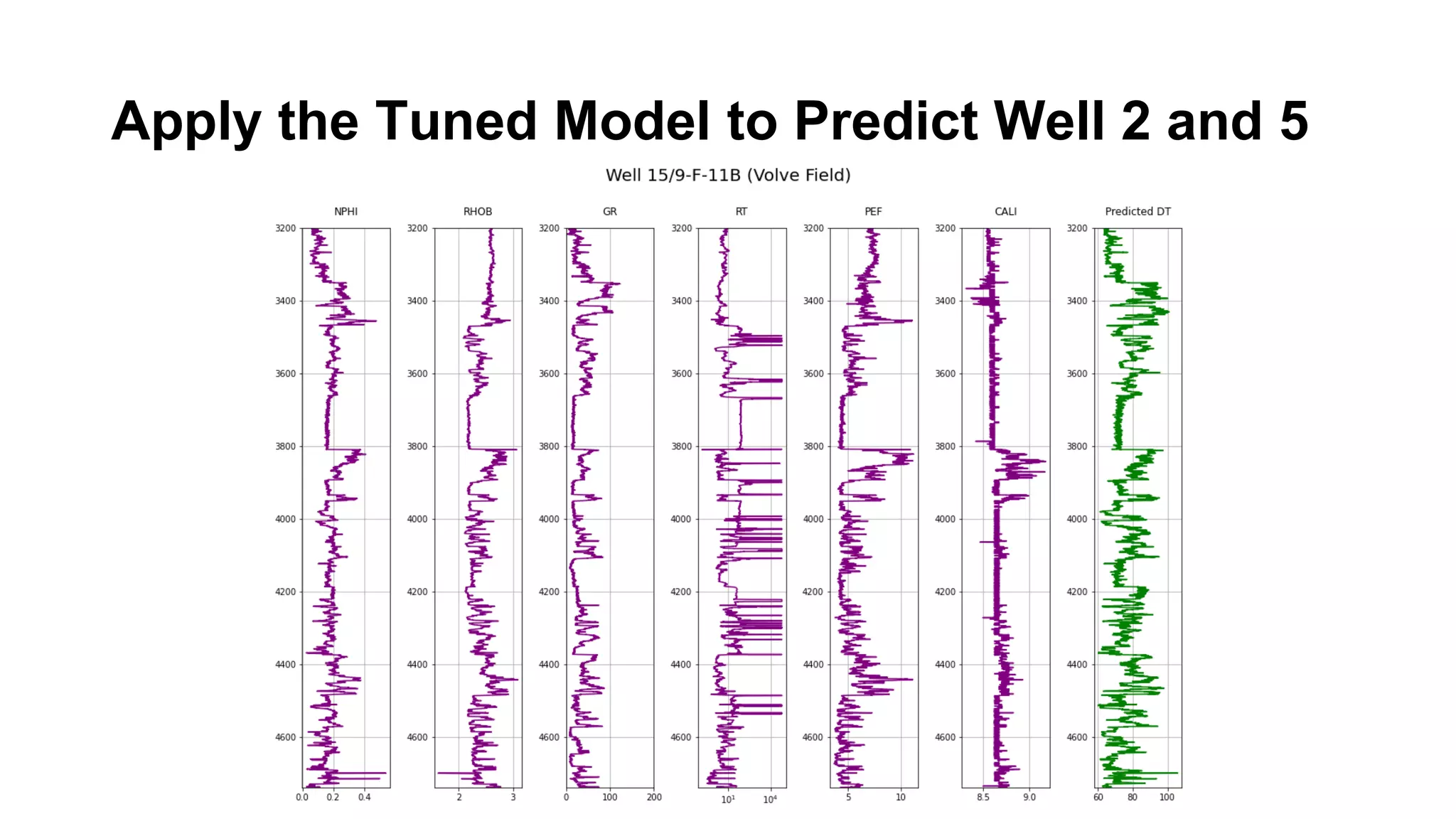
This document discusses the application of machine learning in subsurface analysis, focusing on a case study in the Volve field in the North Sea. It outlines the machine learning workflow and techniques for exploratory data analysis, feature engineering, and prediction using various regression models, concluding that gradient boosting performs the best in this context. The importance of data normalization and outlier removal is highlighted as critical steps for improving prediction accuracy.

1. Machine Learning Application in
Subsurface Analysis: Case Study in
the North Sea
Yohanes Nuwara
December 2, 2020
International Geosciences
Symposium

2. Outlines
● What is Machine Learning ?
● Machine learning in geoscience
● Machine learning workflow
● Case study in Volve field, North Sea
● Exploratory data analysis & Pre-processing
● Prediction
● Conclusion

3. What is Machine Learning?
● An algorithm-assisted process …
● … that learns through data (as an input),
● … train the data
● … to fit to a mathematical model,
● … and finally output a prediction
Source: Federated Learning (Google AI)

4. Solving Specific Problems in Geoscience with
ML
● Missing geophysical log traces – supervised learning prediction
● Generating facies model based on geophysical logs from the nearby wells –
supervised learning classification
● Clustering different facies – unsupervised learning classification
● Fault identification – supervised learning (Convolutional Neural Networks / CNN)
● Salt body (or other anomalies e.g. gas chimney) – supervised learning (CNN)
● Rock typing – unsupervised learning (Self Organizing Maps / SOM)

5. DT
Pred DT
60.2
52.3
51.8
75.2
80.1
49.8
62.1
True DT
60
50
50
70
80
50
60
Machine learning terminologies
● Classification
● Regression
● Training
● Testing
● Supervised
● Unsupervised
● Features
● Target
● Observations
● Continuous
● Categorical
● Non-numerical
values
● Accuracy
Density Resistivity Gamma Ray Formation
2.5 100 80 Heather
2.7 70 Heather
2.2 50 150 Hugin
50 30 Hugin
2.7 75 Hugin
2.2 50 150 Sleipner
50 30 Sleipner
75
55
2.3
2.3
Density Resistivity Gamma Ray Formation
2.5 100 80 Hugin
2.7 30 70 Hugin
2.2 50 150 Hugin
60.2
70.5
82.5

6. Exploratory Data
Analysis
Feature selection
Feature
engineering
Data normalization Removing outliers
Train-test split
1st training and
prediction
Metric of
each model
Hyperparameter
tuning
True vs
Predicted
Validation
Best hyper-
parameters
Final prediction
Final
predicted
result
Feature
and target
data

7. Overview of Volve Dataset

8. Data overview
● Volve field dataset is a massive volume of data released for public by Equinor in 2018
● There are data from 20+ wells, but only 5 are used for now
● 5 wells are: 15/9-F-11A, 15/9-F-11B, 15/9-F-1A, 15/9-F-1B, and 15/9-F-1C (just call them well
1, 2, 3, 4, and 5)
● Well 1, 3, and 4 have DT log; well 2 and 5 don’t have DT log
● Our objective now: use machine learning to predict DT log on well 2 and 5

9. Well 3 (train)

10. Well 5
(test)

11. EDA and Pre-processing

12. Exploratory Data Analysis 1 (Pairplot)
● Pairplot shows how the data is distributed among itself (univariate) and with one
another (multivariate)
● Diagonal shows the histogram OR “probability density function” (univariate)
● Non-diagonal shows the crossplot of one log and another (multivariate)

13. Diagonal is the
“probabilistic
density function”
Non-diagonal is the
crossplot between
logs
A
B
C
D
E
F
G
(A) NPHI shows a
left-skewed
distribution
(B) RT shows a
“spike” distribution
(C) Outliers can be
seen
(D) Positive
correlation between
DT and NPHI
(E) Positive
correlation between
RHOB and PEF
(F) Negative
correlation between
RHOB and DT
(G) Less correlation
between DT and
CALI

14. Exploratory Data Analysis 2 (Heatmap)
● Correlation heatmap shows the correlation between two variables (logs) in a visual way
● Calculate the correlation (2 kinds: Pearson or Spearman)
● Heatmap will tell which features should be phased out – two variables that have LOW
correlation shouldn’t be used as feature for prediction
Pearson’s
correlation
Spearman’s
correlation

16. Dealing with missing data
● Missing data (NaN; non-numerical value) will be a problem for ML
● 2 ways to handle the missing data:
○ Drop all observations (rows) that have NaN – if we have small dataset, this is not a suggested way
round
○ Impute the NaN with the mean value of the data – also called as imputation

17. Missing data of facies of 233 wells in the North Sea (below are the 25 wells)
GEOLINK data

18. Feature engineering
● Feature engineering is a way to transform a variable into a new feature using any
mathematical functions (e.g. log, exponent, etc.) – you can also create new features.
● In petrophysics we know that we’ll visualize RT better if we make it in a semilog plot
● Therefore, we can transform RT into log(RT)
● Then see the new feature using pairplot

19. Look at this RT now
is better distributed
(no spike anymore)

20. Data transformation
● Also known as feature scaling
● The objective is to make the distribution be more Gaussian – less skewed
● There are two basic ways: standardization and normalization
● Standardization 🡪 transforming the data by using its standard deviation and average
● Normalization 🡪 transforming the data by using its min and max value
● Other methods such as power transform (box-cox or Yeo-Johnson method) and
regularization (L1 and L2 norm)
● We need to compare which one is the best?

21. Standardization
(Std and mean)
Focus on the red
box, which one is
more Gaussian?

22. Power transform
(Yeo-Johnson
method)
Focus on the red
box, which one is
more Gaussian?

23. Outlier removal
● We saw many outliers in the data
● In fact, machine learning works better if outliers are minimized
● The most basic way to remove outliers is by restricting the data only within the std –
and outside the std, are outliers.
● There are lots of other methods: Isolation Forest, Minimum Covariance (elliptic
envelope method), Local Outlier Factor, and One-class SVM
● Again we compare which one is the best?

24. Outlier removal
using One-class
SVM

25. Prediction

26. Regression models (regressors)

27. First attempt
● The objective of our 1st attempt is:
○ Compare which regression model is the best to predict DT log
○ Validate our prediction by comparing the true vs. predicted result
● Then, we fit the train data with the regressors, and predict
to the test data – we get the predicted DT
● We compare the true vs. predicted DT of the wells
● We also print metrics (RMSE, R²) to evaluate the
performance of each regressor Well 1
+ Well 3
+ Well 4
Well 1
Well 3
Well 4
Trai
n
Tes
t

28. Linear regression
SVM
Random Forest
Decision tree
Gradient Boosting
K-Nearest Neighbor

29. GB

30. Which one is the best?
● We can see that Gradient Boosting performs the best
● It has the highest R² = 0.95 and lowest RMSE = 0.22
● This is understandable because as per our earlier definition, GB is an ensemble
algorithm that boosts weaker regressors, typically the CART.
● Can we improve performance? – yes, we do hyperparameter tuning

31. Hyperparameter Tuning
● An optimization algorithm to search the best hyperparameters for the regressor we use
to optimize the prediction.
● What is hyperparameters – they are variables that we use for the regressors to predict,
that is independent of our data
● Example of hyperparameters – K value in KNN, learning rate in neural network
● We use grid search CV
Without tuned hyperparameters (default) With tuned hyperparameters

32. Apply the Tuned Model to Predict Well 2 and 5

33. ● Three wells in the Volve field (F11A, F1A, and F1B) are trained to predict two wells
(F11B and F1C) that don’t have P-sonic log
● Data normalization and removing outliers are critical step in machine learning
● The best performing regressor is Gradient Boosting
● Hyperparameter tuning are useful to find the best hyperparameters for regressor
(although takes more time)
Conclusion

34. Thank you
Want to discuss?
E-mail : ign.nuwara97@gmail.com
LinkedIn : https://www.linkedin.com/in/yohanesnuwara/