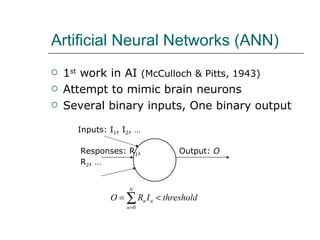
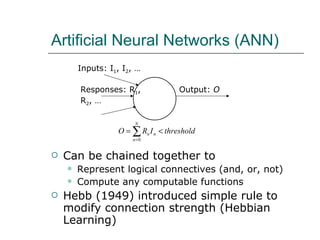
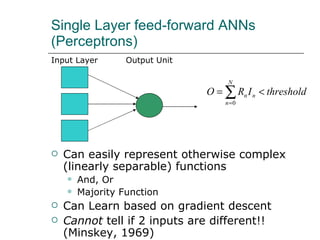
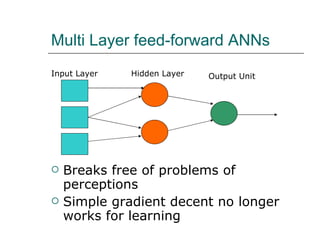
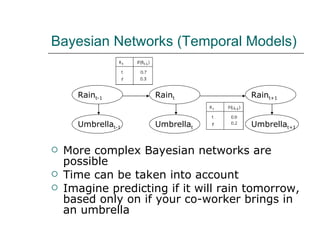
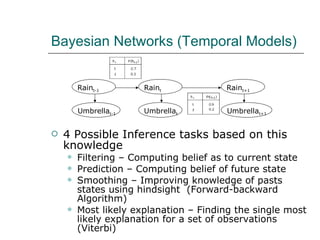
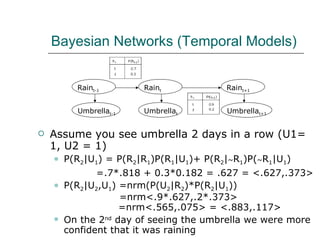
1. The document discusses different approaches to knowledge representation and machine learning including first order logic, artificial neural networks, Bayesian networks, and reinforcement learning. 2. Artificial neural networks can represent complex functions by learning through backpropagation but lack interpretability, while Bayesian networks combine logic and learning from experience under uncertainty. 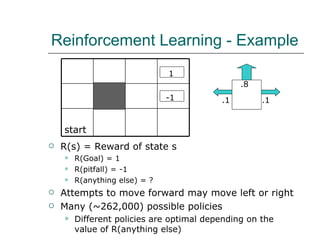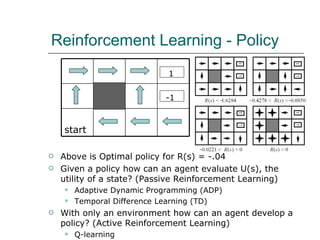3. Reinforcement learning defines rewards and punishments to allow agents to discover optimal policies without being explicitly programmed through interactions with an environment.

1. Knowledge Representation and Machine Learning Stephen J. Guy

2. Overview Recap some Knowledge Rep. History First order logic Machine Learning ANN Bayesian Networks Reinforcement Learning Summary

3. Knowledge Representation? Ambiguous term “ The study of how to put knowledge into a form that a computer can reason with” (Russell and Norvig) Originally couple w/ linguistics Lead to philosophical analysis of language

4. Knowledge Representation? Cool Robots Futuristic Robots

5. Early Work Blockworlds (1972) SHRDLU “ Find a block which is taller than the one you are holding and put it in the box” SAINT (1963) Closed form Calculus Problems STUDENT (1967) “ If the number of customers Tom gets is twice the square of 20% of the number of advertisements he runs, and the number of advertisements he runs is 45, what is the number of customers Tom gets?

6. Early Work - Theme Limit domain “ Microworlds” Allows precise rules Generality Problem Size 1) Making rules are hard 2) State space is unbounded

7. Generality First-order Logic Is able to capture simple Boolean relations and facts  x  y Brother(x,y)  Sibling(x,y)  x  y Loves(x,y) Can capture lots of commonsense knowledge Not a cure-all

8. First order Logic - Problems Faithful captures fact, objects and relations Problems Does not capture temporal relations Does not handle probabilistic facts Does not handle facts w/ degrees of truth Has been extended to: Temporal logic Probability theory Fuzzy logic

9. First order Logic - Bigger Problem Still lots of human effort “Knowledge Engineering” Time consuming Difficult to debug Size still a problem Automated acquisition of knowledge is important

10. Machine Learning Sidesteps all of the previous problems Represent Knowledge in a way that is immediately useful for decision making 3 specific examples Artificial Neural Networks (ANN) Bayesian Networks Reinforcement Learning

11. Artificial Neural Networks (ANN) 1 st work in AI (McCulloch & Pitts, 1943) Attempt to mimic brain neurons Several binary inputs, One binary output Inputs: I 1 , I 2 , … Output: O Responses: R 1 , R 2 , …

12. Artificial Neural Networks (ANN) Can be chained together to Represent logical connectives (and, or, not) Compute any computable functions Hebb (1949) introduced simple rule to modify connection strength (Hebbian Learning) Inputs: I 1 , I 2 , … Output: O Responses: R 1 , R 2 , …

13. Single Layer feed-forward ANNs (Perceptrons) Input Layer Output Unit Can easily represent otherwise complex (linearly separable) functions And, Or Majority Function Can Learn based on gradient descent Cannot tell if 2 inputs are different!! (Minskey, 1969)

14. Learning in Perceptrons Replace Threshold function w/ Sigmod g(x) Define Error Metric (Sum Sqr Diff) Calculate Gradient wrt Weight Err * g’(in) * X j W j = W j +  * Err * g’(in) * X j

15. Multi Layer feed-forward ANNs Breaks free of problems of perceptions Simple gradient decent no longer works for learning Input Layer Output Unit Hidden Layer

16. Learning in Multilayer ANNs (1/2) Backpropagation Treat top level just like single-layer ANN Diffuse error down network based on input strength from each hidden node

17. Learning in Multilayer ANNs (2/2)  i = Err i * g’(in i ) W j,i = W j,i +  * a j *  i W k,j = W k,j +  * a k *  j

18. ANN - Summery Single Layer ANNs (Proceptrons) can capture linearly separable functions Multi-layer ANNs can caputer much more complex functions and can be effectively trained using back-propagation Not a silver bullet How to avoid over-fitting? What shape should the network be? Network values are meaningless to humans

19. ANN – In Robots (Simple) Can be easily set up and robot Brian Input = Sensors Output = Motor Control Simple Robot learns to avoid bumps

20. ANN – In Robots (Complex) Autonomous Land Vehicle In a Neural Network (ALVINN) CMU project learned to drive from humans 32x30 “retina” 5 hidden layers 30 output nodes Capable of driving itself after 2-3 minutes of training

21. Bayesian Networks Combines advantages of basic logic and ANNs Allows for “effucient represenation of, and rigorous reasoning with, unceartain knwoledge” (R&N) Allows for learning from experience

22. Bayes’ Rule P(b|a) = P(a|b)*P(b)/P(a) = nrm(<P(a|b)*P(b), P(a|~b)*P(~b)>) Meningitis Example (From R&N) s=stiff neck, m = has meningitis P(s|m) = 0.5 P(m) = 1/50000 P(s) = 1/20 P(m|s) = P(s|m)P(m)/P(s) = .5*(1/5000)/(1/2) = .0002 Diagnostic knowledge more fragile than causal knowledge

23. Bayesian Networks Allows us to chain together more complex relations Creating network is not necessarily easy Create a fully connected network Cluster groups w/ high correlation together Find probabilities using rejection sampling P(M) = 1/50000 M P(S) T .5 F 1/20 Meningitis Stiff Neck

24. Bayesian Networks (Temporal Models) More complex Bayesian networks are possible Time can be taken into account Imagine predicting if it will rain tomorrow, based only on if your co-worker brings in an umbrella Rain t-1 Umbrella t-1 Rain t Umbrella t Rain t+1 Umbrella t+1

25. Bayesian Networks (Temporal Models) 4 Possible Inference tasks based on this knowledge Filtering – Computing belief as to current state Prediction – Computing belief of future state Smoothing – Improving knowledge of pasts states using hindsight (Forward-backward Algorithm) Most likely explanation – Finding the single most likely explanation for a set of observations (Viterbi) Rain t-1 Umbrella t-1 Rain t Umbrella t Rain t+1 Umbrella t+1

26. Bayesian Networks (Temporal Models) Assume you see umbrella 2 days in a row (U 1 = 1, U 2 = 1) P(R 0 ) = <0.5,0.5> ( <.5 R 0 = T, .5 R 0 = F> ) P(R 1 ) = P(R 1 |R 0 )*P(R 0 )+P(R 1 | ~ R 0 )*P( ~ R 0 ) = 0.7*0.5 + 0.3*0.5 = <0.5,0.5> P(R 1 |U 1 ) =nrm(P(U 1 |R 1 )*P(R 1 )) =nrm<.9*.5,.3*.5> =nrm<.45,.1> = <.818,.182> Rain t-1 Umbrella t-1 Rain t Umbrella t Rain t+1 Umbrella t+1

27. Bayesian Networks (Temporal Models) Assume you see umbrella 2 days in a row (U1= 1, U2 = 1) P(R 2 |U 1 ) = P(R 2 |R 1 )P(R 1 |U 1 )+ P(R 2 | ~ R 1 )P( ~ R 1 |U 1 ) =.7*.818 + 0.3*0.182 = .627 = <.627,.373> P(R 2 |U 2 ,U 1 ) =nrm(P(U 2 |R 2 )*P(R 2 |U 1 )) =nrm<.9*.627,.2*.373> =nrm<.565,.075> = <.883,.117> On the 2 nd day of seeing the umbrella we were more confident that it was raining Rain t-1 Umbrella t-1 Rain t Umbrella t Rain t+1 Umbrella t+1

28. Bayesian Networks - Summary Bayesian Networks are able to capture some important aspects of human Knowledge Representation and use Uncertainty Adaptation Still difficulties in network design Overall a powerful tool Meaningful values in network Probabilistic logical reasoning

29. Bayesian Networks in Robotics Speech Recognition Inference Sensors Computer Vision SLAM Estimating Human Poses Robot going through doorway using Bayesian networks (Univ. of Basque)

30. Reinforcement Learning How much can we take the human out of loop? How do humans/animals do it? Genes Pain Pleasure Simply define rewards/punishments let agent figure out all the rest

31. Reinforcement Learning - Example R(s) = Reward of state s R(Goal) = 1 R(pitfall) = -1 R(anything else) = ? Attempts to move forward may move left or right Many (~262,000) possible policies Different policies are optimal depending on the value of R(anything else) start -1 1 .1 .1 .8

32. Reinforcement Learning - Policy Above is Optimal policy for R(s) = -.04 Given a policy how can an agent evaluate U(s), the utility of a state? (Passive Reinforcement Learning) Adaptive Dynamic Programming (ADP) Temporal Difference Learning (TD) With only an environment how can an agent develop a policy? (Active Reinforcement Learning) Q-learning start -1 1

33. Reinforcement Learning - Utility U(s) = R(s) +  U(s’)P(s’) ADP: Updating all U(s) based on each new observation TD: Update U(s) only for last state change Ideally: U(s) = R(s) + U(s’), but s’ is probabilistic U(s) = U(s) +  (R(s)+U(s’)-U(s))  decays from 1 to 0 as a function of # times state is visited U(s) is guaranteed converge to correct value 1 2 3 1 2 3 4 S’ 1 2 3 1 2 3 4

34. Reinforcement Learning – Policy Ideally Agents can create their own policies Exploration: Agents must be rewarded for exploring as well as taking best known path Adaptive Dynamic Programming (ADP) Can be achieved by changing U(s) to U’(s) U’(s) = n< N ? Max_Reward : U(s) Agent must also update transition model Temporal Difference Learning (TD) No changes to utility calculation! Can explore based on balancing utility and novelty (like ADP) Can chose random directions with a decreasing rate over time Both converge on optimal value

35. Reinforcement Learning in Robotics Robot Control Discretize workspace Policy Search Pegasus System (Ng, Stanford) Learned how to control robots Better than human pilots w/ Remote Control

36. Summary 3 different general learning approaches Artificial Neural Networks Good for learning correlation between inputs and outputs Little human work Bayesian Networks Good for handling uncertainty and noise Human work optional Reinforcement Learning Good for evaluating and generating policies/behaviors Can handle complex tasks Little human work

37. References 1. Russell S, Norvig P (1995) Artificial Intelligence: A Modern Approach , Prentice Hall Series in Artificial Intelligence. Englewood Cliffs, New Jersey ( http://aima.cs.berkeley.edu/ ) 2. Mitchell, Thomas. Machine Learning. McGraw Hill, 1997. ( http://www.cs.cmu.edu/~tom/mlbook.html ) 3. Sutton, Richard S., and Andrew G. Barto. Reinforcement Learning. Cambridge, MA: MIT Press, 1998.( http://www.cs.ualberta.ca/~sutton/book/the-book.html ) 4. Hecht-Nielsen, R. &quot;Theory of the backpropagation neural network.&quot; Neural Networks 1 (1989): 593-605. ( http://ieeexplore.ieee.org/xpls/abs_all.jsp?isnumber=3401&arnumber=118638 ) 5. P. Batavia, D. Pomerleau, and C. Thorpe, Tech. report CMU-RI-TR-96-31, Robotics Institute, Carnegie Mellon University, October, 1996 ( http://www.ri.cmu.edu/projects/project_160.html ) 6. Bayesian Network based Human Pose Estimation D.J. Jung, K.S. Kwon, and H.J. Kim (Korea) ( http:// www.actapress.com/PaperInfo.aspx?PaperID =23199 ) 7. Frank L. Lewis, &quot;Neural Network Control of Robot Manipulators,&quot; IEEE Expert: Intelligent Systems and Their Applications ,vol. 11, no. 3, pp. 64-75, June, 1996. ( http://doi.ieeecomputersociety.org/10.1109/64.506755 )