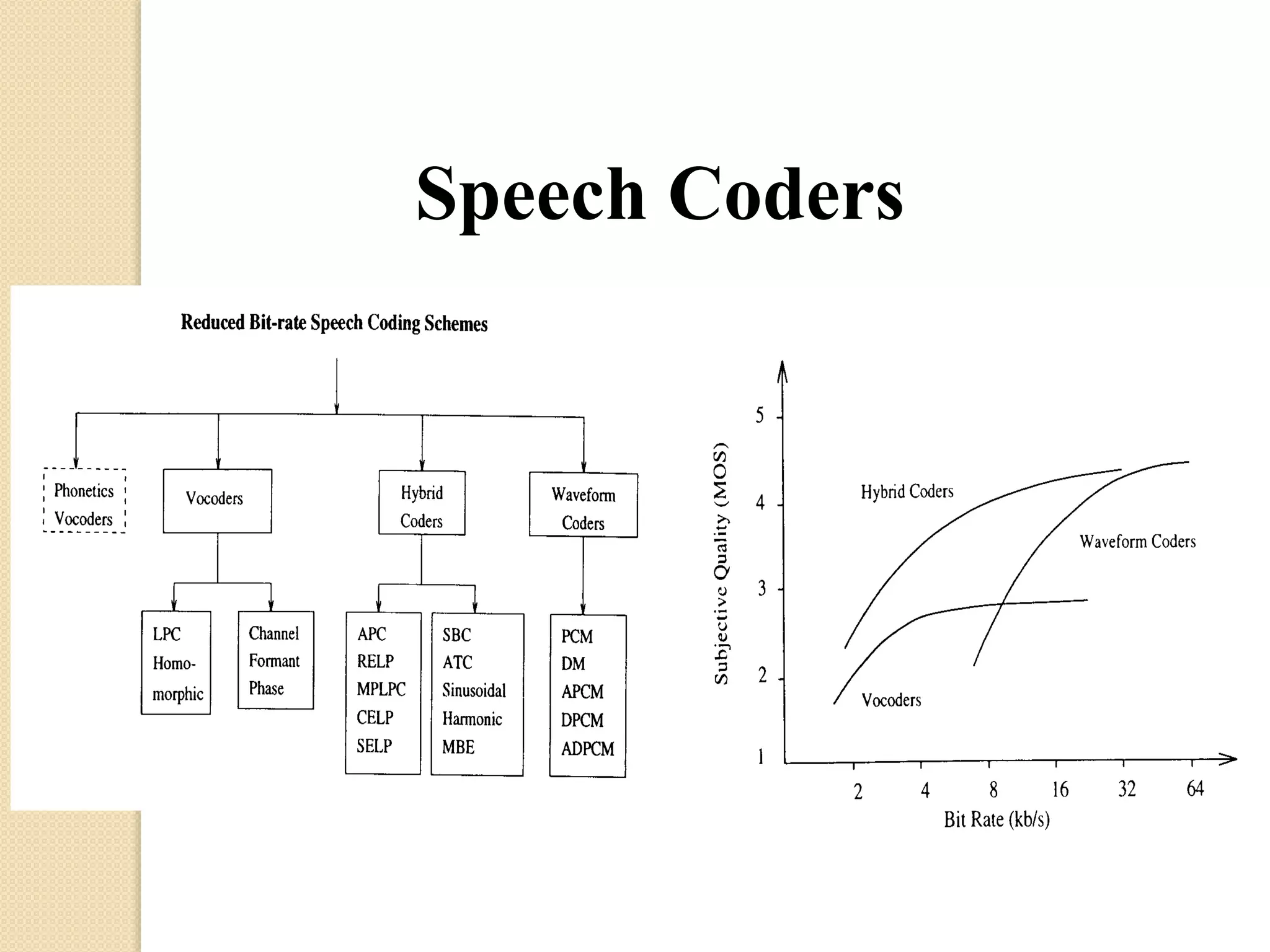
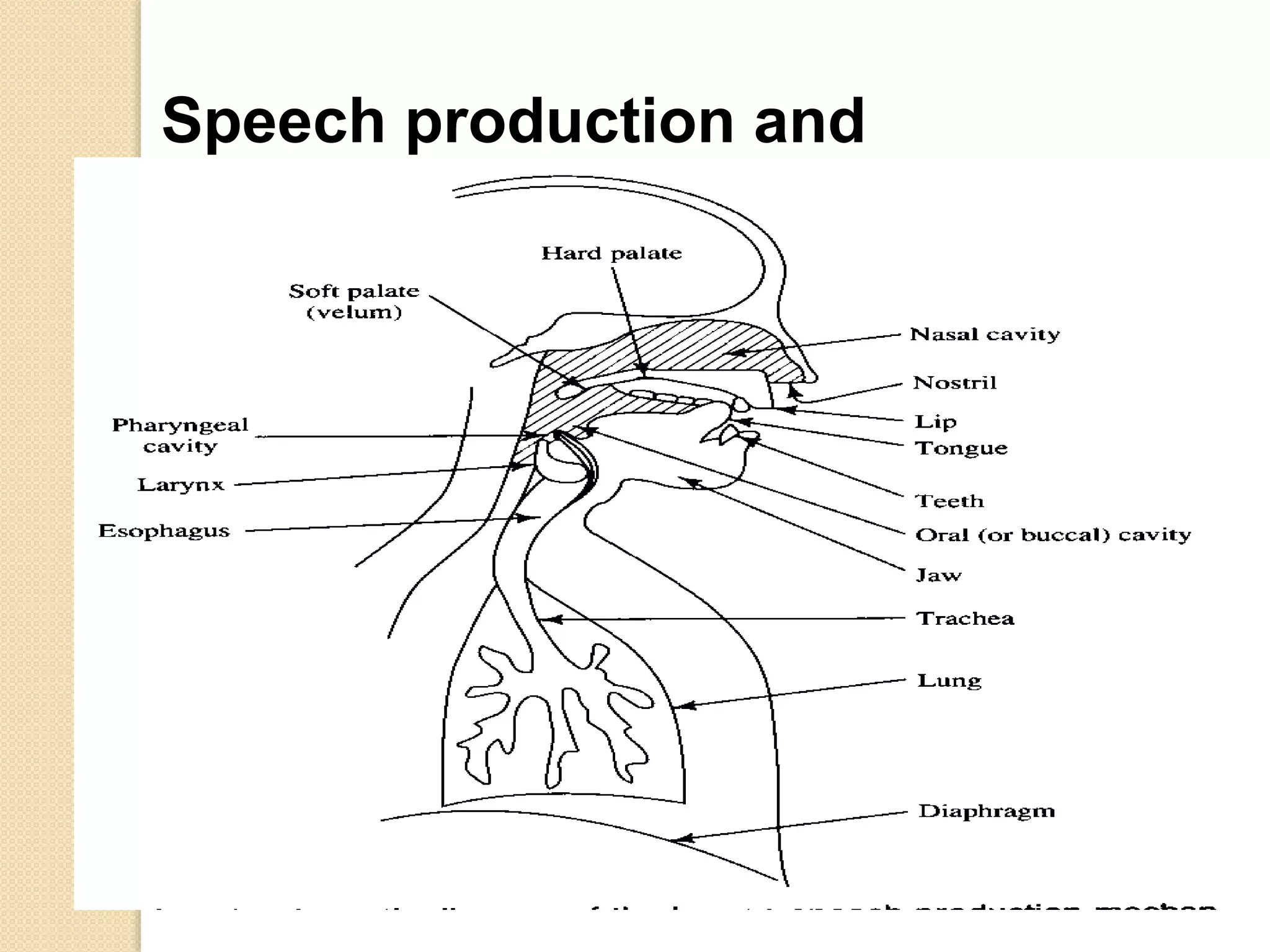
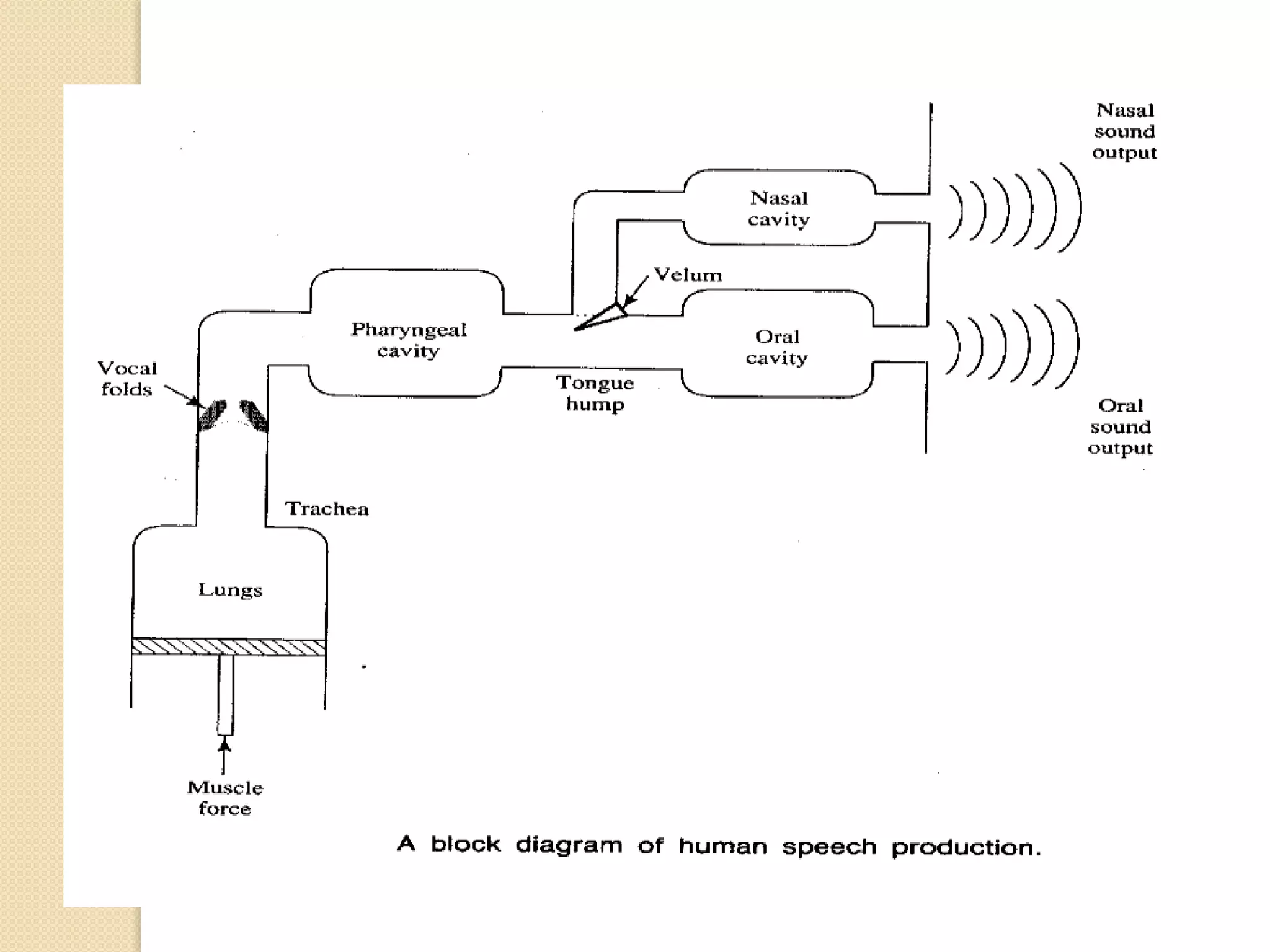
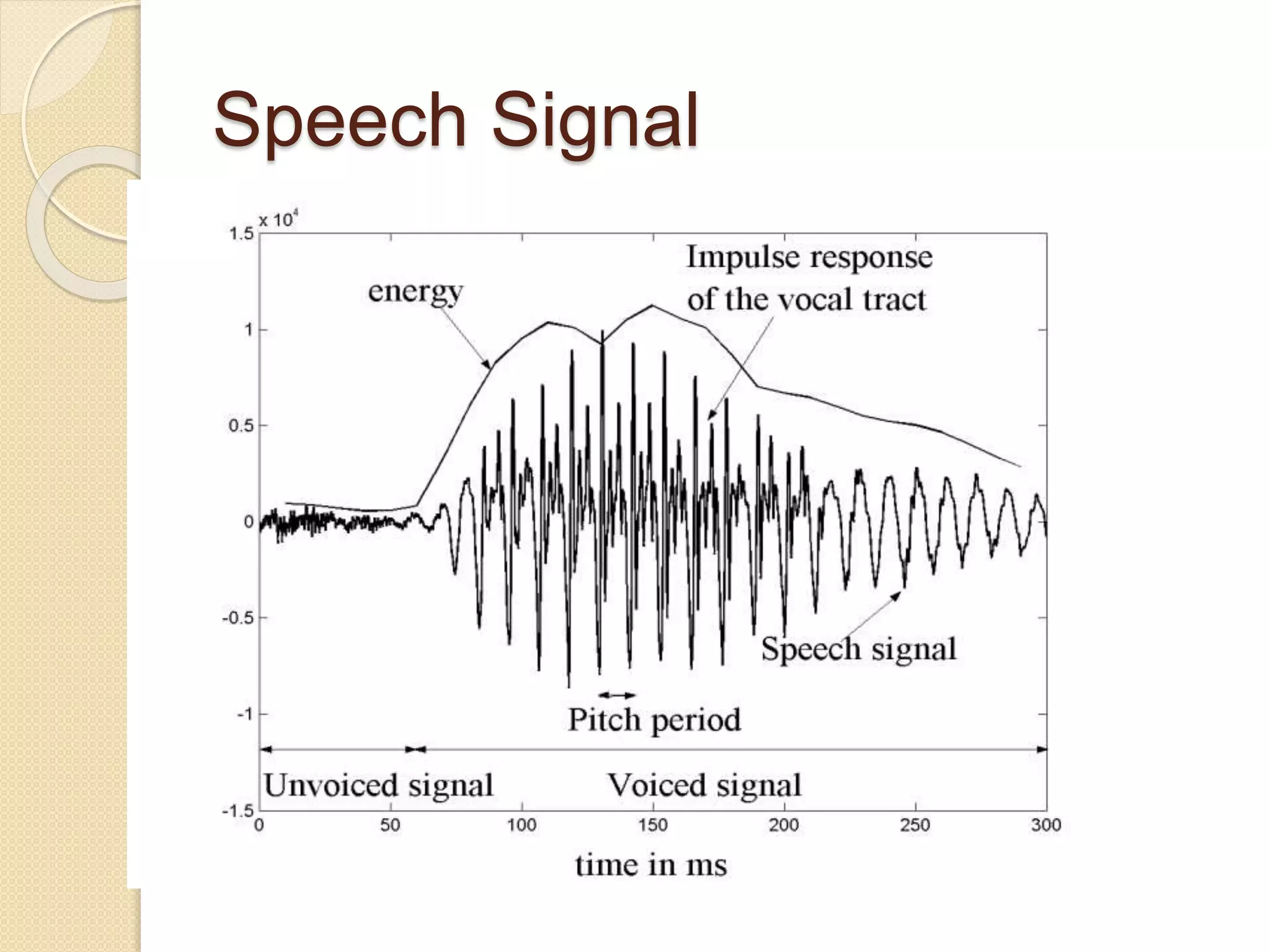
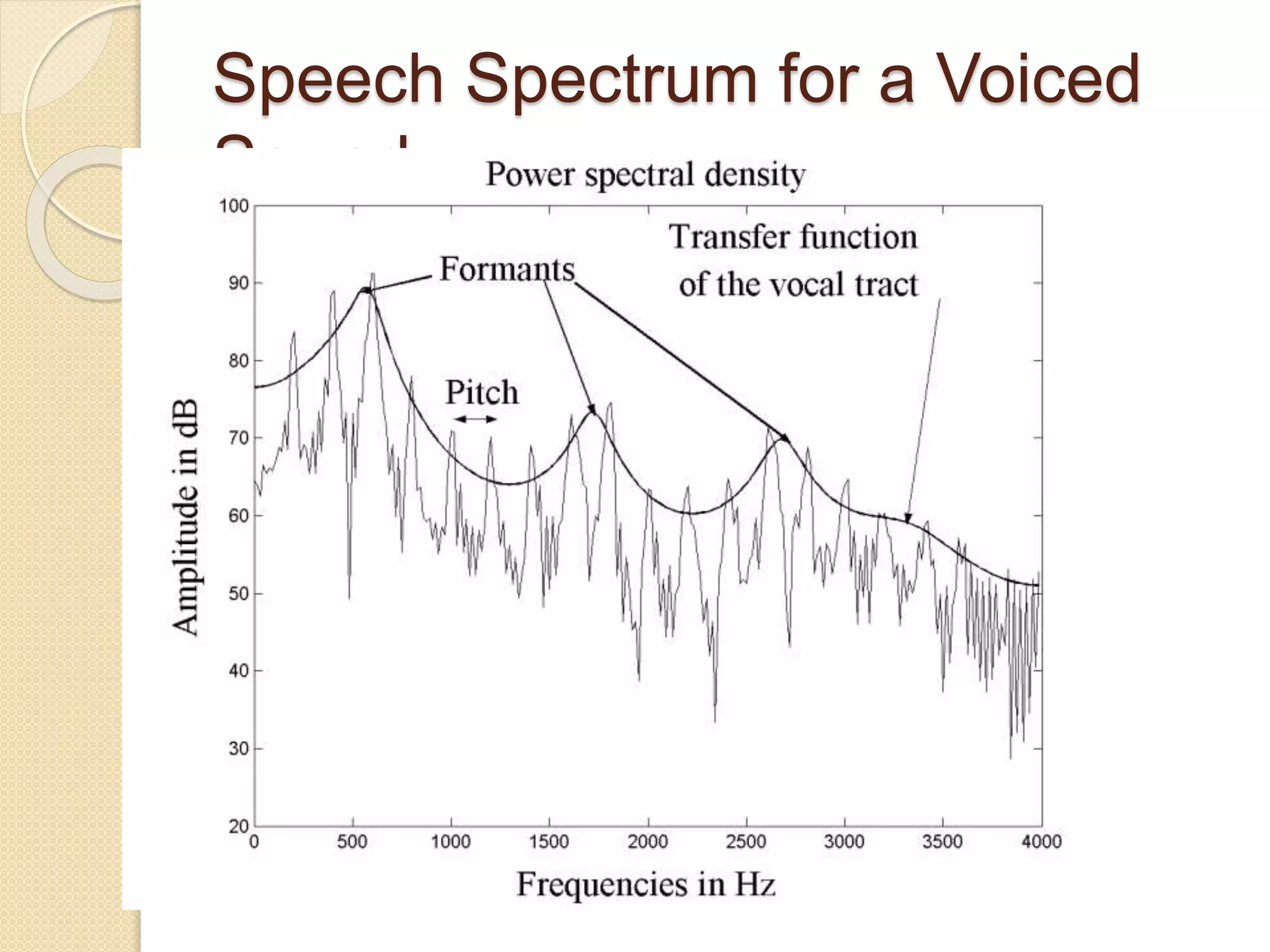
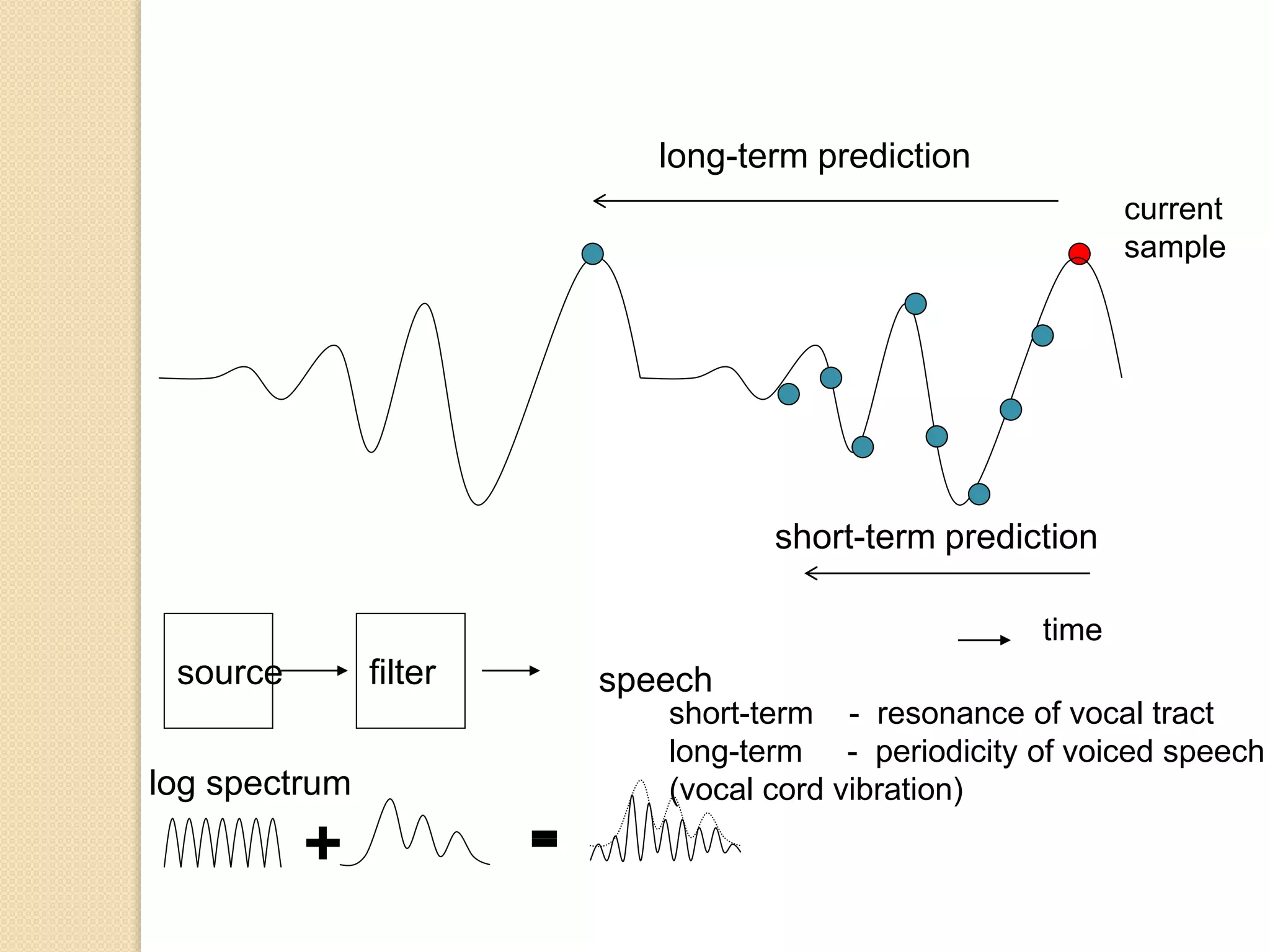
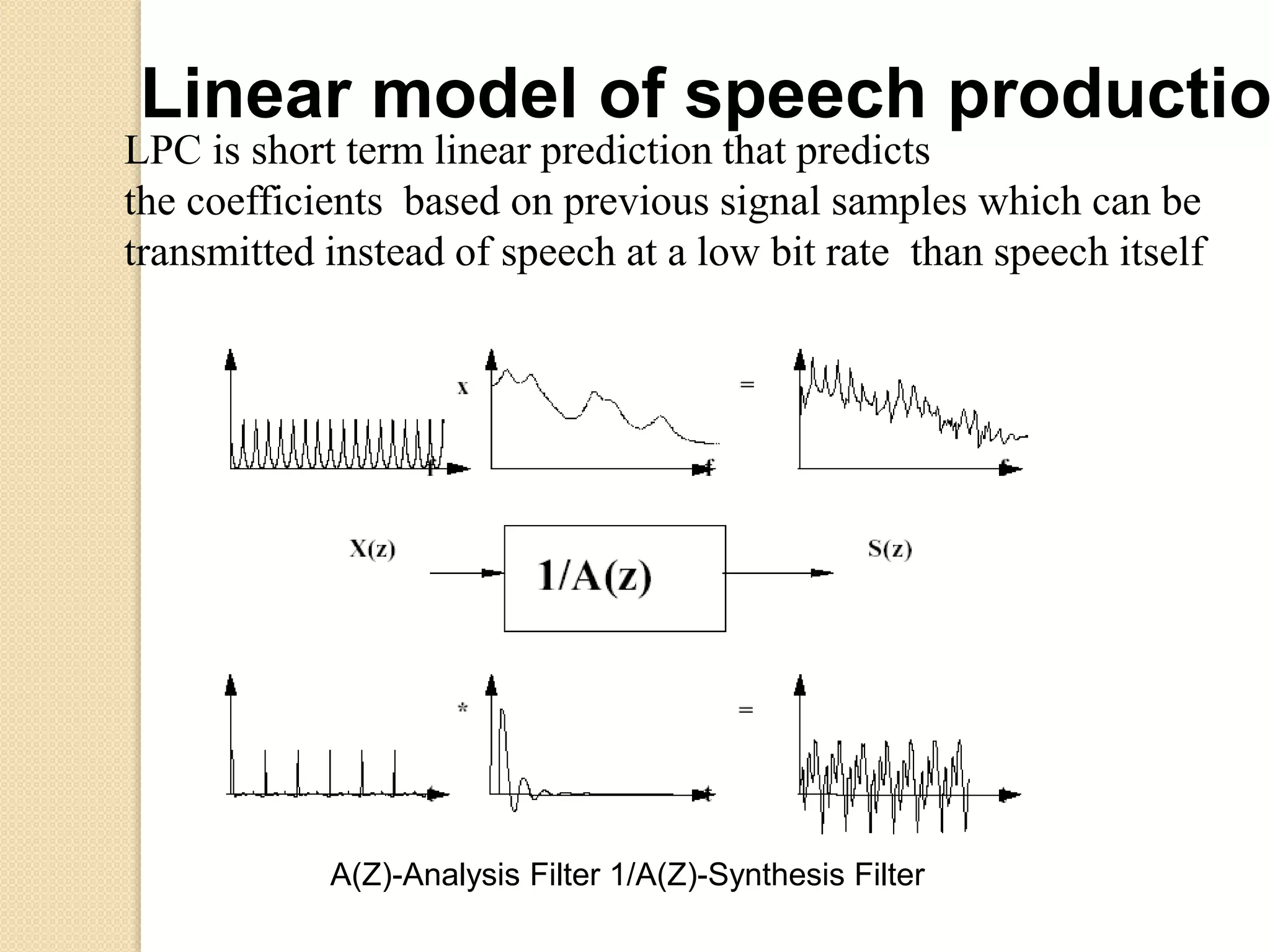
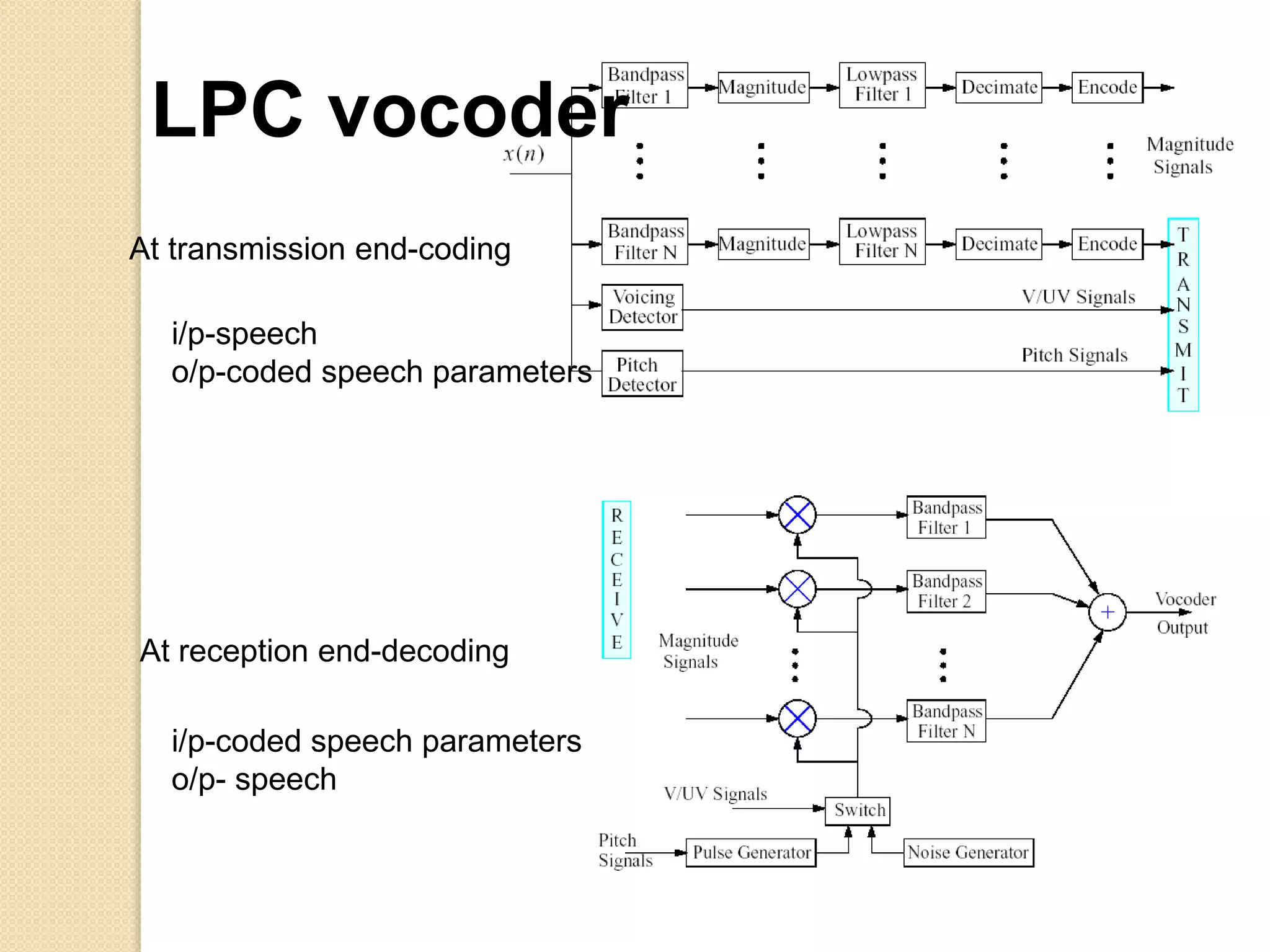
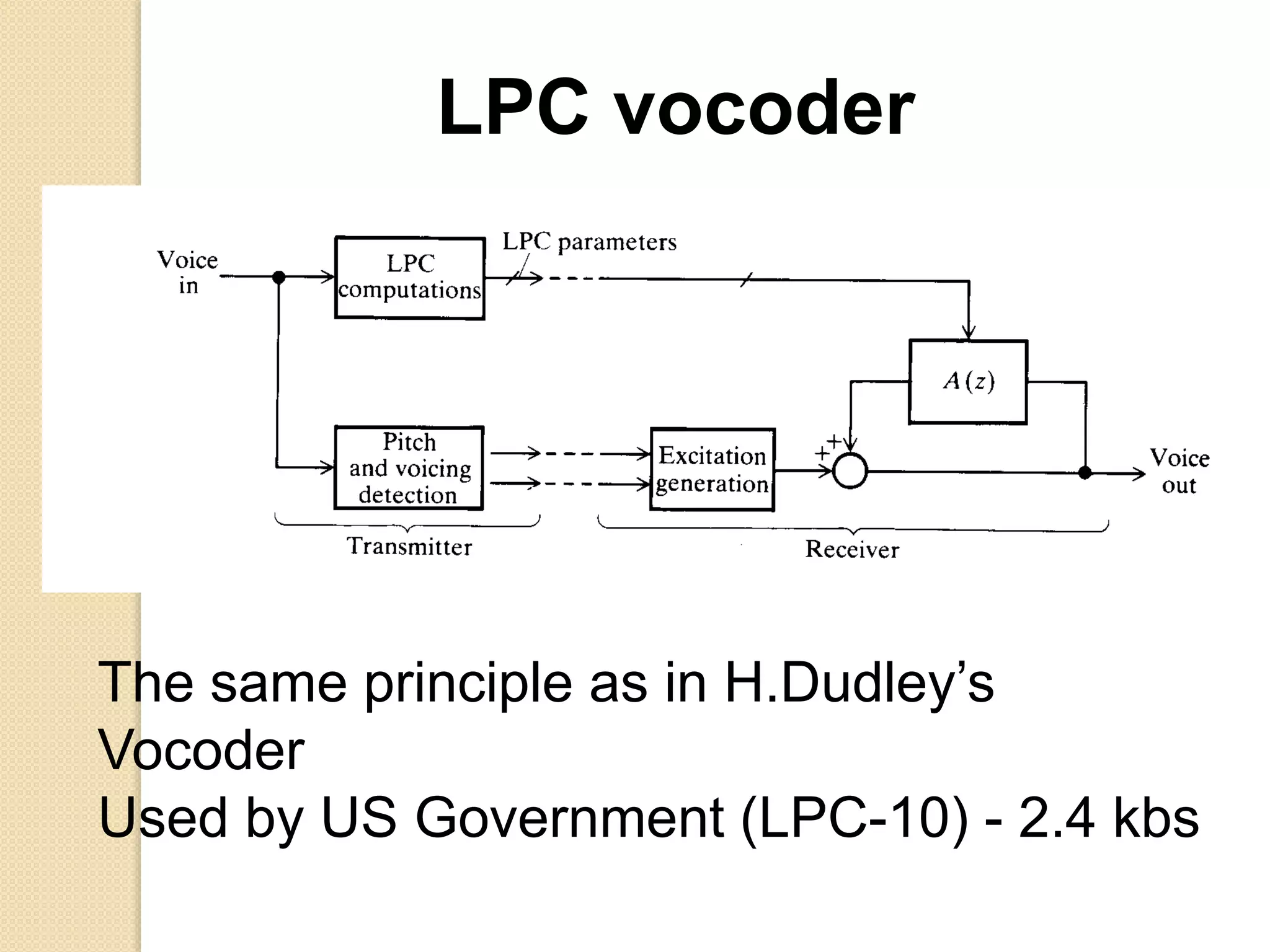
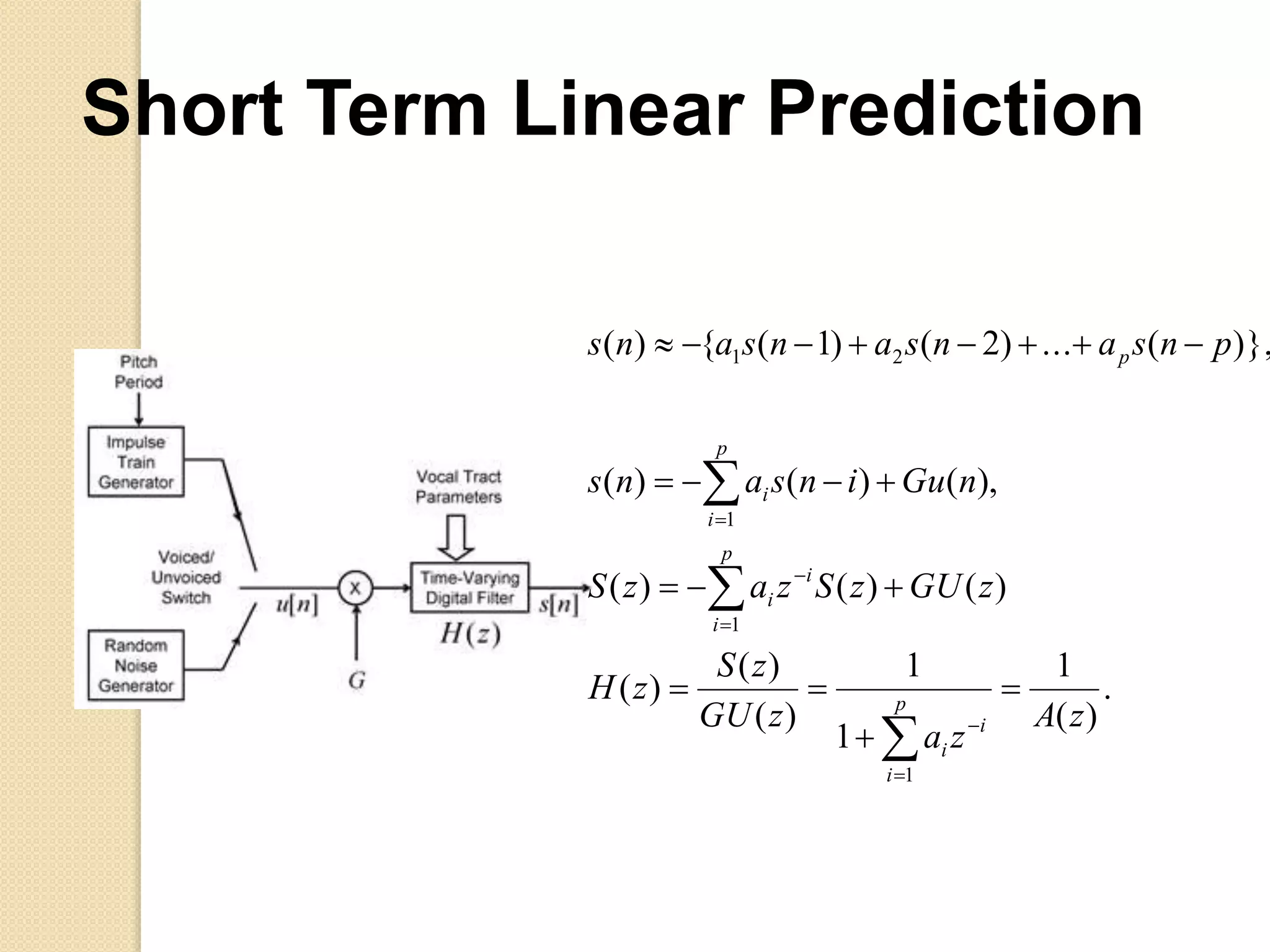
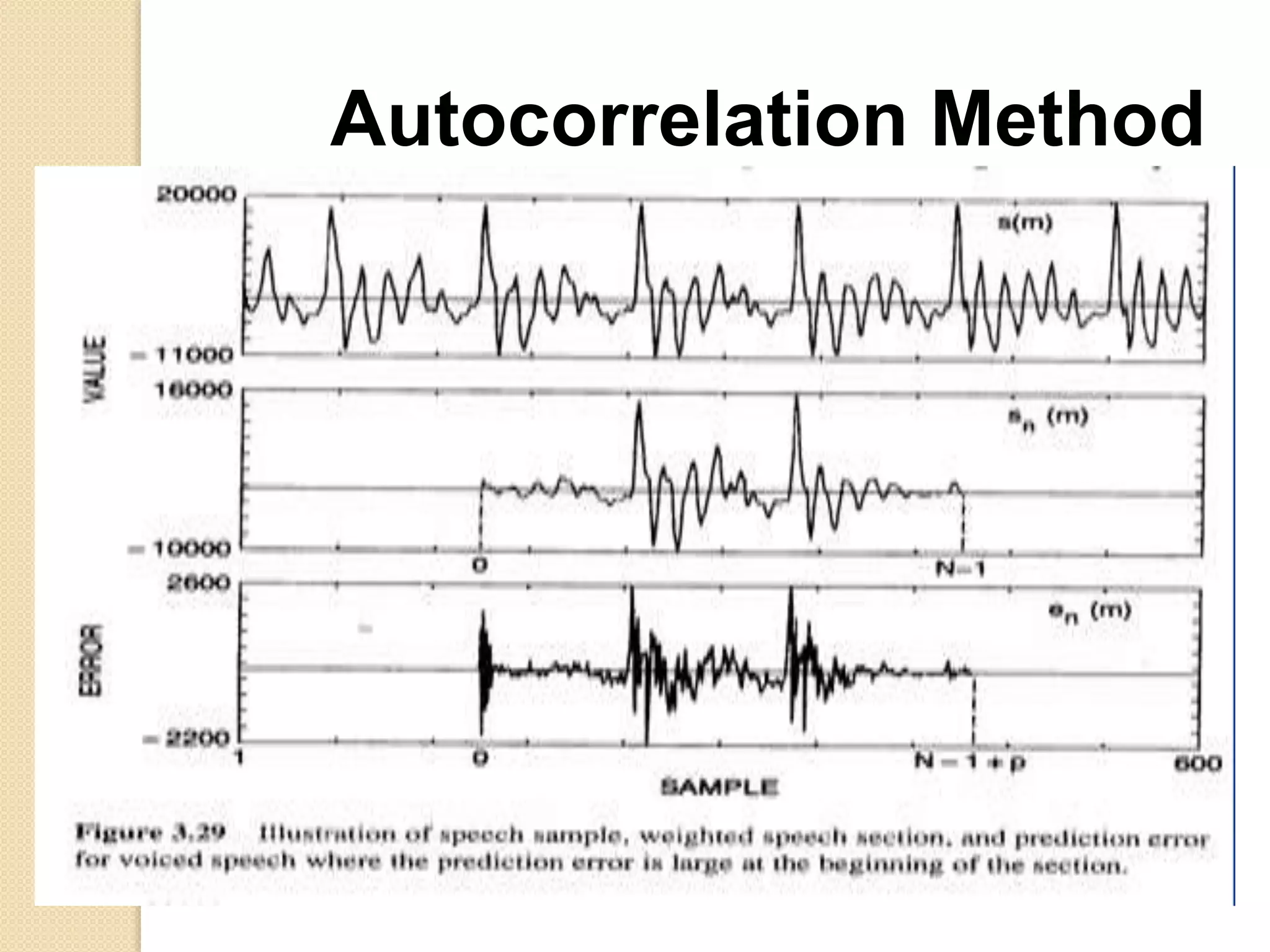
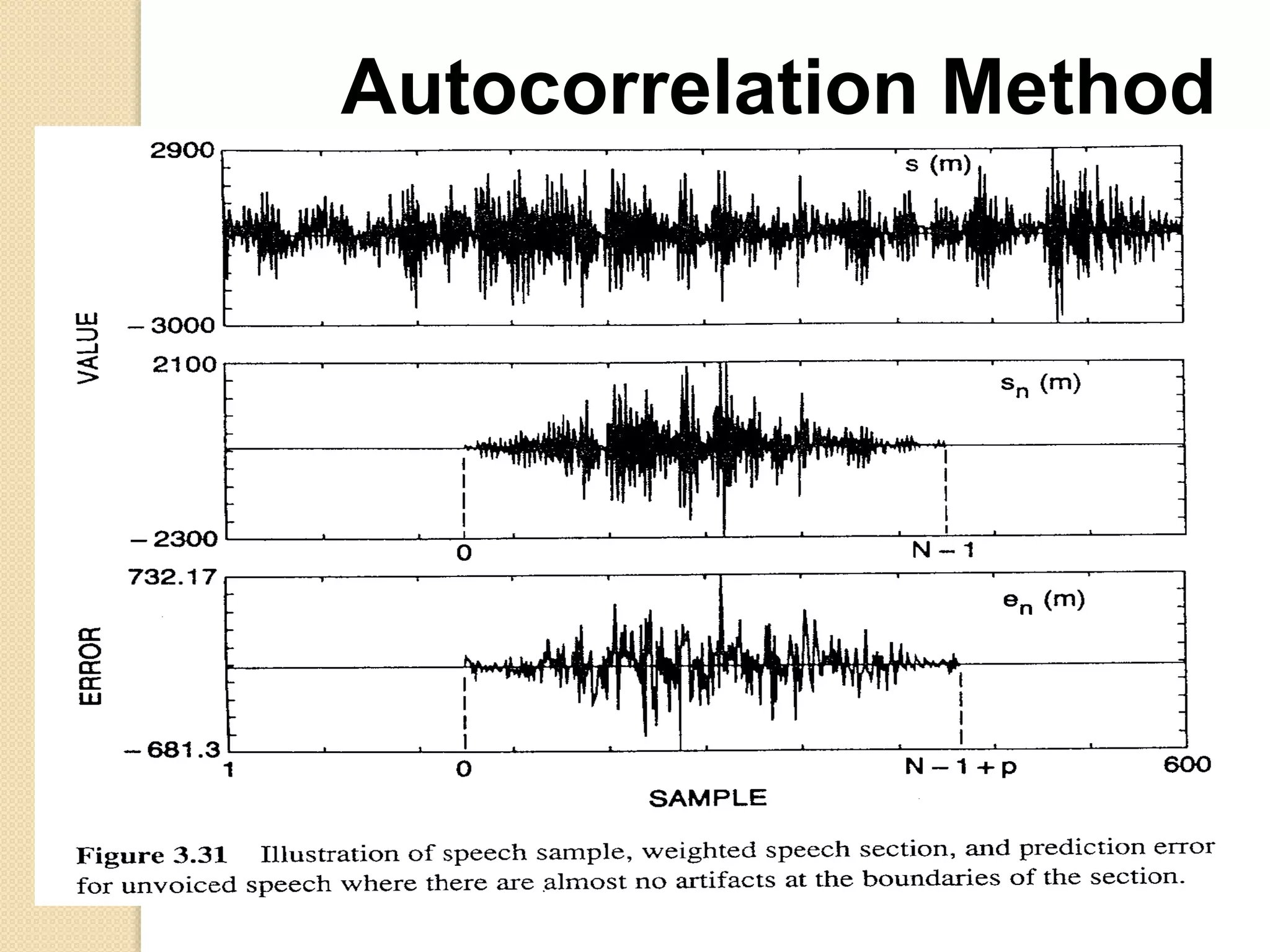
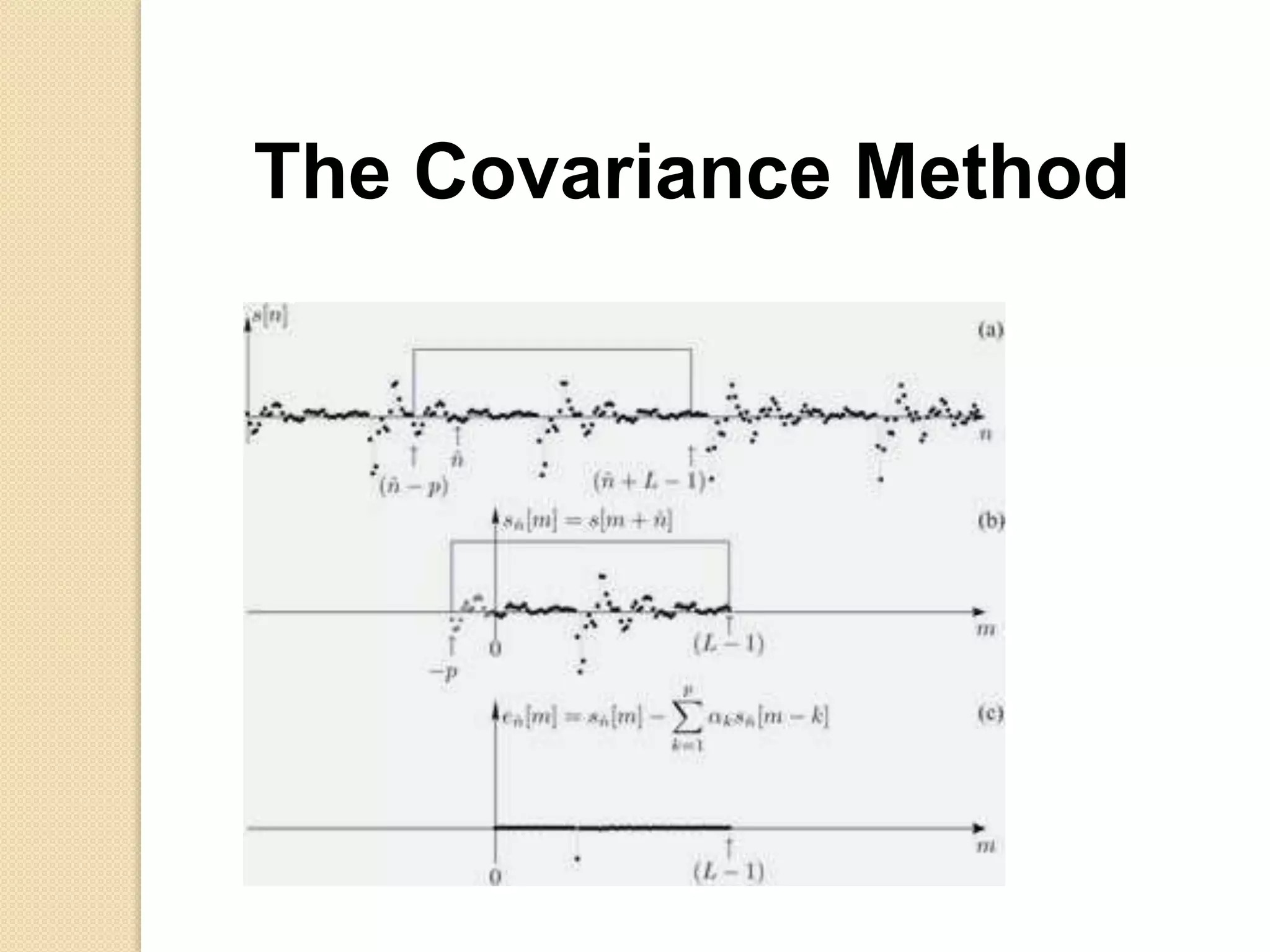
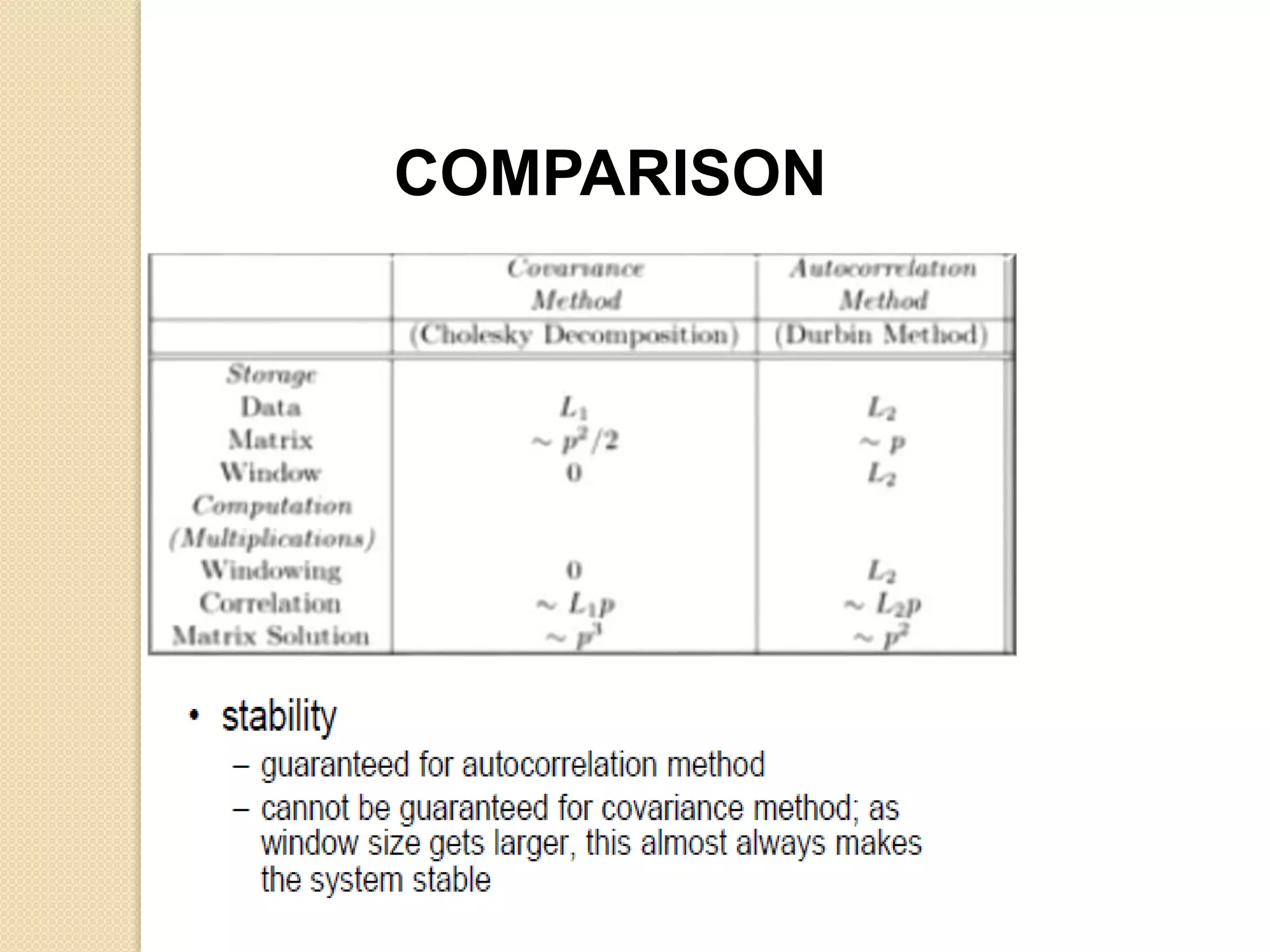
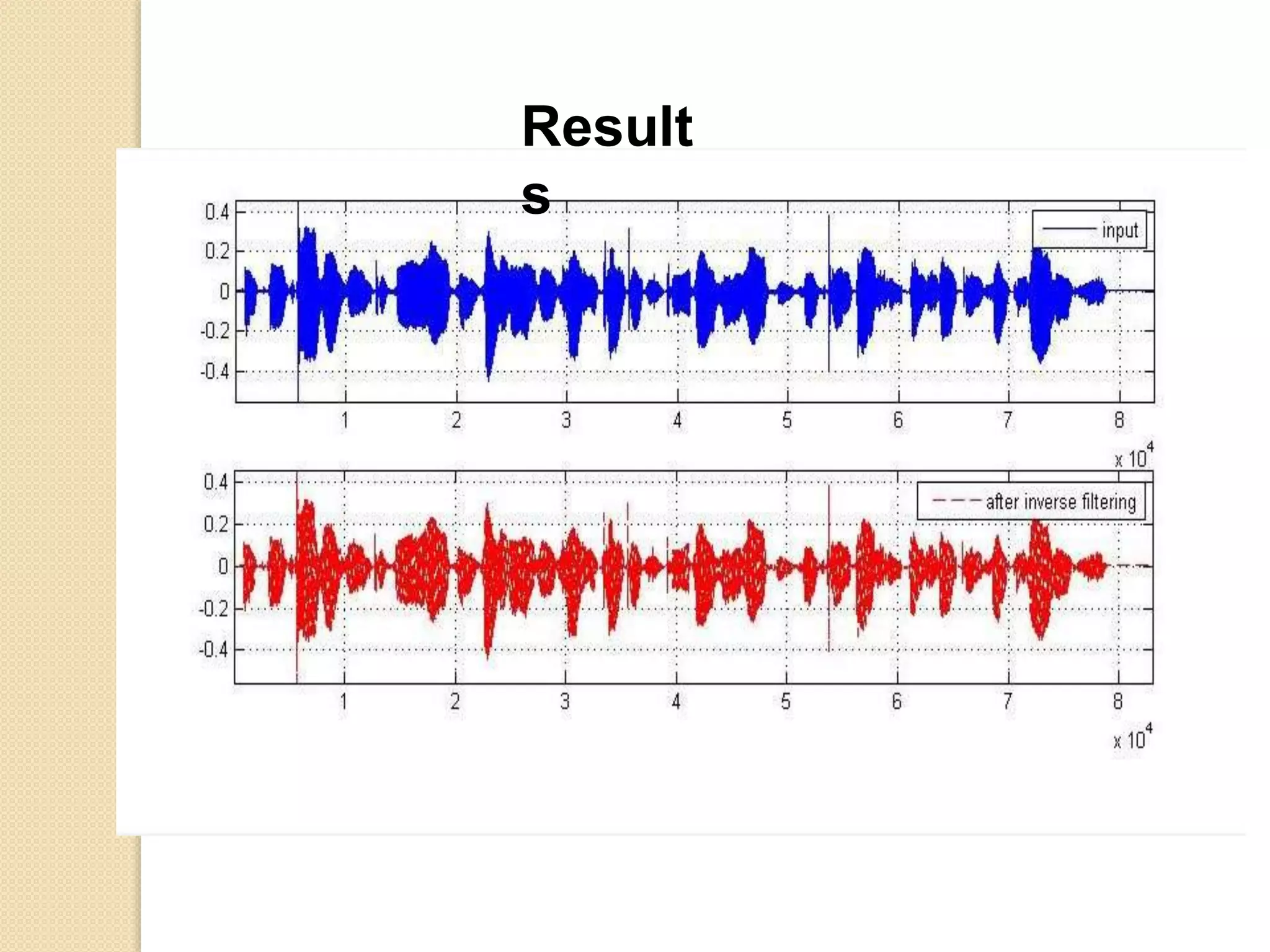
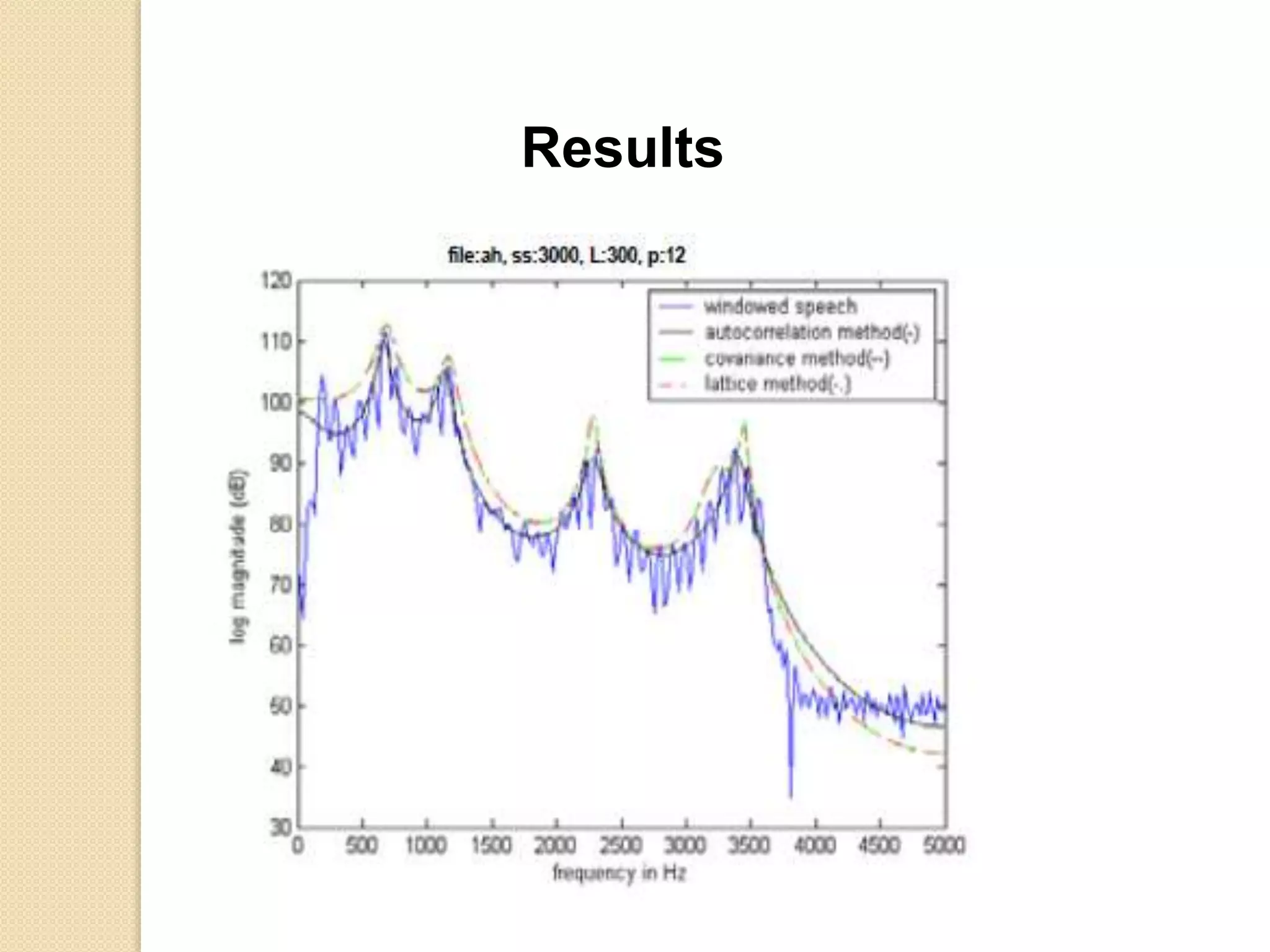
This document discusses linear predictive coding (LPC) methods and horn noise detection. It begins with an introduction to speech coders and speech production modeling. It then covers the basic principles of LPC analysis, including the autocorrelation and covariance methods. It discusses solving the LPC equations and using LPC residue to detect horn noise by comparing the residue of speech, silence and known horn noise samples. The document provides results of adding speech and horn noise signals and detecting the horn noise. It concludes by listing references on speech coding algorithms, LPC, and speech processing.