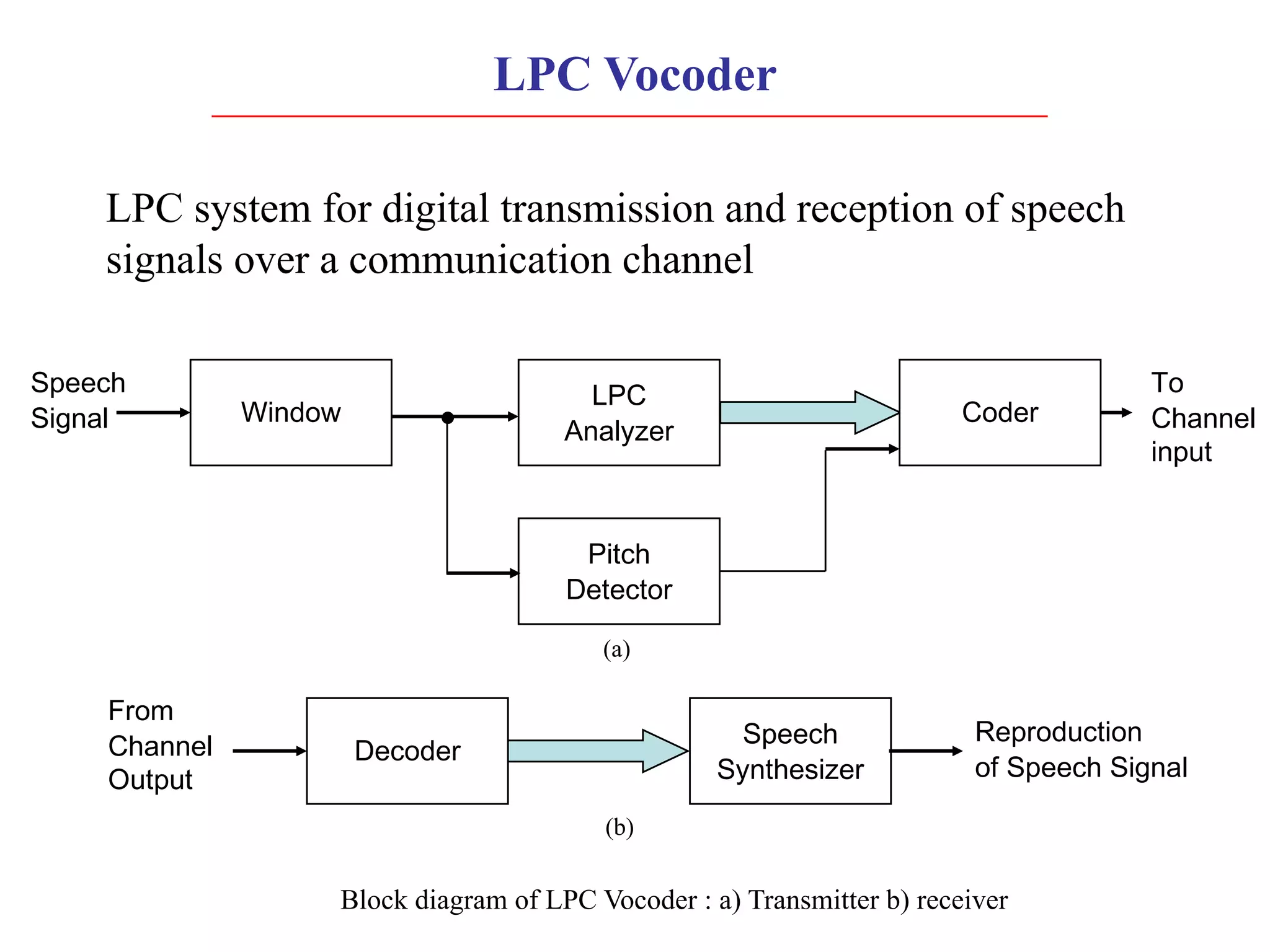
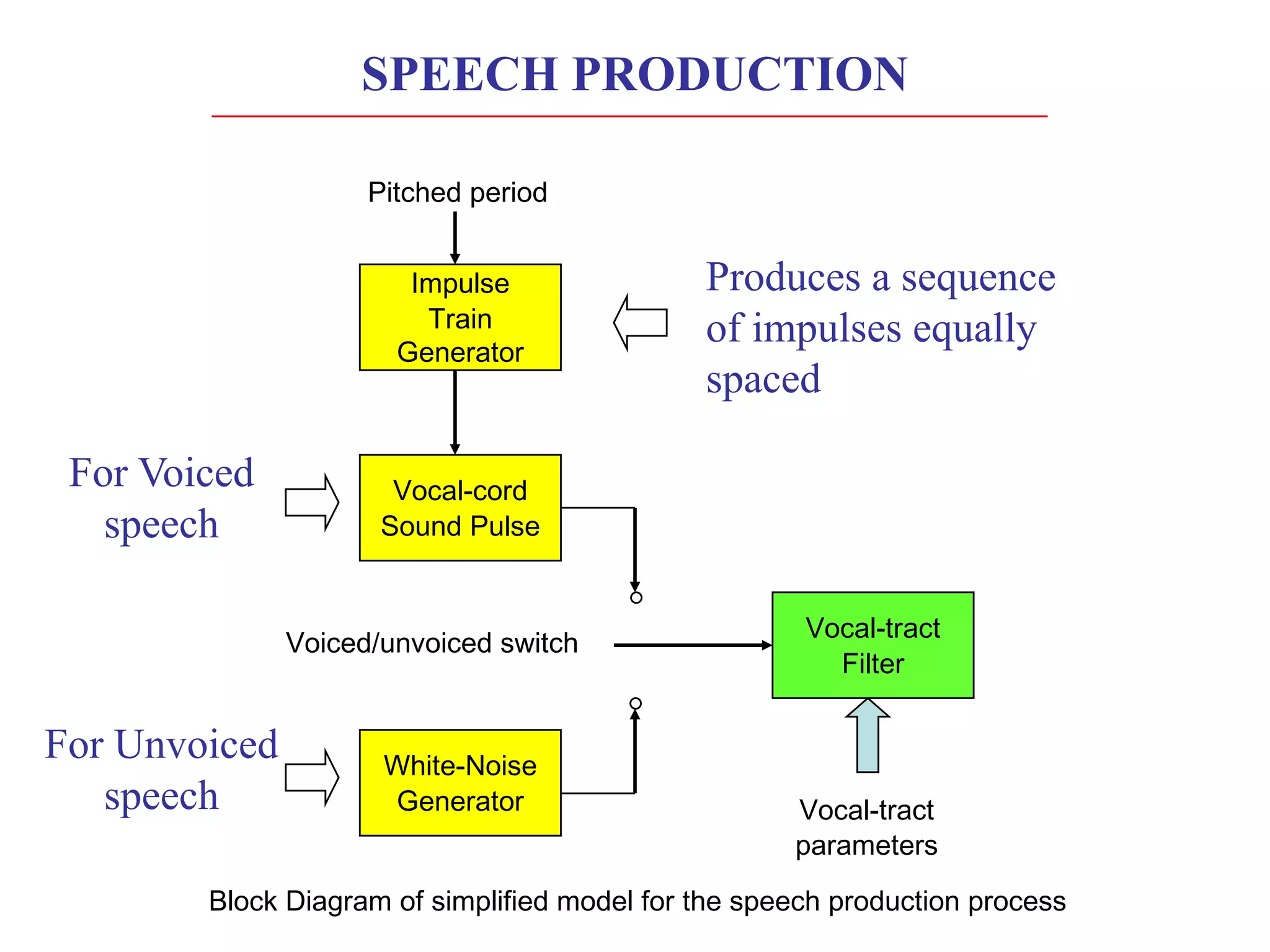
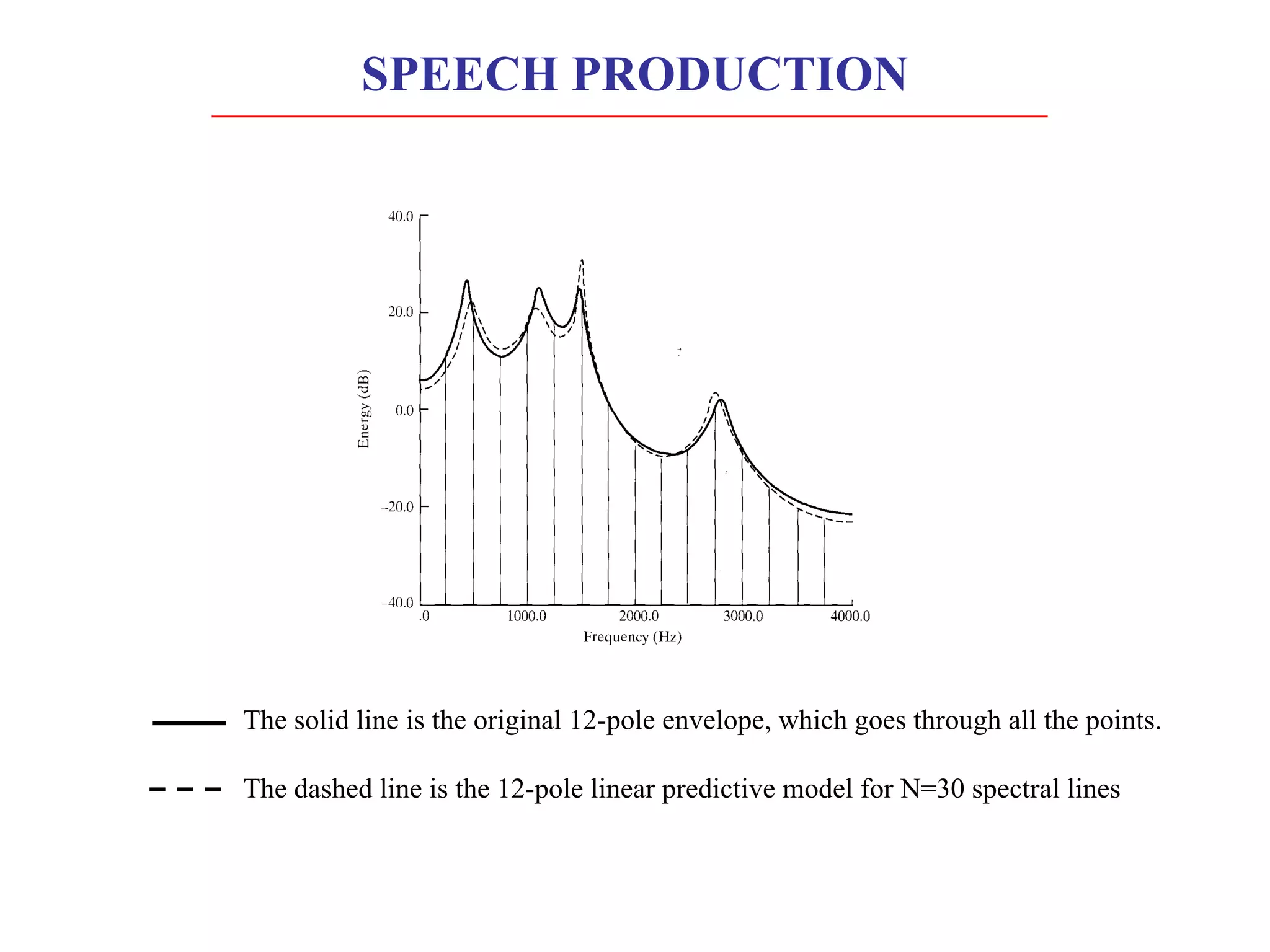
Linear predictive coding (LPC) models human speech production as a vocal tract represented by a tube of varying diameter. LPC is a digital encoding method that predicts signal values using a linear function of past values. The speech production process can be modeled as excitation of the vocal tract filter by either a periodic source for voiced sounds or random noise for unvoiced sounds. Accurately modeling the short-term power spectral envelope plays an important role in speech quality and intelligibility. The Itakura-Saito distance measure is an error criterion used in LPC that better models periodic signals like voiced speech. An LPC vocoder separates speech into parameters at the transmitter and re synthesizes speech from the parameters at the receiver.

1. Predictive Modeling of Speech
Dr. Yogananda Isukapalli

2. PREDICTIVE MODELING OF SPEECH
Linear Predictive Coding (LPC):
is defined as a digital method for encoding an analog signal in
which a particular value is predicted by a linear function of
the past values of the signal
- First proposed method for encoding Human Speech US DoD
- Human speech is produced in the vocal tract which can be
approximated as a variable diameter tube.
- The linear predictive coding (LPC) model is based on a
mathematical approximation of the vocal tract represented
by a tube of a varying diameter

3. Impulse
Train
Generator
Vocal-cord
Sound Pulse
White-Noise
Generator
Vocal-tract
Filter
Vocal-tract
parameters
Pitched period
Voiced/unvoiced switch
Block Diagram of simplified model for the speech production process
For Voiced
speech
For Unvoiced
speech
Produces a sequence
of impulses equally
spaced
SPEECH PRODUCTION

4. Ø The model assumes that the sound-generating mechanism
is linearly separable from the intelligence-modulating
vocal-tract filter.
Ø The precise form of the excitation depends on whether the
Speech is voiced or unvoiced.
• Voiced speech sound (such as /i/ in eve) is generated
from a quasi-periodic excitation of vocal-tract.
• Unvoiced speech sound (such as /f/ in fish) is generated
from random sounds produced by turbulent airflow
through a constriction along the vocal tract.
SPEECH PRODUCTION

5. SPEECH PRODUCTION
Vocal-tract filter is represented by the all-pole transfer function,
å
=
-
+
= M
k
k
k z
a
G
z
H
1
1
)
(
where
G: Gain factor
ak: Real-value coefficient
The form of excitation applied to this filter is changed by
switching between the voiced and unvoiced sounds.

6. SPEECH PRODUCTION
ü Accurate modeling the short-term power spectral
envelope plays an important role in the quality and
intelligibility of the reconstructed speech.
ü At low bit-rate speech coding, an all-pole filter is
adopted to model the spectral information in LPC
(linear predictive coding)-based coders.
ü By minimizing the MSE between the actual speech
samples and the predicted ones, an optimal set of
weights for an all-pole (synthesis) digital filter can
be determined

7. Assuming an “all-pole” model, irrespective of speech signal
envelope we are trying to estimate:
• If sound is unvoiced, usual LPC method gives “good
estimate” of filter coefficients ak
• If sound is voiced, usual LPC method gives a “biased
estimate” of ak with the estimate worsening as the
pitch increases (error criterion being MSE)
Example: This example illustrates the limitations of standard
all-pole modeling of periodic waveforms. Specifications are:
• All-pole filter order, M = 12
• Input Signal: periodic pulse sequence with N=32
SPEECH PRODUCTION

8. The solid line is the original 12-pole envelope, which goes through all the points.
The dashed line is the 12-pole linear predictive model for N=30 spectral lines
SPEECH PRODUCTION

9. Itakura-Saito distance measure:
Let u(n) be a real-valued, stationary stochastic process, it’s
Fourier Transform Uk is:
( ) 1
-
N
...
0,1,2,
k
1
0
=
= å
-
=
-
N
k
jn
n
k
k
e
u
U w
El-jaroudi and Makhoul used “Itakura-Saito distance measure”
as “error criterion” to overcome this problem to develop a
new model called “discrete all-pole model”.
SPEECH PRODUCTION

10. Let vector a denote a set of spectral parameters as:
T
M
a
a
a ]
,.....,
,
[
a 2
1
=
Note: See p.no.189-191 in textbook for proof
The auto-correlation function of u(n) for lag m is:
( )
( ) 1
-
N
...
0,1,2,
k
)
(
where
1
-
N
...
0,1,2,
k
1
)
(
1
0
1
0
=
=
=
=
å
å
-
=
-
-
=
N
k
jn
k
N
k
jn
k
k
k
e
m
r
S
e
S
N
m
r
w
w
SPEECH PRODUCTION

11. The time-reversed impulse response h(-i) of the discrete
frequency-sampled all-pole filter can be obtained from the
relation of predictor coefficients to the auto-correlation as:
å
=
-
=
-
M
k
k k
i
r
a
i
h
0
)
(
)
(
ˆ
å
-
=
÷
÷
ø
ö
ç
ç
è
æ
-
÷
÷
ø
ö
ç
ç
è
æ
-
=
1
0
2
2
1
)
(
ln
)
(
)
(
N
k k
k
k
k
IS
a
S
U
a
S
U
a
D
Itakura-Saito distance measure is given by:
SPEECH PRODUCTION

12. LPC Vocoder
LPC system for digital transmission and reception of speech
signals over a communication channel
Reproduction
of Speech Signal
From
Channel
Output
Speech
Signal
To
Channel
input
Window
LPC
Analyzer
Coder
Pitch
Detector
Block diagram of LPC Vocoder : a) Transmitter b) receiver
(b)
Decoder
Speech
Synthesizer
(a)

13. LPC Vocoder
Transmitter:
• Applies window (typically, 10 to 30 ms long) to the input
• Analyzes the input speech block by block
Ø Performs Linear prediction
Ø Pitch Detection
• Finally, following parameters are encoded:
Ø Set of coefficients computed by LPC Analyzer
Ø The Pitch Period
Ø The Gain parameter
Ø The voiced-unvoiced parameters

14. LPC Vocoder
Receiver:
Performs the inverse operations on the channel output:
• Decode incoming parameters
• Synthesize a speech signal from the parameters