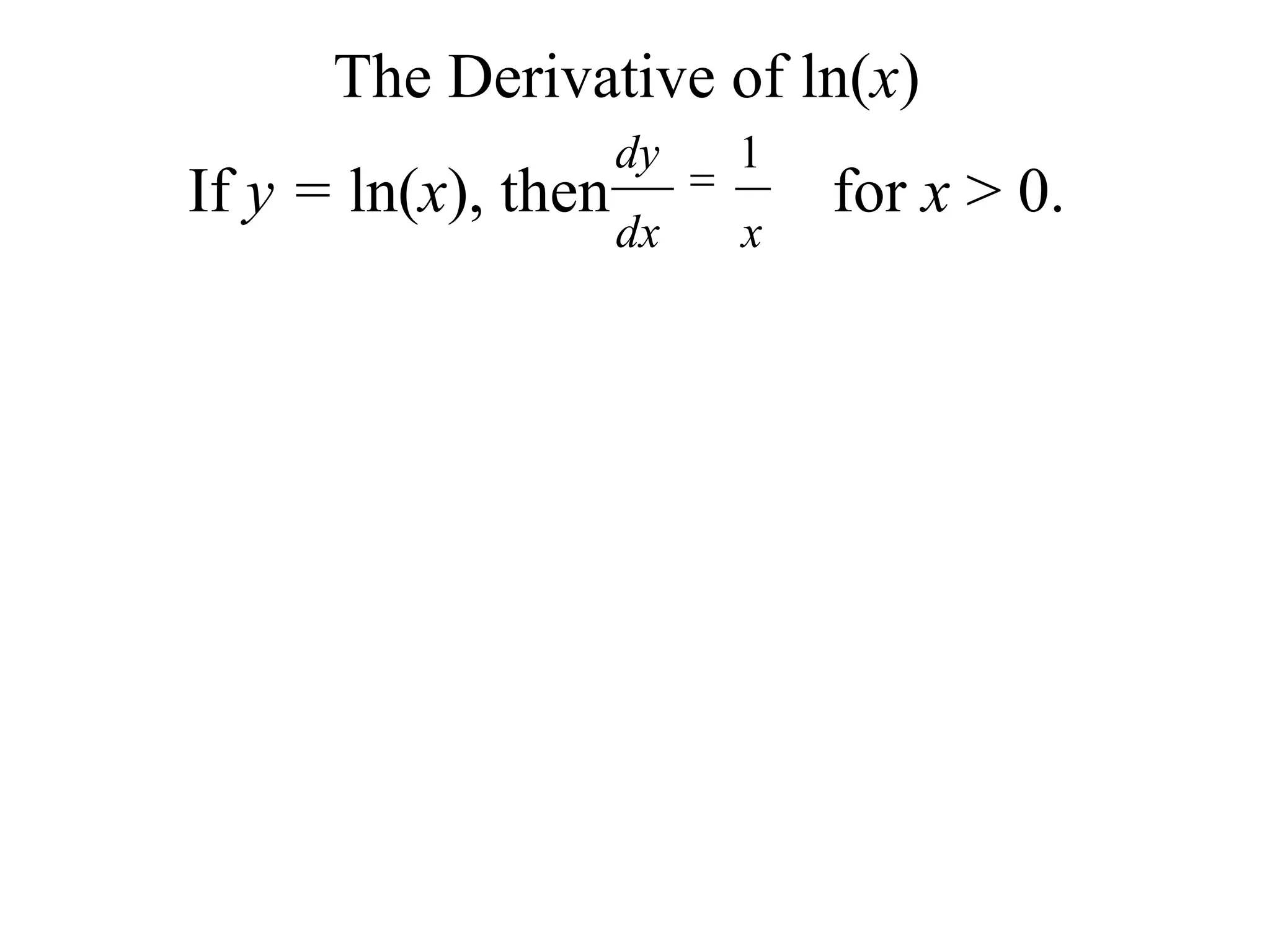The document discusses numerically estimating the derivative of ln(x) at different input values such as 10. It performs this estimation by taking the limit of the difference quotient as h approaches 0. The results show the derivative converges to 0.1. It then instructs to estimate derivatives for other functions and establishes the general rule that the derivative of ln(x) is the reciprocal, 1/x, for x > 0.

1. The Derivative of ln(x)Numerically estimate the derivative at the following input values.

2. Let’s see how this looks for x = 10.

3. Let’s see how this looks for x = 10.

4. Let’s see how this looks for x = 10.Now there’s not much simplification we can do here so let’s see what happens as h gets closer to 0

5. Let’s see how this looks for x = 10.Now there’s not much simplification we can do here so let’s see what happens as h gets closer to 0

6. Let’s see how this looks for x = 10.Now there’s not much simplification we can do here so let’s see what happens as h gets closer to 0

7. Let’s see how this looks for x = 10.Now there’s not much simplification we can do here so let’s see what happens as h gets closer to 0

8. Let’s see how this looks for x = 10.Now there’s not much simplification we can do here so let’s see what happens as h gets closer to 0So it converges to 0.1

9. The Derivative of ln(x)Numerically estimate the derivative at the following input values.

10. Now do the same thing to estimate the derivatives for the other functions.The Derivative of ln(x)Numerically estimate the derivative at the following input values.

11. The Derivative of ln(x)Numerically estimate the derivative at the following input values.

12. In each case the derivative is the reciprocal so we have our rule for f(x) = ln(x)The Derivative of ln(x)Numerically estimate the derivative at the following input values.

13. The Derivative of ln(x)If y = ln(x), then for x > 0.