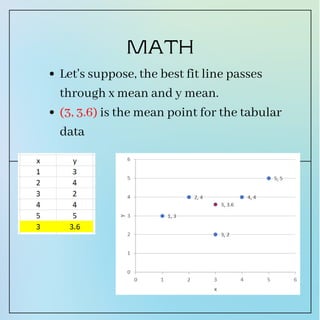
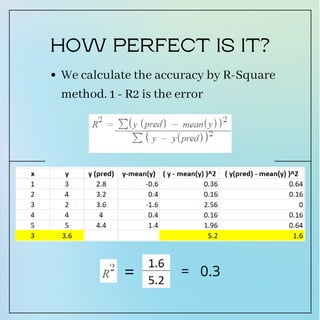
Linear regression is a simple supervised machine learning algorithm that finds the linear relationship between variables. It fits a linear equation to the data to predict the output value based on one or more predictor variables. The goal is to find the best fit line that minimizes the distance between the actual data points and the line. In Python, the scikit-learn library can be used to implement linear regression and evaluate the model accuracy using the R-squared metric.

1. LINEAR
REGRESSION
I N P Y T H O N

2. Type of Supervised Learning
Algorithm.
Regression refers to searching for
relationship between variables.
Simplest type of regression, used
Use Cases: predict sales, predict impact
of change of predictor, forecast, risk
assessment, check for trends
when variables are "linearly" related
WHAT IS IT?

3. Works on linear relationship of
variables
Example, lets have a small table:
Here, y is a dependent variable, which
depends on x.
MATH BEHIND

4. Find the best fit line, which goes or is
close to almost every point in the table
(data)
Let's suppose a line l passes through it.
l can be defined as:
It is the slope intercept form of line.
m is slope and c is the intercept for the
line which passes from (x,y)
y = m . x + c
GOAL

5. Let's suppose, the best fit line passes
through x mean and y mean.
(3, 3.6) is the mean point for the tabular
data
MATH

6. Slope, m of the line:
If the line passes through (3, 3.6) and
have slope m as 0.4, we can easily
determine 'c' by subsituting the values
and solving for 'c'.
3.6 = 0.4 (3) + c
Thus, c comes to be 2.4
MATH
2

7. The equation of lines comes to be:
This is our regression line.
Y (pred) are the predicted y values
corresponding to the x values
y = (0.4) x + 2.4
MATH

8. We calculate the accuracy by R-Square
method. 1 - R2 is the error
HOW PERFECT IS IT?
= = 0.3

9. Implementing the linear regression
using scikit learn.
SCIKIT LEARN