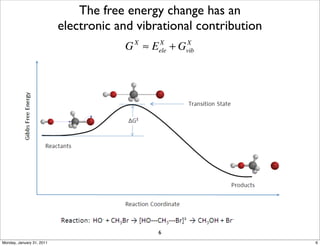
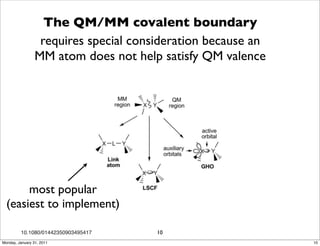
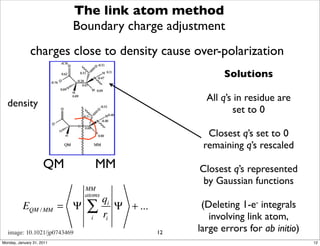
1) The document discusses the use of quantum mechanics/molecular mechanics (QM/MM) methods to study reaction mechanisms in enzymes. It outlines some of the challenges in applying these methods, including accurately computing energies and free energy contributions and finding transition states. 2) Key aspects of QM/MM calculations that are discussed include separating the electronic and vibrational contributions to free energy, treating the boundary between the QM and MM regions, and using molecular dynamics simulations to account for dynamic effects. 3) The document provides an overview of common approaches to addressing issues like computing energies, incorporating vibrational contributions, optimizing transition states, and representing the QM/MM boundary region in the calculations.

1. QM/MM methods applied to reaction
mechanisms in enzymes
Required for credit (7.5 ECTS):
Present the method used in
one of the papers on the list
Appreciated:
PDF file of slides before presentation (on web site)
Links to papers you used to prepare slides
Blog post* summarizing in-class discussion
Required for extra credit (2.5 ECTS):
Proposal describing improvement to QM/MM
*http://proteinsandwavefunctions.blogspot.com/
Monday, January 31, 2011 1

2. QM/MM methods applied to reaction
mechanisms in enzymes
Intro + 7 papers in 8 weeks
6 students: Casper, Anders, Martin, Kasper, Eric, Janus
Week 1 (Feb 3rd): Jan - QM/MM Background
Week 2 (Feb 10) Jan - Yang paper
Week 3 (Feb 17) ? - Paper ?
Week 4 (Feb 24) ? - Paper ?
Week 5 (March 10) ? - Paper ?
Week 6 (March 17) ? - Paper ?
Week 7 (March 24) ? - Paper ?
Week 8 (March 31) ? - Paper ?
2
Monday, January 31, 2011 2

3. Measured: rate [P]/s
Rate => kcat
10.1126/science.1088172 3
Monday, January 31, 2011 3

4. kcat is converted to free energy
via transition state theory
kcat ⇒ ΔG 0
act
Most QM/MM studies assume
ΔGextra ≈ 0
10.1126/science.1088172 4
Monday, January 31, 2011 4

5. The activation free energy
ΔG TS,0
=G −G TS ES
⎛ conformations
⎞
G = −RT ln ⎜
X
⎝
∑ e −GiX / RT
⎟
⎠
i
⎛ conformations
( ) ⎞
∑
− GiX −G0 / RT
X
= G − RT ln ⎜
X
e ⎟
⎝
0
i ⎠
0 is the conformation with lowest G
Some QM/MM studies assume
G ≈G X X
0
(this also assumes the lowest energy conf has been found)
5
Monday, January 31, 2011 5

6. The free energy change has an
electronic and vibrational contribution
G ≈ E +G
X X
ele
X
vib
6
Monday, January 31, 2011 6

7. Challenges for QM/MM studies
Computing Eele and Gvib
Finding the TS
Eele ≈ EQM + EMM + EQM / MM + Eboundary
7
image: 10.1080/01442350903495417
Monday, January 31, 2011 7

8. Computing the “electronic” QM/MM energy
Eele ≈ EQM + EMM + EQM / MM + Eboundary
EQM = Ψ H Ψ + ∑ ∑ Z I Z J RIJ
ˆ −1
I J >I
some
bonds angles dihedrals
∑ k (r − r ) ∑ k (θ − θ i,e ) + ∑ Vi ⎣1 ± cos ( niφi ) ⎦
2 2
EMM = i i i,e + i i ⎡ ⎤
i i i
MM MM
atoms atoms
⎛ Ai A j Bi B j qi q j ⎞
+∑ ∑ ⎝ − r 6 + r12 + r ⎟
⎜
i j >i ij ij ij ⎠
8
Monday, January 31, 2011 8

9. Computing the “electronic” QM/MM energy
MM QM MM QM MM
atoms
qi atoms atoms
ZI qj ⎛ AI A j BI B j ⎞
atoms atoms
EQM / MM = Ψ ∑ ri
Ψ + ∑∑ rIj
+ ∑ ∑ ⎝ − r 6 + r12 ⎠
⎜ ⎟
i I j I j Ij Ij
AI and BI may need to be re-adjusted
What are AI and BI for atoms in a TS?
Notice that Ψ is polarized by qi’s
(this is called electrostatic embedding)
9
Monday, January 31, 2011 9

10. The QM/MM covalent boundary
requires special consideration because an
MM atom does not help satisfy QM valence
most popular
(easiest to implement)
10.1080/01442350903495417 10
Monday, January 31, 2011 10

11. The link atom method
Boundary constraints
H
some
angles dihedrals
Eboundary = ki ( ri − ri,e ) + ∑ k (θ − θ i,e ) + ∑ Vi ⎣1 ± cos ( niφi ) ⎦
2 2
i i ⎡ ⎤
i i
image and text:10.1021/jp9924124
11
Monday, January 31, 2011 11

12. The link atom method
Boundary charge adjustment
charges close to density cause over-polarization
Solutions
All q’s in residue are
density
set to 0
Closest q’s set to 0
remaining q’s rescaled
QM MM Closest q’s represented
by Gaussian functions
MM
atoms
qi
EQM / MM = Ψ ∑ ri
Ψ + ... (Deleting 1-e- integrals
i involving link atom,
image: 10.1021/jp0743469 12 large errors for ab initio)
Monday, January 31, 2011 12

13. The Localized-SCF method
The density localized molecular orbital
of the boundary bond is kept frozen during the SCF
some
angles dihedrals
Eboundary = ki ( ri − ri,e ) + ∑ ki (θ i − θ i,e ) + ∑ Vi ⎣1 ± cos ( niφi ) ⎦
2 2
⎡ ⎤
i i
image: 10.1021/jp000887l text: 10.1016/S0009-2614(00)00289-X
13
Monday, January 31, 2011 13

14. The Generalized Hybrid Orbital method
frozen
orbital
vs
10.1080/01442350903495417 14
Monday, January 31, 2011 14

15. QM/MM = QM program + MM program
MM QM MM
atoms atoms atoms
qi ZI qj
ˆ
Eele = Ψ H + ∑ ri
Ψ + ∑ ∑ Z I Z J RIJ +
−1
∑∑ rIj
i I J >I I j
QM MM MM MM
atoms atoms
⎛ AI A j BI B j ⎞ atoms atoms
⎛ Ai A j Bi B j qi q j ⎞
+∑ ∑ ⎝ − r 6 + r12 ⎠ +
⎜ ⎟ ∑ ∑ ⎝ − r 6 + r12 + r ⎟
⎜
I j Ij Ij i j >i ij ij ij ⎠
some
bonds angles dihedrals
+ ∑ ki ( ri − ri,e ) + ∑ k (θ − θ i,e ) + ∑ Vi ⎣1 ± cos ( niφi ) ⎦
2 2
i i ⎡ ⎤
i i i
boundary boundary boundary
bonds angles dihedrals
∑ k (r − r ) ∑ k (θ − θ i,e ) + ∑ Vi ⎣1 ± cos ( niφi ) ⎦
2 2
+ i i i,e + i i ⎡ ⎤
i i i
15
Monday, January 31, 2011 15

16. QM/MM = QM program + MM program
Eele = EQM + EQM/mm + Eqm,MM + EMM
GAMESS, GAUSSIAN, Turbomole, Molpro, ...
Chemshell, QoMMMa, COMQUM
AMBER, CHARMM, GROMACS, ....
(some MM programs have semiempirical QM in them)
The interface programs also often perform
geometry optimizations after collecting
gradient terms from both programs
Monday, January 31, 2011 16

17. QM/MM = QM program + MM program
MM QM MM
atoms atoms atoms
qi ZI qj
EQM + EQM / mm ˆ
= ΨH+ ∑ ri
Ψ + ∑ ∑ Z I Z J RIJ +
−1
∑∑ rIj
i I J >I I j
QM MM boundary boundary boundary
⎛ AI A j BI B j ⎞
atoms atoms bonds angles dihedrals
∑ ∑ ⎝ − r 6 + r12 ⎠ + ∑ k (r − r ) ∑ k (θ − θ i,e ) + ∑ Vi ⎣1 ± cos ( niφi ) ⎦
2 2
Eqm / MM = ⎜ ⎟ i i i,e + i i ⎡ ⎤
I j Ij Ij i i i
some MM MM
bonds angles dihedrals atoms atoms
⎛ Ai A j Bi B j qi q j ⎞
∑ k (r − r ) ∑ k (θ − θ i,e ) + ∑ Vi ⎣1 ± cos ( niφi ) ⎦ + ∑ ∑ ⎝ − r 6 + r12 + r ⎟
2 2
EMM = i i i,e + i i ⎡ ⎤ ⎜
i i i i j >i ij ij ij ⎠
gQM , mm + g qm, MM
gx,QM / mm =
(
∂ EQM + EQM / mm )
∂xQM
∂Eqm / MM
g MM gx,qm / MM =
∂xQM
∂EMM
gx, MM =
∂x MM
Monday, January 31, 2011 17

18. QM/MM = QM program + MM program
Workflow
protein structure form PDB
repair, add hydrogens, determine protonation state
build in substrate
MM minimize, MD?
Define QM region => boundary
coord + charges fed into QM program
Compute EQM/mm + g for QM atoms
coord + vdW param for substrate fed into MM program
special MM parameters for boundary?
Compute Eqm/MM + EMM + g for all atoms
Add g’s compute new coord
Monday, January 31, 2011 18

19. Computing the QM/MM Gvib
Eele ≈ EQM + EMM + EQM / MM + Eboundary
∂ 2 Eele
H ij =
∂xi ∂y j
too time
matrix diagonalization
consuming for k = L HL
t
scales as N3
larger systems
ki
νi =
2π
⎛ e− hν /2 kT ⎞
Gvib = −RT ln ⎜ − hν /2 kT ⎟
⎝1− e ⎠
19
Monday, January 31, 2011 19

20. Computing the QM/MM Gvib
Solutions
1. ΔGvib ≈ 0
1.5ν kcal/mol

ZPE ≈ −1
1000 cm
i.e. breaking a covalent bond contributes
roughly 3-4 kcal/mol to ΔH vib
2. Compute Gvib for model reaction
(not good approximation of ΔSvib)
20
Monday, January 31, 2011 20

21. Finding the TS
Conventional TS finding algorithms
use the Hessian H
−1
q n +1 = q n − H g
n n
Common solution:
adiabatic mapping
21 text: 10.1080/01442350903495417
Monday, January 31, 2011 21

22. Dynamic Effects via MD
⎛ conformations
⎞
G = −RT ln ⎜
X
⎝
∑ e −GiX / RT
⎟
⎠
i
⎛ conformations
( ) ⎞
∑
− GiX −G0 / RT
X
= G − RT ln ⎜
X
e ⎟
⎝
0
i ⎠
⎡ 1 N − ( E (τ )− Eref ) / RT ⎤
≈G X
ref − RT ⎢ ∑ e ⎥
⎣ N τ =1 ⎦
E(t)’s are energies along an MD trajectory
Monday, January 31, 2011 22