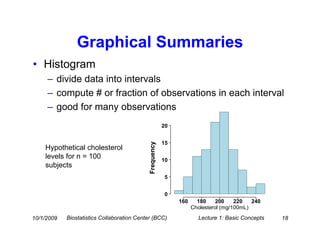
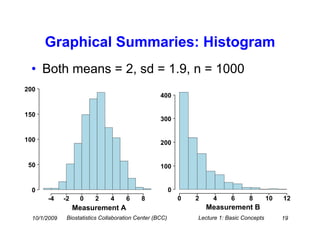
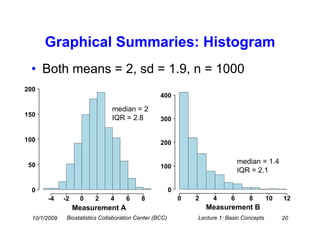
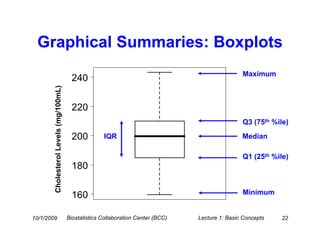
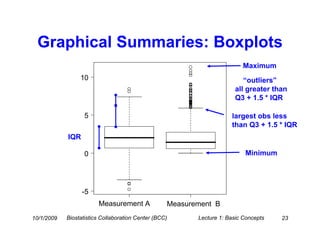
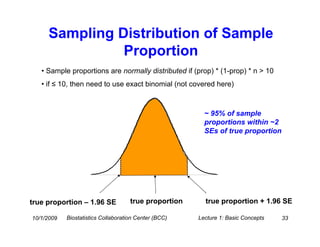
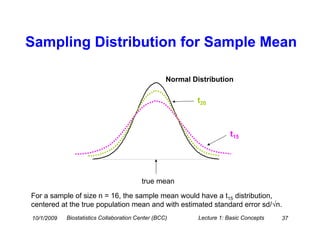
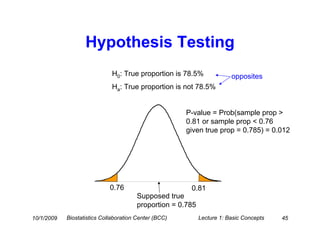
This document provides an overview of basic statistical concepts for medical research. It discusses different types of data including categorical and numerical data, and how to describe both types of data through summary statistics and graphical displays. Specific topics covered include determining data types, summarizing categorical variables with tables and percentages, summarizing numerical variables with measures of center like mean and median and measures of spread like standard deviation and interquartile range, and using histograms and boxplots for graphical summaries. The goal is to assist researchers in interpreting statistics and communicating with biostatisticians.