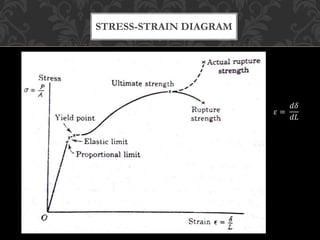
This document discusses simple strain and definitions related to stress-strain diagrams. It introduces key terms like elastic limit, yield point, ultimate stress, Hooke's law, modulus of elasticity, and shear deformation. Formulas are provided for axial deformation under Hooke's law, relating stress to strain. An example calculates the total deformation of an aluminum bar under an axial load based on its cross-sectional area and modulus of elasticity. A second example determines the vertical movement of a rigid bar attached to vertical rods under an applied load.

1. LEC03
SIMPLE STRAIN

2. Is there a change of the bar length?
What is deformation?
What is stiffness?
INTRODUCTION
BAR
P P

3. STRESS-STRAIN DIAGRAM
𝜀 =
𝑑𝛿
𝑑𝐿

4. DEFINITIONS
Proportional Limit
• Stress-strain diagram to be straight line.
• The stress is proportional to strain.
(Hooke’s Law)
Elastic Limit
• The stress beyond which the material will
not return to its original shape when
unloaded but will retain a permanent
deformation called the permanent set.

5. DEFINITIONS
Yield Point
• A point where there is an appreciable
elongation or yielding of the material without
any corresponding increase of load; indeed the
load may actually increase while the yielding
occurs.
Ultimate Stress/Ultimate Strength
• Highest ordinate in the SS curve.
Rupture Strength
• The stress at failure

6. HOOKE’S LAW: AXIAL
DEFORMATION
(From the SS curve)
The slope of the line is the ratio of stress to strain.
Young’s Modulus/Modulus of Elasticity = E =
𝜎
𝜀
𝜎 = 𝐸𝜀

7. HOOKE’S LAW: CONT…….
𝛿 =
𝑃𝐿
𝐴𝐸
=
𝜎𝐿
𝐸
(GENERAL FORMULA)
Restrictions:
• The load must be axial.
• The bar must have a constant cross section
and be homogeneous.
• The stress must not exceed the proportional
limit.

8. SHEARING
DEFORMATION
𝛿 =
𝑉𝐿
𝐴𝑠𝐺
Where;
G = modulus of elasticity in shear, more
commonly known as modulus of elasticity

9. AN ALUMINUM BAR HAVING A CROSS-SECTIONAL
AREA OF 160 MM^2 CARRIES AN AXIAL LOAD AT
THE POSITIONS SHOWN IN THE FIGURE. IF E = 70
GPA, COMPUTE THE TOTAL DEFORMATION OF
THE BAR. ASSUME THAT THE BAR IS SUITABLY
BRACED TO PREVENT BUCKLING.
ANS: 3.75 MM
EXAMPLE NO.02

10. The rigid bar AB, attached to two vertical rods as shown in
the figure, is horizontal before P is applied. If the load P =
50 kN, determine its vertical movement.
ANS; 1.814m
EXAMPLE NO.02