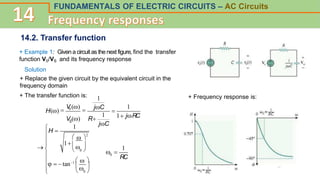
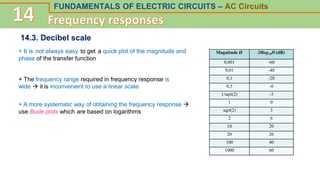
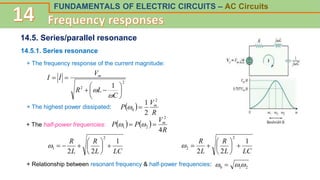
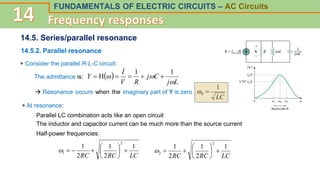
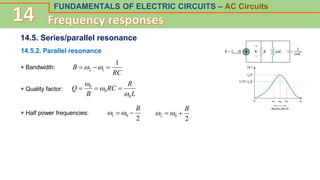
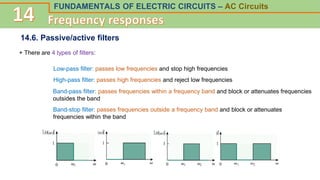
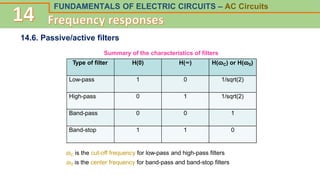
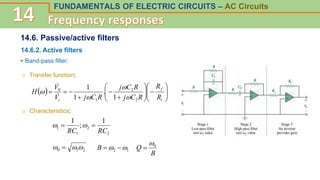
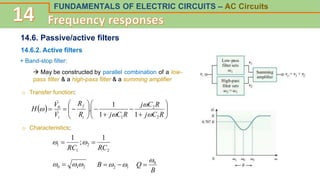
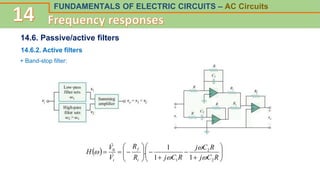
This document discusses frequency response and resonance in AC circuits. It begins by introducing the concept of a transfer function, which is the ratio of an output to an input of a circuit and describes its frequency response. Bode plots are then presented as a way to plot the magnitude and phase of a transfer function over frequency on logarithmic scales. The document covers series and parallel resonance, where the impedances of inductive and capacitive elements cancel out. Key concepts are introduced, such as resonant frequency, quality factor Q, and bandwidth, and how these relate to the selectivity of a resonant circuit.