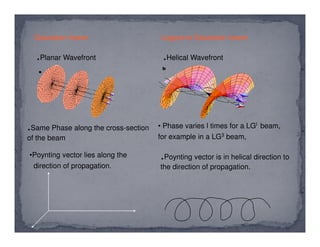
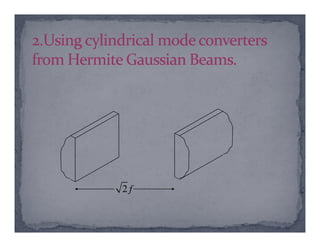
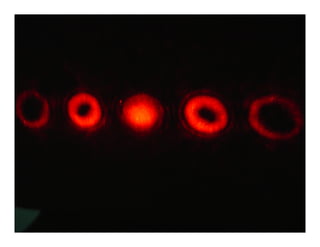
The document discusses the generation and applications of Laguerre-Gaussian beams in physics, highlighting their properties such as spin and orbital angular momentum. It also outlines various methods for generating these beams, including spiral phase plates and computer-generated holograms. Furthermore, it mentions potential applications in quantum communication and cryptography, emphasizing the advantages of Laguerre-Gaussian beams in trapping particles with minimal heating.

1. Presented by
Apurba Paul
PhD Student
Department of physics
Indian Institute of Science

2. Introduction
Gaussian beam
Laguerre-Gaussian beam
Generation
Application
Reference
Acknowledgement

3. 1.Plane waves.
2.Possess Linear momentum.
3.Remains Gaussian after reflection, refraction.3.Remains Gaussian after reflection, refraction.
4.Intensity profile is,
I (r) = I0 exp(−2r2 /w0
2 )

5. Are also called as,
– Optical Vortices,
– Helical beams,– Helical beams,
– Bottle beams,
– Twisted beams,
– Doughnut
beams….

6. Denoted by LGp
l
Have an azimuthal phase term exp(-ilφ)
Possesses,
-Spin Angular momentum due to ħ polarisation.-Spin Angular momentum due to ħ polarisation.
-Orbital Angular momentum of lħ due to the
optical phase profile of the beam.
Helical wavefronts
Have phase singularity.

7. 2
1
0 2 2
0 0
2 1
( , ) exp exp( )LG i
ρ
ρ φ ρ φ
ω ωπ
 
= − 
 
• Field amplitude is given by,
• Intensity Profile,• Intensity Profile,

8. Gaussian beam Laguerre Gaussian beam
.Planar Wavefront .Helical Wavefront
. • Phase varies l times for a LGl beam,.Same Phase along the cross-section
of the beam
• Phase varies l times for a LGl beam,
for example in a LG3 beam,
•Poynting vector lies along the
direction of propagation.
.Poynting vector is in helical direction to
the direction of propagation.

9. There are sevarel method of generation of Lagurre
Gaussian beam
1. Using spiral phase plate.
2. Using cylindrical mode converters from Hermite
Gaussian Beams.Gaussian Beams.
3. Using Computer Generated Hologram.

10. 1.Using spiral phase plate.

11. 2 f

12. Simplest mathematical form of phase singularity is,
0( , , ) exp( )exp( )E r z E il ikzθ θ= −
• For a plane wave,• For a plane wave,
exp( )x zu ik x ik z= − −
• The interference pattern is,
)cos(21 2
0 θlxkEEI x −++=

13. LG1
LG2 LG3
Some of the generated patterns.
LG4 LG6
LG5

14. • Photographically reduce
the output pattern…
• The reduced fringe width
should be equal to half
wavelength…wavelength…

17. 1.Reflective and absorptive particles can be trap in the dark
central spot, which by using Gaussian beam we can’t trap
2.The beam can transfer the angular momentum to
the trap particle and can make it rotate.
3. In case of cold atom trapping it spend maximum
time in the dark spot and causing less heating.
4. Life time of trapping is more than that in the
Gaussian beam

18. 1. Quantum Communication systems.
2. Quantum cryptography.

19. J. Arlt,K. Dholakia, L. Allen and M. J. Padget, Journal of Modern
Optics, 1998. vol 45, no 6, 1231-1237
H.He, N.R. Heckenber and H. Rubinsztein-Dunlop, Journal of
Modern Optics, 1995, vol 42, No. 1, 217-223
N. R. Heckenberg, R. McDuff, C. P. Smith, and A. G. White,
February 1 1992/vol 17, No. 3/ Optics LetterFebruary 1 1992/vol 17, No. 3/ Optics Letter
G. A. Turnbull, D. A, Robertson, G. M. Smith, L. Allen, M. J.
Padgent, Optics Communication 127 (1996) 183-188
Beijersbergen M. W, Allen L., Van Der Veen, H. E. L. O., and
Woerdman J. P., 1993, Optics Communication, 96, 123
Miles Padget and L. Allen, Contemporary Physics, 2000, volume
41, number 5, Pages 275-285
J. Courtial, M. J. Padgett, Optics Communication 159(1995) 13-18

20. I am very thank full to my guide Prof. Vasant Natarajan
and my lab mate, specially to Karthik for helping me
when ever I need it.
And thank to you all also for your kind attention and
cooperation.cooperation.