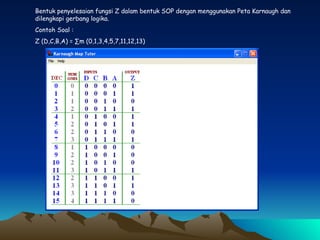
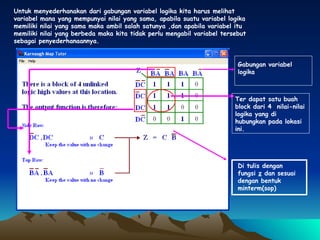
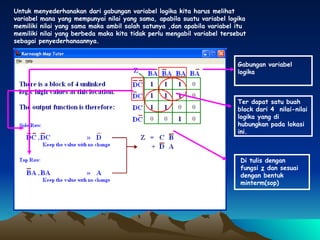
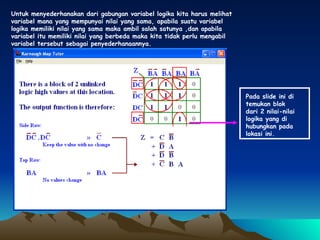
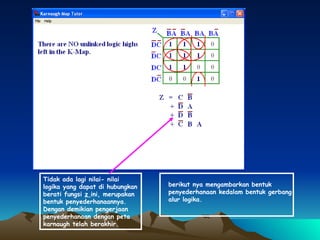
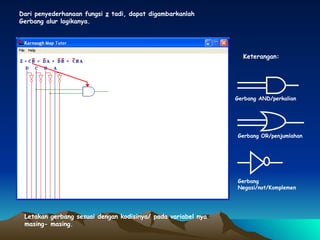
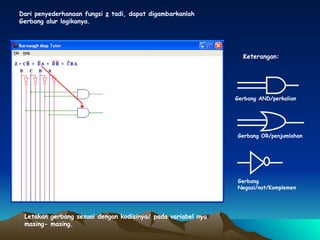
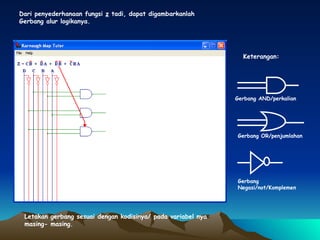
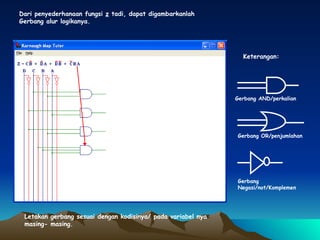
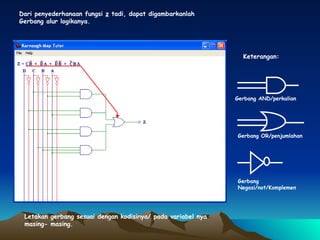
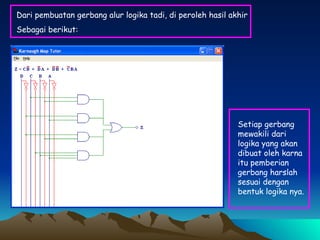
Dokumen ini membahas tentang penyederhanaan fungsi logika Z(D,C,B,A) menggunakan peta Karnaugh dan penggambaran hasilnya dalam bentuk gerbang logika. Fungsi logika tersebut disederhanakan menjadi blok-blok di peta Karnaugh lalu digambar menggunakan gerbang AND, OR, dan NOT.

1. TUGAS AKHIR LOGIKA INFORMATIKA DISUSUN OLEH: DICKY RYANTO MUKTI 0802041 AYU LESTARI 0802045 TRI AGUSWANTO 0802030

2. Bentuk penyelesaian fungsi Z dalam bentuk SOP dengan menggunakan Peta Karnaugh dan dilengkapi gerbang logika. Contoh Soal : Z (D,C,B,A) = ∑m (0,1,3,4,5,7,11,12,13)

3. Pada slide ini fungsi boolean tadi di masukan ke dalam peta karnaugh sesuai dengan alamat dari tabel. Alamat tempat pada peta karnaugh dapat dari Keterangan: D,C,BA = variabel fungsi (-) Diatas variabel = komplenamen variabel bernilai (0) Agar kita dapat menemukan minterm nya,kita harus tahu bahwa minterm mencari nilai yang = (1)

4. Sisi baris Puncak baris Untuk menyederhanakan dari gabungan variabel logika kita harus melihat variabel mana yang mempunyai nilai yang sama, apabila suatu variabel logika memiliki nilai yang sama maka ambil salah satunya ,dan apabila variabel itu memiliki nilai yang berbeda maka kita tidak perlu mengabil variabel tersebut sebagai penyederhanaannya. Gabungan variabel logika Ter dapat satu buah block dari 4 nilai-nilai logika yang di hubungkan pada lokasi ini. Di tulis dengan fungsi z dan sesuai dengan bentuk minterm(sop)

5. Sisi baris Puncak baris Untuk menyederhanakan dari gabungan variabel logika kita harus melihat variabel mana yang mempunyai nilai yang sama, apabila suatu variabel logika memiliki nilai yang sama maka ambil salah satunya ,dan apabila variabel itu memiliki nilai yang berbeda maka kita tidak perlu mengabil variabel tersebut sebagai penyederhanaannya. Gabungan variabel logika Ter dapat satu buah block dari 4 nilai-nilai logika yang di hubungkan pada lokasi ini. Di tulis dengan fungsi z dan sesuai dengan bentuk minterm(sop)

6. Sisi baris Puncak baris Untuk menyederhanakan dari gabungan variabel logika kita harus melihat variabel mana yang mempunyai nilai yang sama, apabila suatu variabel logika memiliki nilai yang sama maka ambil salah satunya ,dan apabila variabel itu memiliki nilai yang berbeda maka kita tidak perlu mengabil variabel tersebut sebagai penyederhanaannya. Gabungan variabel logika Ter dapat satu buah block dari 4 nilai-nilai logika yang di hubungkan pada lokasi ini. Di tulis dengan fungsi z dan sesuai dengan bentuk minterm(sop)

7. Pada slide ini di temukan blok dari 2 nilai-nilai logika yang di hubungkan pada lokasi ini. Untuk menyederhanakan dari gabungan variabel logika kita harus melihat variabel mana yang mempunyai nilai yang sama, apabila suatu variabel logika memiliki nilai yang sama maka ambil salah satunya ,dan apabila variabel itu memiliki nilai yang berbeda maka kita tidak perlu mengabil variabel tersebut sebagai penyederhanaannya.

8. Tidak ada lagi nilai- nilai logika yang dapat di hubungkan berati fungsi z ini, merupakan bentuk penyederhanaannya. Dengan demikian pengerjaan penyederhanaan dengan peta karnaugh telah berakhir. berikut nya mengambarkan bentuk penyederhanaan kedalam bentuk gerbang alur logika.

9. Dari penyederhanaan fungsi z tadi, dapat digambarkanlah Gerbang alur logikanya. Gerbang AND/perkalian Gerbang Negasi/not/Komplemen Gerbang OR/penjumlahan Letakan gerbang sesuai dengan kodisinya/ pada variabel nya masing- masing. Keterangan:

10. Dari penyederhanaan fungsi z tadi, dapat digambarkanlah Gerbang alur logikanya. Gerbang AND/perkalian Gerbang Negasi/not/Komplemen Gerbang OR/penjumlahan Letakan gerbang sesuai dengan kodisinya/ pada variabel nya masing- masing. Keterangan:

11. Dari penyederhanaan fungsi z tadi, dapat digambarkanlah Gerbang alur logikanya. Gerbang AND/perkalian Gerbang Negasi/not/Komplemen Gerbang OR/penjumlahan Letakan gerbang sesuai dengan kodisinya/ pada variabel nya masing- masing. Keterangan:

12. Dari penyederhanaan fungsi z tadi, dapat digambarkanlah Gerbang alur logikanya. Gerbang AND/perkalian Gerbang Negasi/not/Komplemen Gerbang OR/penjumlahan Letakan gerbang sesuai dengan kodisinya/ pada variabel nya masing- masing. Keterangan:

13. Dari penyederhanaan fungsi z tadi, dapat digambarkanlah Gerbang alur logikanya. Gerbang AND/perkalian Gerbang Negasi/not/Komplemen Gerbang OR/penjumlahan Letakan gerbang sesuai dengan kodisinya/ pada variabel nya masing- masing. Keterangan:

14. Dari pembuatan gerbang alur logika tadi, di peroleh hasil akhir Sebagai berikut: Setiap gerbang mewakili dari logika yang akan dibuat oleh karna itu pemberian gerbang harslah sesuai dengan bentuk logika nya.