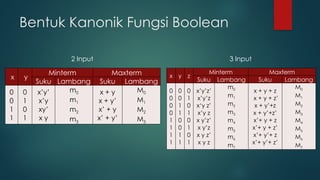
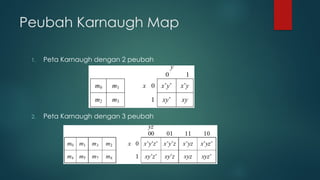
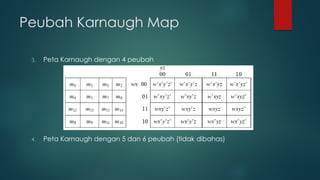
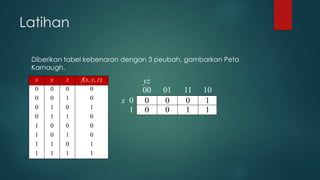
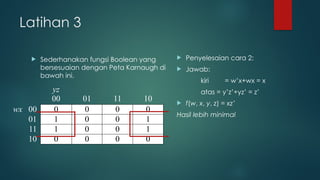
Dokumen ini membahas tentang penyederhanaan rangkaian logika menggunakan aljabar boolean dan peta Karnaugh (k-map) untuk fungsi logika. Materi mencakup teknik reduksi fungsi boolean, bentuk kanonik, serta latihan dalam menyederhanakan fungsi logika dengan 2, 3, dan 4 peubah. K-map digunakan untuk meningkatkan efisiensi rangkaian logika dengan meminimalkan jumlah gerbang yang diperlukan.

1. FT 1010 Sistem
Digital
DOSEN AJAR: MAHESA SANGGA BHUWANA S.T., M.T.

2. Outline
 Sekilas Aljabar Boolean pada Persamaan Logika
• Penyederhanaan Rangkaian Logika Secara Aljabar
• Bentuk Kanonik Fungsi Boolean
 Karnaugh Map pada Persamaan Logika
• Penjelasan Karnaugh Map
• Peubah Karnaugh Map
• Bentuk SOP atau POS
• Teknik Reduksi Fungsi Boolean dengan Karnaugh Map SOP
• Latihan-latihan

3. Sekilas Aljabar Boolean pada
Persamaan Logika

4. Penyederhanaan Rangkaian
Logika Secara Aljabar
 Tahap minimalisasi rangkaian logika agar efektif dan efisiensi
 Rangkaian dengan jumlah gerbang yang sedikit akan lebih murah
harganya, dan tata letak komponen lebih sederhana.
 Salah satu cara untuk meminimalkannya adalah dengan
menggunakan Aljabar Boolean.

5. Penyederhanaan Rangkaian
Logika Secara Aljabar
Contoh:
1.
Sehingga rangkaian diatas bisa disederhanakan menjadi:
A A B B
Y
Bentuk Aljabarnya adalah
Y = AB’ + A.B
Maka bisa disederhanakan menjadi
Y = A (B’ + B)
= A
A A B B
Y

6. Penyederhanaan Rangkaian
Logika Secara Aljabar
Contoh:
2.
Sehingga rangkaian diatas bisa
disederhanakan menjadi:
Bentuk Aljabarnya adalah
Y = A + ((A+B) . (B.C))
Maka bisa disederhanakan menjadi
Y = A + A B C + B B C ~B . B = B
= A + A B C + B C
= A + B C (A + 1) ~A+1=1
= A + B C
A
B
C
Y
A
B
C
Y

7. Bentuk Kanonik Fungsi Boolean
x y
Minterm Maxterm
Suku Lambang Suku Lambang
0
0
1
1
0
1
0
1
x’y’
x’y
xy’
x y
m0
m1
m2
m3
x + y
x + y’
x’ + y
x’ + y’
M0
M1
M2
M3
x y z
Minterm Maxterm
Suku Lambang Suku Lambang
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
x’y’z’
x’y’z
x‘y z’
x’y z
x y’z’
x y’z
x y z’
x y z
m0
m1
m2
m3
m4
m5
m6
m7
x + y + z
x + y + z’
x + y’+z
x + y’+z’
x’+ y + z
x’+ y + z’
x’+ y’+ z
x’+ y’+ z’
M0
M1
M2
M3
M4
M5
M6
M7
2 Input 3 Input

8. Karnaugh Map pada Persamaan
Logika

9. Penjelasan Karnaugh Map
 Karnaugh Map atau K-Map adalah adalah suatu teknik
penyederhanaan fungsi logika dengan cara pemetaan.
 K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah
variable dan fungsi logika atau jumlah inputan dari rangkaian
logika yang sedang kita hitung.
 Langkah – langkah pemetaan K-Map secara umum :
1. Pilih kotak karnaugh map dari jumlah peubah
2. Identifikasi minterm atau maxterm (mn atau Mn)
3. Tentukan cara SOP atau POS

10. Peubah Karnaugh Map
1. Peta Karnaugh dengan 2 peubah
2. Peta Karnaugh dengan 3 peubah

11. Peubah Karnaugh Map
3. Peta Karnaugh dengan 4 peubah
4. Peta Karnaugh dengan 5 dan 6 peubah (tidak dibahas)

12. Latihan
Diberikan tabel kebenaran dengan 3 peubah, gambarkan Peta
Karnaugh.
x y z f(x, y, z)
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
yz
00 01 11 10
x 0 0 0 0 1
1 0 0 1 1

13. Bentuk SOP atau POS
y’z’
00
y’z
01
yz
11
yz’
10
w’x’ 00 0 0 0 0
w’x 01 0 0 0 0
wx 11 0 0 1 1
wx’ 10 0 0 0 0
y’z’
00
y’z
01
yz
11
yz’
10
w’x’ 00 1 1 1 1
w’x 01 1 1 1 1
wx 11 1 1 0 0
wx’ 10 1 1 1 1
SOP
f(w, x, y, z) = wxyz + wxyz’
Lihat ke kiri = wx
Lihat ke atas = yz+yz’
= y
Jadi f(w,x,y,z) = wxy
POS
f(w, x, y, z) = (w+x+y+z) . (w+x+y+z’)
Lihat ke kiri = w+x
Lihat ke atas = (y+z). (y+z’)
= y + (z . z’)
= y + 0 = y
Jadi f(w,x,y,z) = (w+x) . y

14. Teknik Reduksi Fungsi Boolean
dengan Karnaugh Map SOP
1. Pasangan
2. Quad
3. Oktet

15. 1. Pasangan
 Dua buah nilai 1 yang bertetangga
 Bisa horizontal atau vertikal
yz
00 01 11 10
wx 00 0 0 0 0
01 0 0 0 0
11 0 0 1 1
10 0 0 0 0
 Sebelum disederhanakan: f(w, x, y, z)
= wxyz + wxyz’
 Hasil Penyederhanaan Kmap:
Lihat ke kiri = wx
Lihat ke atas = yz+yz’
= y
Jadi f(w,x,y,z) = wxy
 Bukti secara aljabar:
f(w, x, y, z) = wxyz + wxyz’
= wxy(z + z’)
= wxy(1)
= wxy

16. 2. Quad
 Empat buah nilai 1 yang bertetangga
 Bisa horizontal dan vertikal
 Juga dalam bentuk 2x2
yz
00 01 11 10
wx 00 0 0 0 0
01 0 0 0 0
11 1 1 1 1
10 0 0 0 0
 Sebelum disederhanakan: f(w, x, y, z) =
wxy’z’ + wxy’z + wxyz + wxyz’
 Hasil penyederhanaan:
Lihat kekiri = wx
Lihat keatas = y’z’+yz+y’z+yz’ (saling
menghilangkan)
= 1
f(w, x, y, z) = wx

17. 2. Quad
 Contoh lain:
yz
00 01 11 10
wx 00 0 0 0 0
01 0 0 0 0
11 1 1 0 0
10 1 1 0 0
 Sebelum disederhanakan: f(w, x, y, z) =
wxy’z’ + wxy’z + wx’y’z’ + wx’y’z
 Hasil penyederhanaan:
lihat kekiri = wx+wx’ (distributif)
= w
lihat keatas = y’z’+y’z
=y’
f(w, x, y, z) = wy’

18. 3. Oktet
 Delapan buah nilai 1 yang bertetangga
 Bisa horizontal dan vertikal
 Dalam bentuk 2x4
yz
00 01 11 10
wx 00 0 0 0 0
01 0 0 0 0
11 1 1 1 1
10 1 1 1 1
 Sebelum disederhanakan: f(w, x, y, z) =
wxy’z’ + wxy’z + wxyz + wxyz’ + wx’y’z’ +
wx’y’z + wx’yz + wx’yz’
 Hasil penyederhanaan:
dilihat kekiri = wx+wx’
= w
dilihat keatas = y’z’+yz+y’z+yz’
= 1
 f(w, x, y, z) = w

19. Latihan 1
 Andaikan suatu tabel kebenaran telah
diterjemahkan ke dalam Peta Karnaugh.
Sederhanakan fungsi Boolean yang
bersesuaian sesederhana mungkin.
yz
00 01 11 10
wx 00 0 1 1 1
01 0 0 0 1
11 1 1 0 1
10 1 1 0 1
 Jawab:
• Merah = wy’
kiri = wx+wx’ = w
atas = y’z’+y’z = y’
• Kuning = w’x’z
kiri = w’x’
atas = y’z+yz = z
• Hijau = yz’
kiri = w’x’+w’x+wx+wx’ = 1
atas = yz’
 f(w, x, y, z) = wy’+w’y’z+yz’

20. Latihan 2
 Minimisasi fungsi Boolean yang
bersesuaian dengan Peta Karnaugh di
bawah ini.
yz
00 01 11 10
wx 00 0 0 0 0
01 0 1 0 0
11 1 1 1 1
10 1 1 1 1
 Jawab:
• Merah = w
kiri = wx+wx’ = w
atas = y’z’+yz+y’z+yz’ = 1
• Kuning = xy’z
kiri = w’x+wx = x
atas = y’z
 f(w, x, y, z) = w + xy’z

21. Latihan 3
 Sederhanakan fungsi Boolean yang
bersesuaian dengan Peta Karnaugh di
bawah ini.
 Penyelesaian cara 1:
 Jawab:
• Merah = xy’z’
kiri = w’x+wx = x
atas = y’z’
• Kuning = xyz’
kiri = w’x+wx = x
atas = yz’
 f(w, x, y, z) = xy’z + xyz’
yz
00 01 11 10
wx 00 0 0 0 0
01 1 0 0 1
11 1 0 0 1
10 0 0 0 0

22. Latihan 3
 Sederhanakan fungsi Boolean yang
bersesuaian dengan Peta Karnaugh di
bawah ini.
 Penyelesaian cara 2:
 Jawab:
kiri = w’x+wx = x
atas = y’z’+yz’ = z’
 f(w, x, y, z) = xz’
Hasil lebih minimal
yz
00 01 11 10
wx 00 0 0 0 0
01 1 0 0 1
11 1 0 0 1
10 0 0 0 0

23. Materi minggu depan
 Lanjutan karnaugh map untuk yang bentuk POS
 Kondisi don’t care dalam karnaugh map

24. Terimakasih..