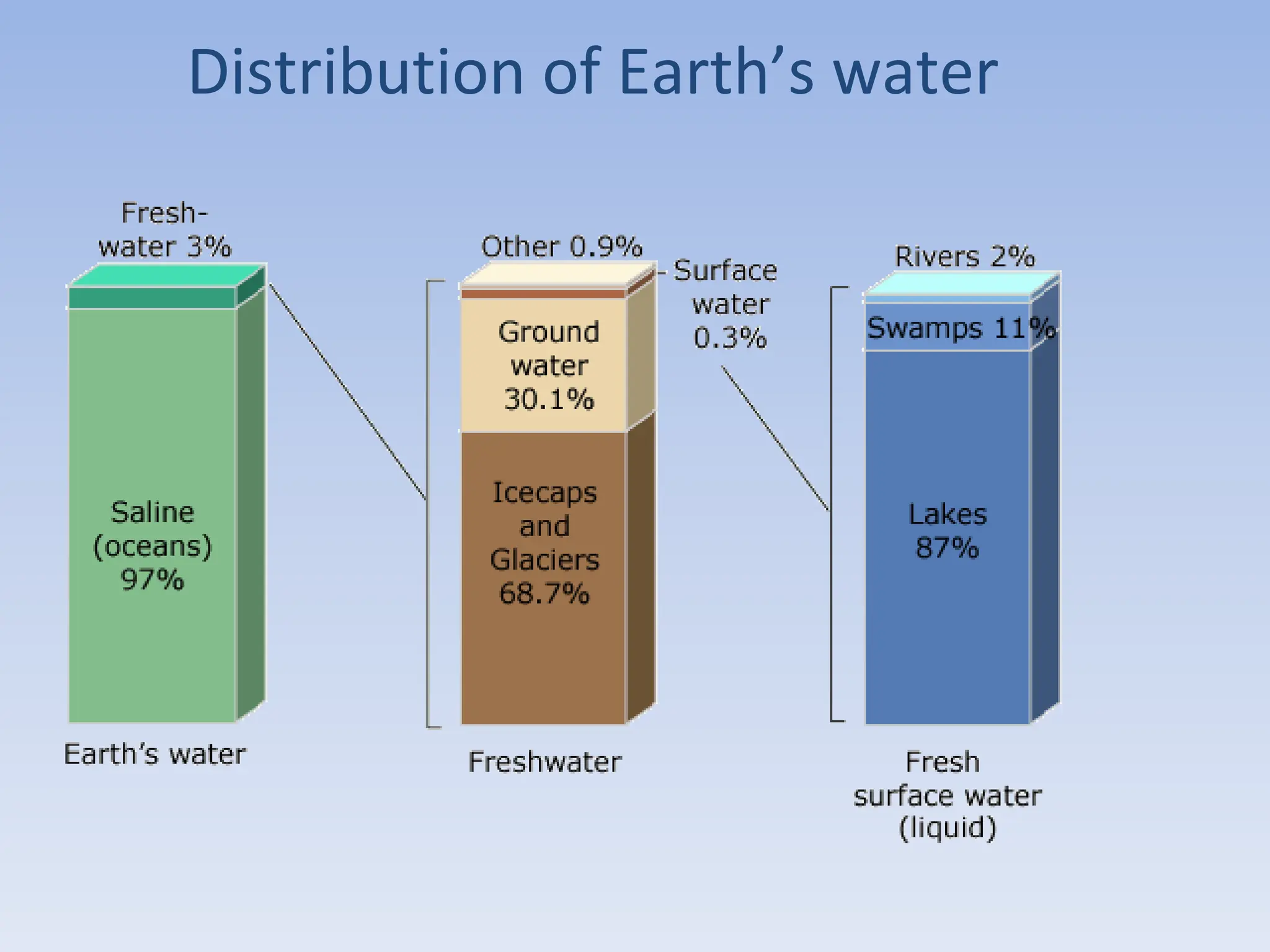
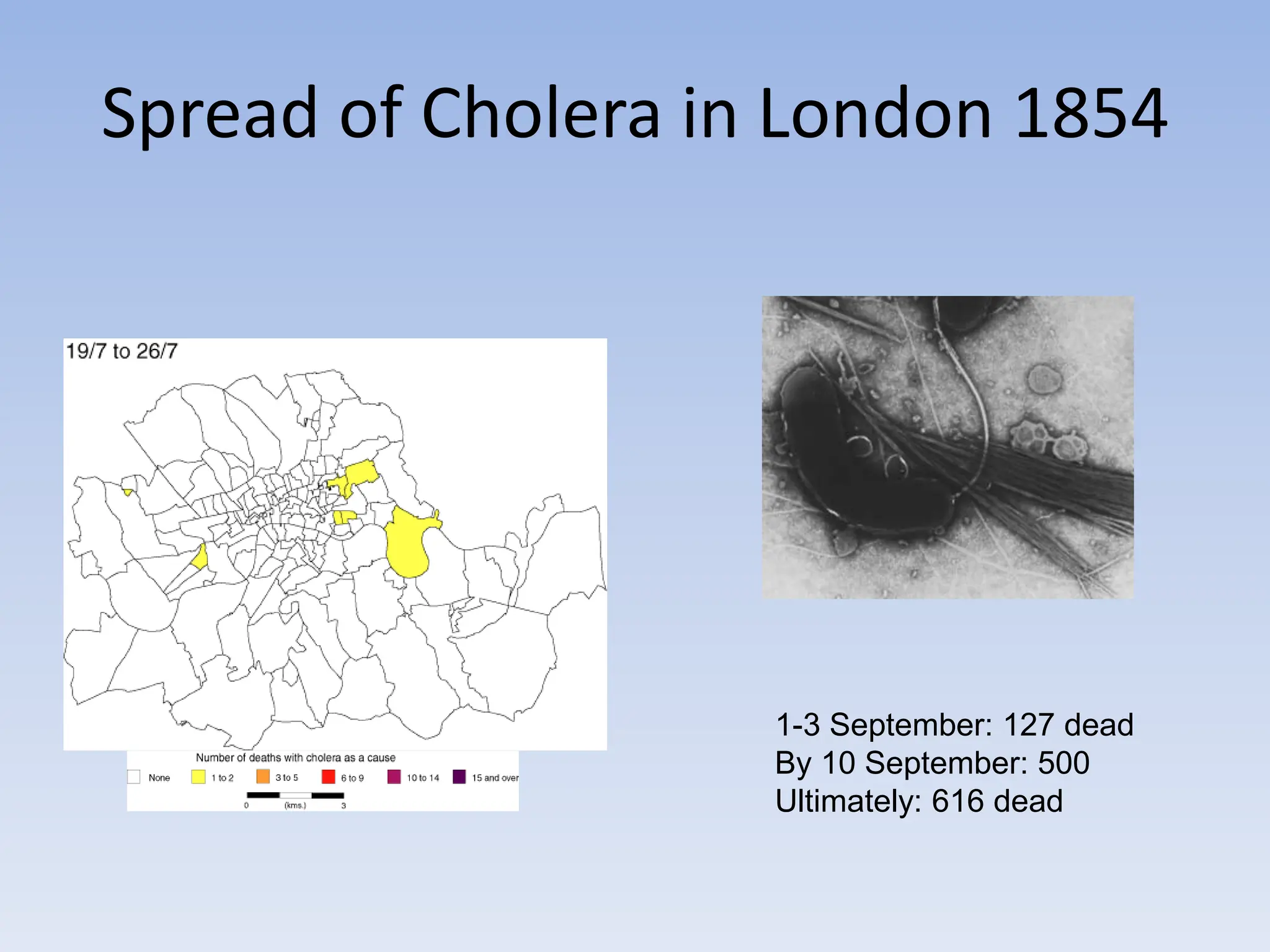
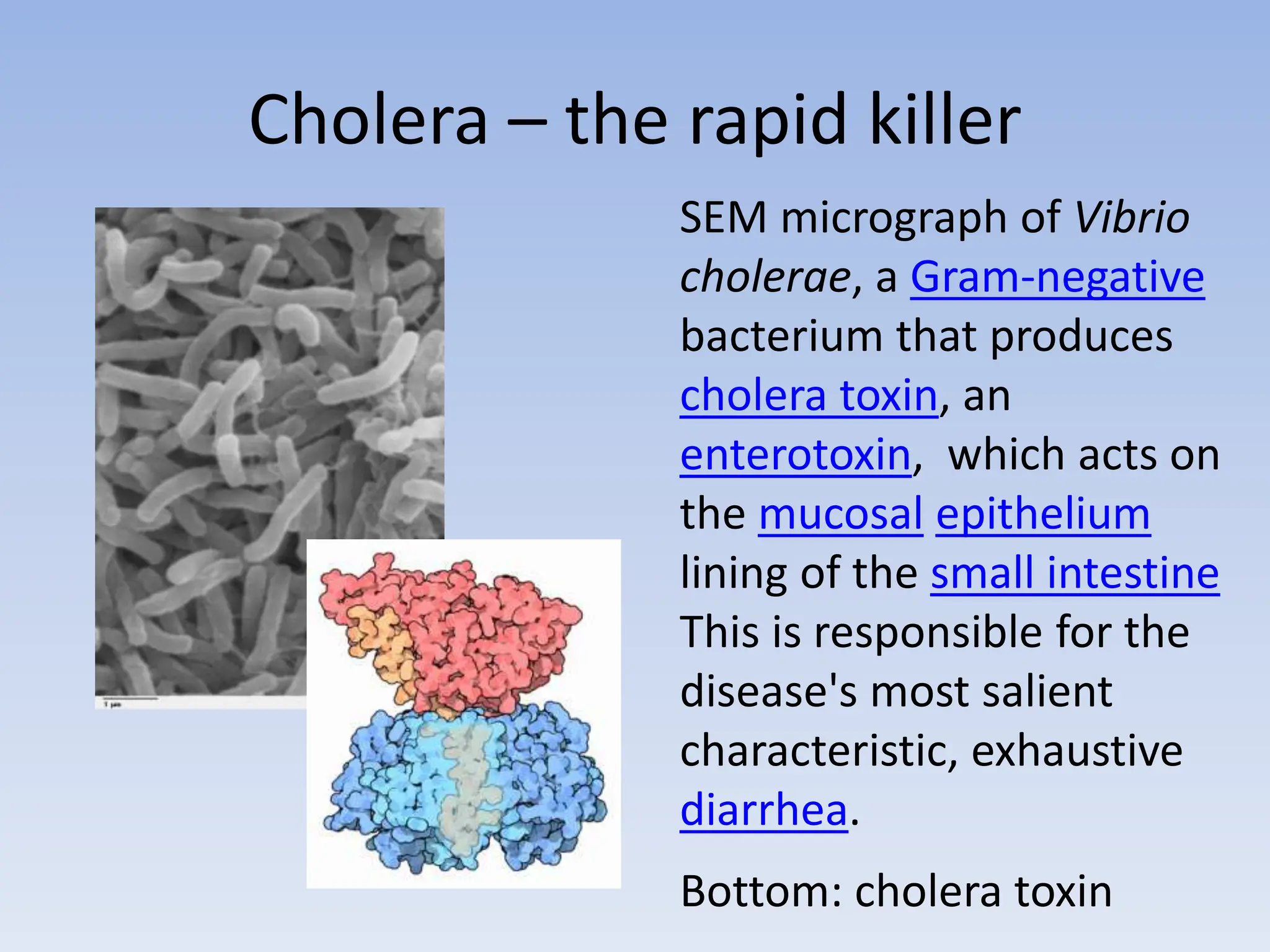
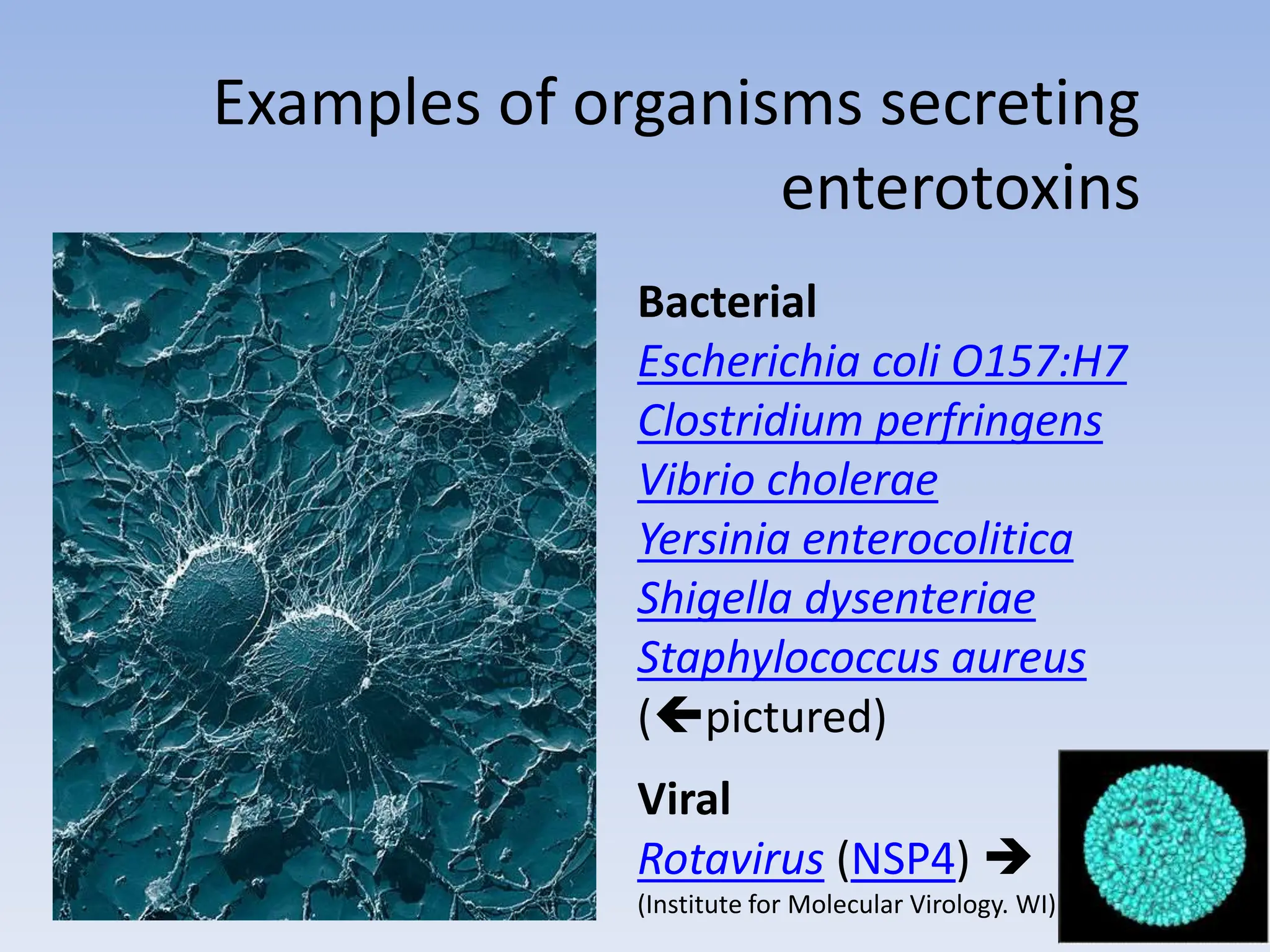
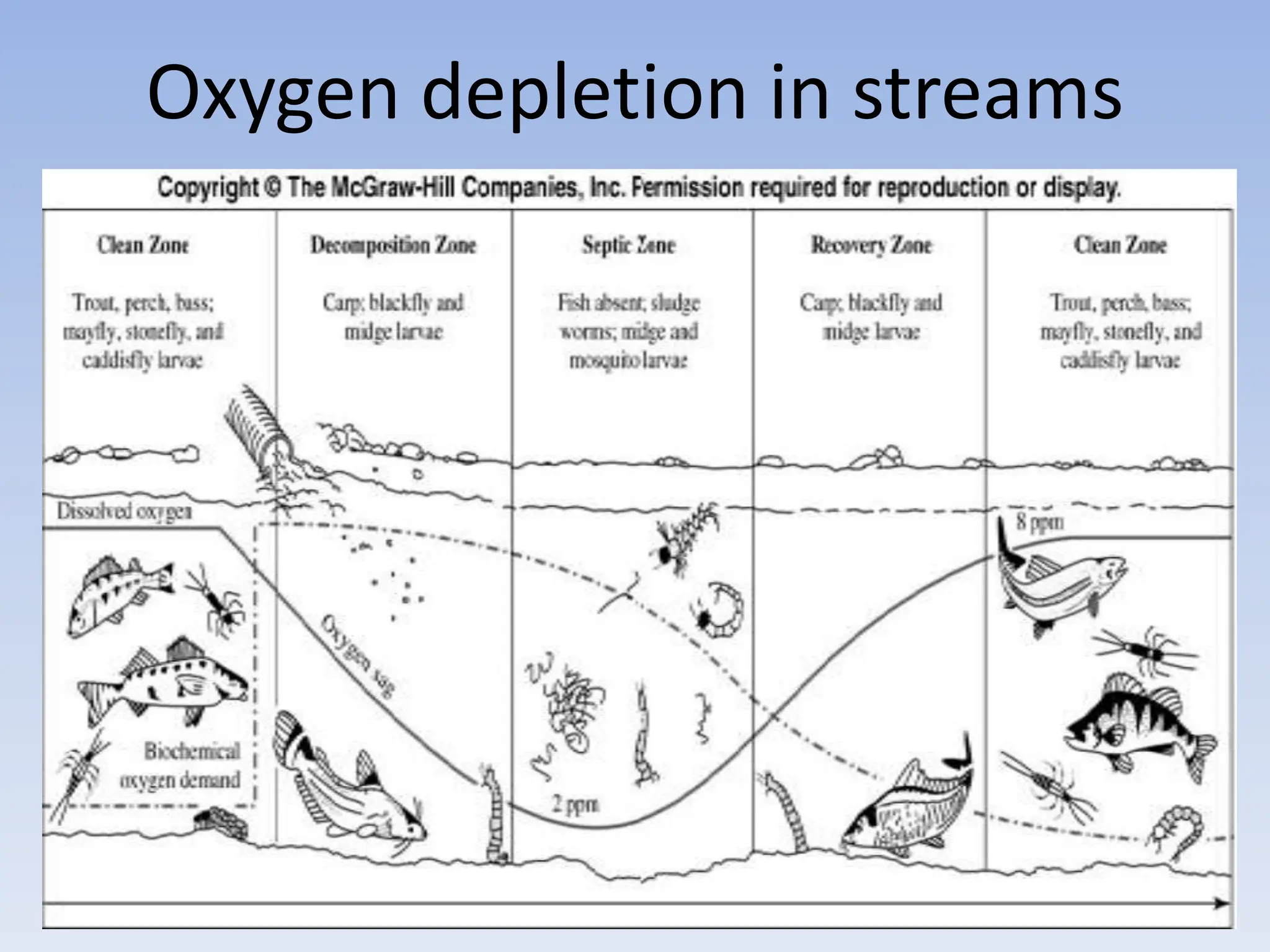
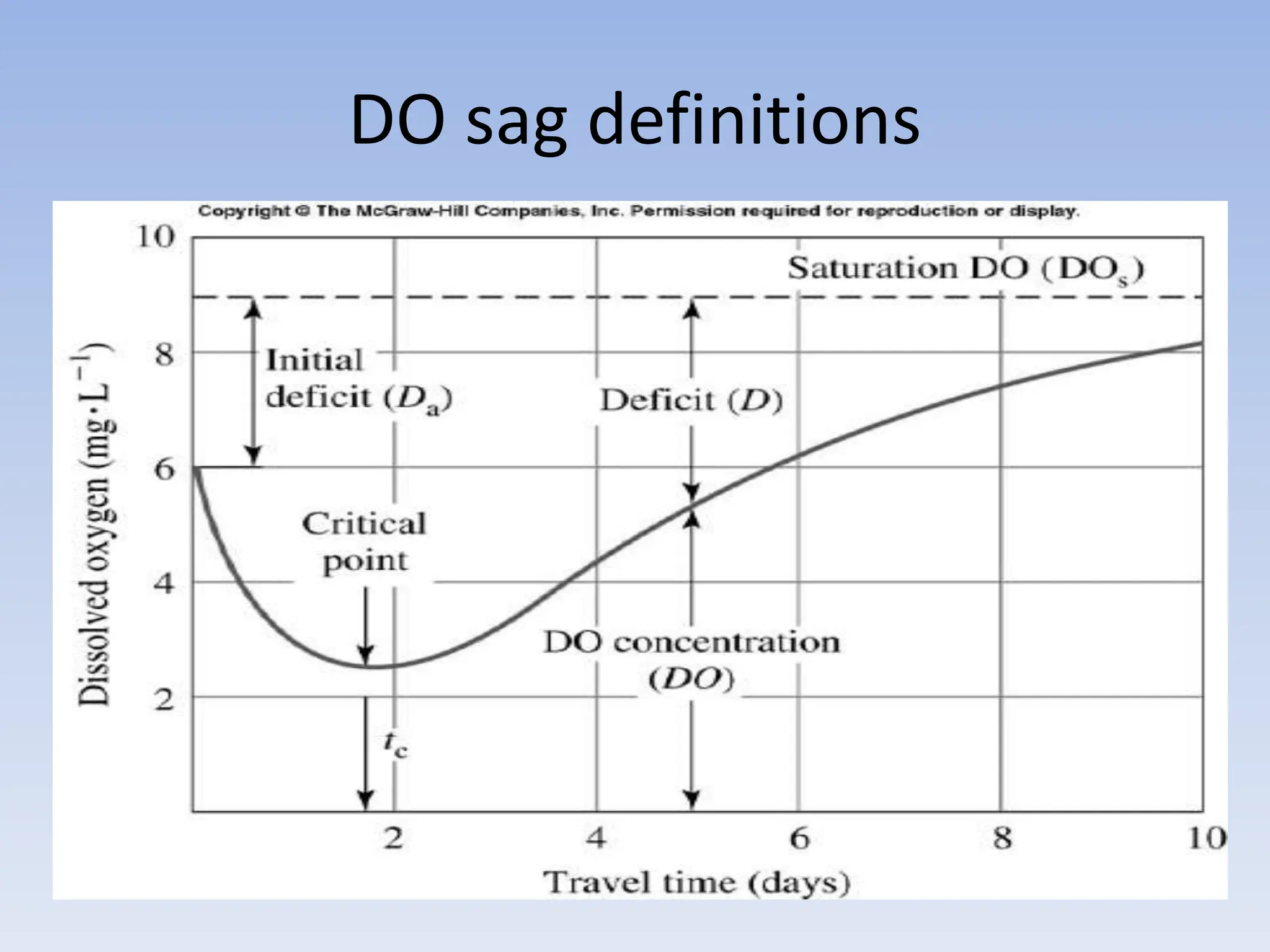
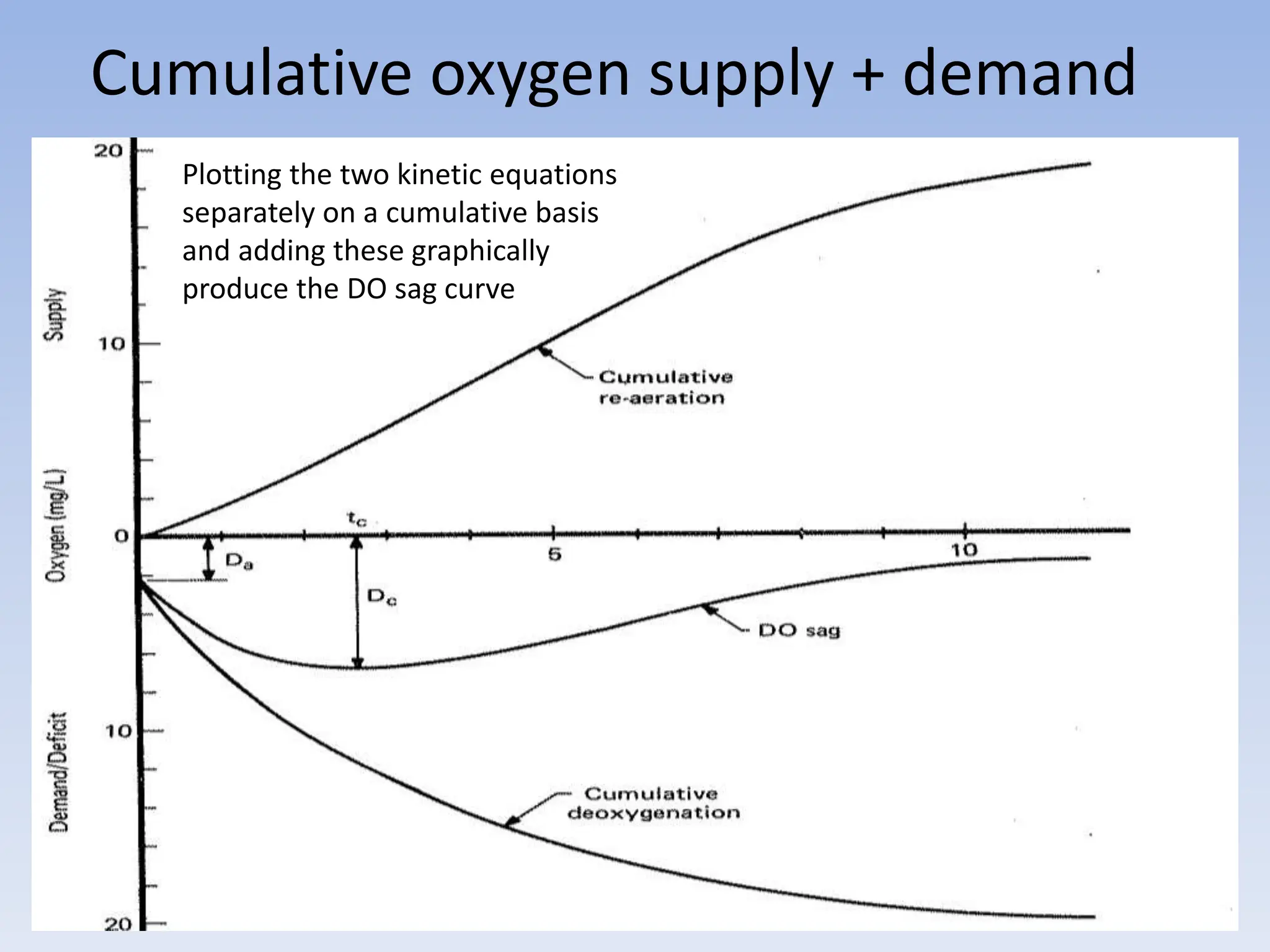
The document discusses the course BIOE 411/AE/CE/BRT 511, focusing on bioengineering principles, particularly in environmental contexts like wastewater treatment. It covers key topics such as dissolved oxygen measurement, biochemical oxygen demand (BOD) analysis, and the Streeter-Phelps model for understanding oxygen dynamics in water systems. The implications of oxygen depletion, pollution, and historical examples of disease outbreaks like cholera are also addressed to highlight the significance of these environmental factors.

1. INTRODUCTION TO
BIOENGINEERING II
BioE 411, AE/CE/BRT 511
J.(Hans) van Leeuwen
T.H. Kim

2. Instructor (33%)
Professor J. (Hans) van Leeuwen
from/of the Lions
• Born in Gouda, Netherlands
• Grew up in South Africa
• Lived in Australia for 7 years
• Lived in Ames for 11 years
Specialty: Environmental and Bioengineering
Industrial wastewater treatment and
product development based on waste materials

3. Research activities
Beneficiation of biofuel co-
products by cultivating fungi

4. Ozonation applications
Selective disinfection
Selective oxidation
Alcohol purification

5. Keeping exotic aliens out of our ports
ET
Zebra mussels

6. Human technological development
From scavengers…

7. Use of fire was the turning
point in the technological
development of humans
 leading to extended diet
 food preservation
 better hunting
 agriculture
 industry
Top of the food chain!
…to use of fire…
but, this ultimately led to…

8. …Overpopulation…

9. P
o
l
l
u
t
i
o
n
.
.

10. Pollution of a small stream

11. Consequence of pollution

12. …and ecological disasters

13. …and more disasters

14. Distribution of Earth’s water

15. Dangers lurking in water

16. Pollution from informal housing

17. Waterborne diseases
Map by Lord
John Snow of the
cholera outbreak
in London in
1854 – the Broad
Street Epidemic.
This is considered
the root of
epidemiology.

18. Spread of Cholera in London 1854
1-3 September: 127 dead
By 10 September: 500
Ultimately: 616 dead

19. Cholera – the rapid killer
SEM micrograph of Vibrio
cholerae, a Gram-negative
bacterium that produces
cholera toxin, an
enterotoxin, which acts on
the mucosal epithelium
lining of the small intestine
This is responsible for the
disease's most salient
characteristic, exhaustive
diarrhea.
Bottom: cholera toxin

20. Examples of organisms secreting
enterotoxins
Bacterial
Escherichia coli O157:H7
Clostridium perfringens
Vibrio cholerae
Yersinia enterocolitica
Shigella dysenteriae
Staphylococcus aureus
(pictured)
Viral
Rotavirus (NSP4) 
(Institute for Molecular Virology. WI)

21. Dissolved oxygen
Importance Why is oxygen in water important?
Dissolved oxygen (DO) analysis measures the amount of
gaseous oxygen (O2) dissolved in an aqueous solution.
Oxygen gets into water by diffusion from the surrounding air, by
aeration (rapid movement), and as a product of photosynthesis.
DO is measured in standard solution units such as
milligrams O2 per liter (mg/L), millilitres O2 per liter
(ml/L), millimoles O2 per liter (mmol/L), and moles
O2 per cubic meter (mol/m3).
DO is measured by way of its oxidation potential
with a probe that allows diffusion of oxygen into it.
The saturation solubility of oxygen in wastewater can be expressed as
Cs =  (0.99)h/88 x 482.5/(T + 32.6)
For example, in freshwater in Ames at 350m and 20°C, O2 saturation
is 8.8 mg/L. (Check for yourself, with  = 1)

22. BOD
Biochemical oxygen demand or BOD is a procedure for determining the
rate of uptake of dissolved oxygen by the organisms in a body of water
BOD measures the oxygen uptake by bacteria in a water sample at a
temperature of 20°C over a period of 5d in the dark. The sample is diluted
with oxygen saturated de-ionized water, inoculating it with a fixed aliquot
of microbial seed, measuring the (DO) and then sealing the sample to
prevent further oxygen addition. The sample is kept at 20 °C for five days,
in the dark to prevent addition of oxygen by photo-synthesis, and the
dissolved oxygen is measured again.
The difference between the final DO and initial DO is the BOD or, BOD5.
Once we have a BOD5 value, it is treated as just a concentration in mg/L
BOD can be calculated by:
Diluted: ((Initial DO - Final DO + BOD of Seed) x Dilution Factor
BOD of seed (diluted activated sludge) is measured in a control: just
deionized water without wastewater sample.
Significance: BOD is a measure of organic content and gives an indication
on how much oxygen would be required for microbial degradation.

23. Oxygen depletion in streams

24. DO sag definitions

25. Cumulative oxygen supply + demand
Plotting the two kinetic equations
separately on a cumulative basis
and adding these graphically
produce the DO sag curve

26. Streeter-Phelps Model*
Mass Balance for the Model
Not a Steady-state situation
rate O2 accum. = rate O2 in – rate O2 out + produced – consumed
rate O2 accum. = rate O2 in – 0 + 0 – rate O2 consumed
Kinetics
Both reoxygenation and deoxygenation are 1st order
* Streeter, H.W. and Phelps, E.B. Bulletin #146, USPHS (1925)

27. Kinetics* for Streeter-Phelps Model
• Deoxygenation
L = BOD remaining at any time
dL/dt = Rate of deoxygenation equivalent to rate of BOD removal
dL/dt = -k1L for a first order reaction
k1 = deoxygenation constant, f’n of waste type and temp.
*See Kinetics presentation if unfamiliar with the mathematical processing
kL
dt
L
d


]
[
 


C
C
t
dt
k
L
dL
0 0
kt
kt
e
L
L
e
L
L
or
kt
L
L 






 0
0
0
ln

28. Developing the Streeter-Phelps
Rate of reoxygenation = k2D
D = deficit in D.O.
k2 = reoxygenation constant*
 
 
2
3
2
1
)
20
(
2
1
2
025
.
1
9
.
3
H
v
k
T 

Where
– T = temperature of water, ºC
– H = average depth of flow, m
– ν = mean stream velocity, m/s
D.O. deficit
= saturation D.O. – D.O. in the water
Typical values for k2 at 20 °C, 1/d (base e) are as follows:
small ponds and back water 0.10 - 0.23
sluggish streams and large lakes 0.23 - 0.35
large streams with low velocity 0.35 - 0.46
large streams at normal velocity 0.46 - 0.69
swift streams 0.69 - 1.15
rapids and waterfalls > 1.15
There are many correlations for this.
The simplest one, used here, is from
O’Connor and Dobbins, 1958

29. Combining the kinetics
OR
Net rate of change of
oxygen deficiency, dD/dt
dD/dt = k1L - k2D
where L = L0e-k1t
dD/dt = k1L0e-k1t - k2D

30. Integration and substitution
t
k
o
t
k
t
k
o
e
D
e
e
k
k
L
k
D 2
2
1
)
(
1
2
1 






t
k
o
c
t
k
o
e
L
k
k
D
D
k
e
L
k
dt
dD
1
1
2
1
2
1 0
























o
o
c
L
k
k
k
D
k
k
k
k
t
1
1
2
1
2
1
2
)
(
1
ln
1
The last differential equation can be integrated to:
It can be observed that the minimum value, Dc is achieved when dD/dt = 0:
, since D is then Dc
Substituting this last equation in the first, when D = Dc and solving for t = tc:

31. Example: Streeter-Phelps
Wastewater mixes with a river resulting in a
BOD = 10.9 mg/L, DO = 7.6 mg/L
The mixture has a temp. = 20 C
Deoxygenation const.= 0.2 day-1
Average flow = 0.3 m/s, Average depth = 3.0 m
DO saturated = 9.1 mg/L
• Find the time and distance downstream at which the
oxygen deficit is a maximum
• Find the minimum value of DO

32. Solution…some values needed
• Initial Deficit
Do = 9.1 – 7.6 = 1.5 mg/L
(Now given, but could be calculated from proportional mix of river DO,
presumably saturated, and DO of wastewater, presumably zero)
• Estimate the reaeration constant:
k2 = 3.9 v½ (1.025T-20)½
H3/2
k2 = 3.9 x (0.3m/s)½ (1.02520-20)½
(3.0m)3/2
= 0.41 d-1

33. Solution…time and distance
days
L
k
k
k
DO
k
k
k
k
t
o
o
c
67
.
2
9
.
10
2
.
0
)
2
.
0
41
.
0
(
5
.
1
1
2
.
0
41
.
0
ln
)
2
.
0
41
.
0
(
1
)
(
1
ln
1
1
1
2
1
2
1
2




































m
days
day
s
s
m
vt
x c
c 300
,
69
67
.
2
/
400
,
86
/
3
.
0 




Note that the effects will be maximized almost 70 km downstream

34. Solution…maximum DO deficiency
mg/L
1
.
3
e
mg/L)
9
.
10
(
41
.
0
2
.
0 )
)(2.67days
(0.2day
2
1
1
1





 t
k
o
c e
L
k
k
D
The minimum DO value is 9.1-3.1 = 6 mg/L
Implication: DO probably not low enough for a fishkill, but if continued could
lead to species differentiation and discourage sensitives species like trout.
Note that this BOD could have been
calculated from mixing high-BOD
wastewater with zero or near-zero BOD