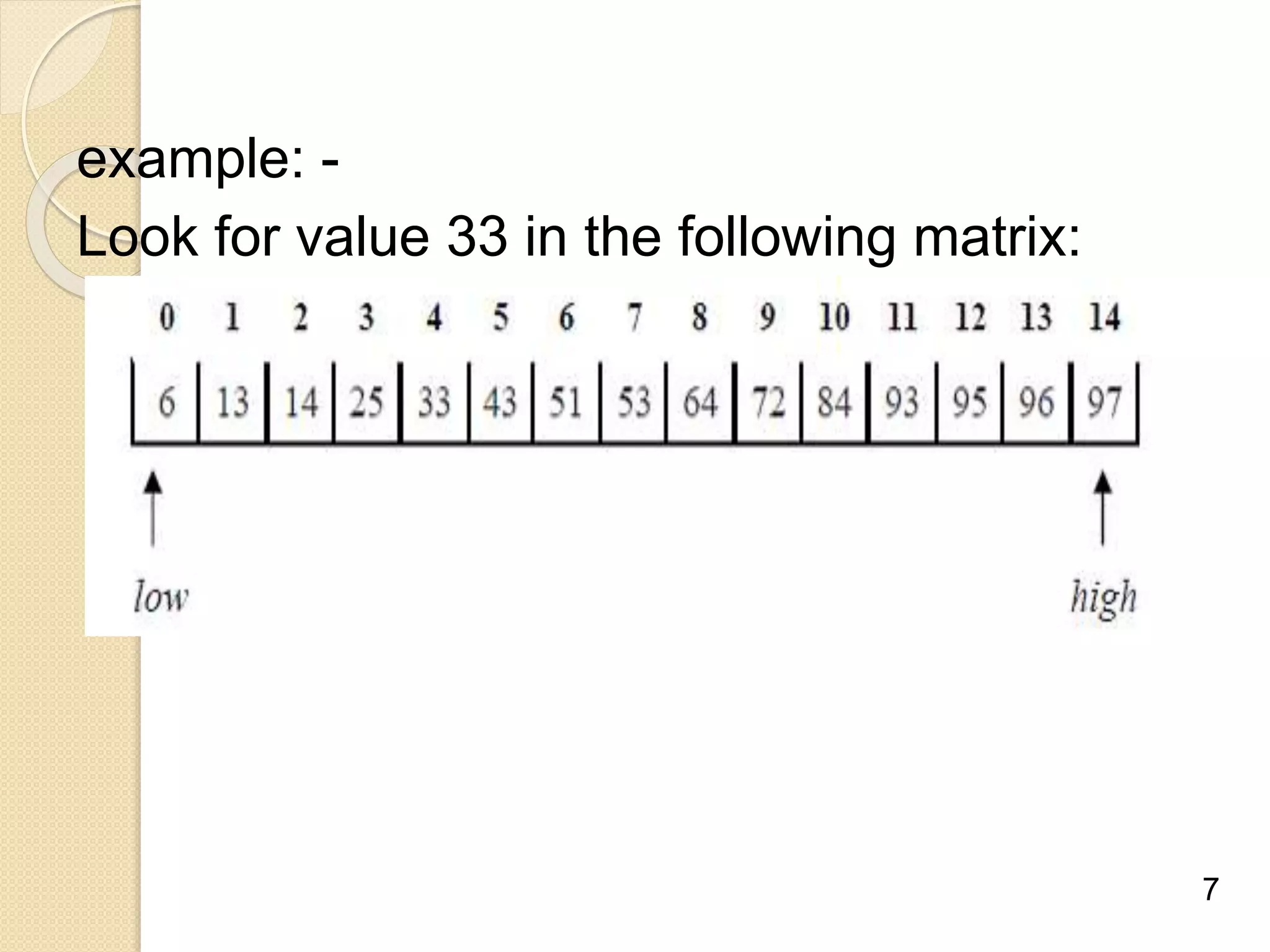
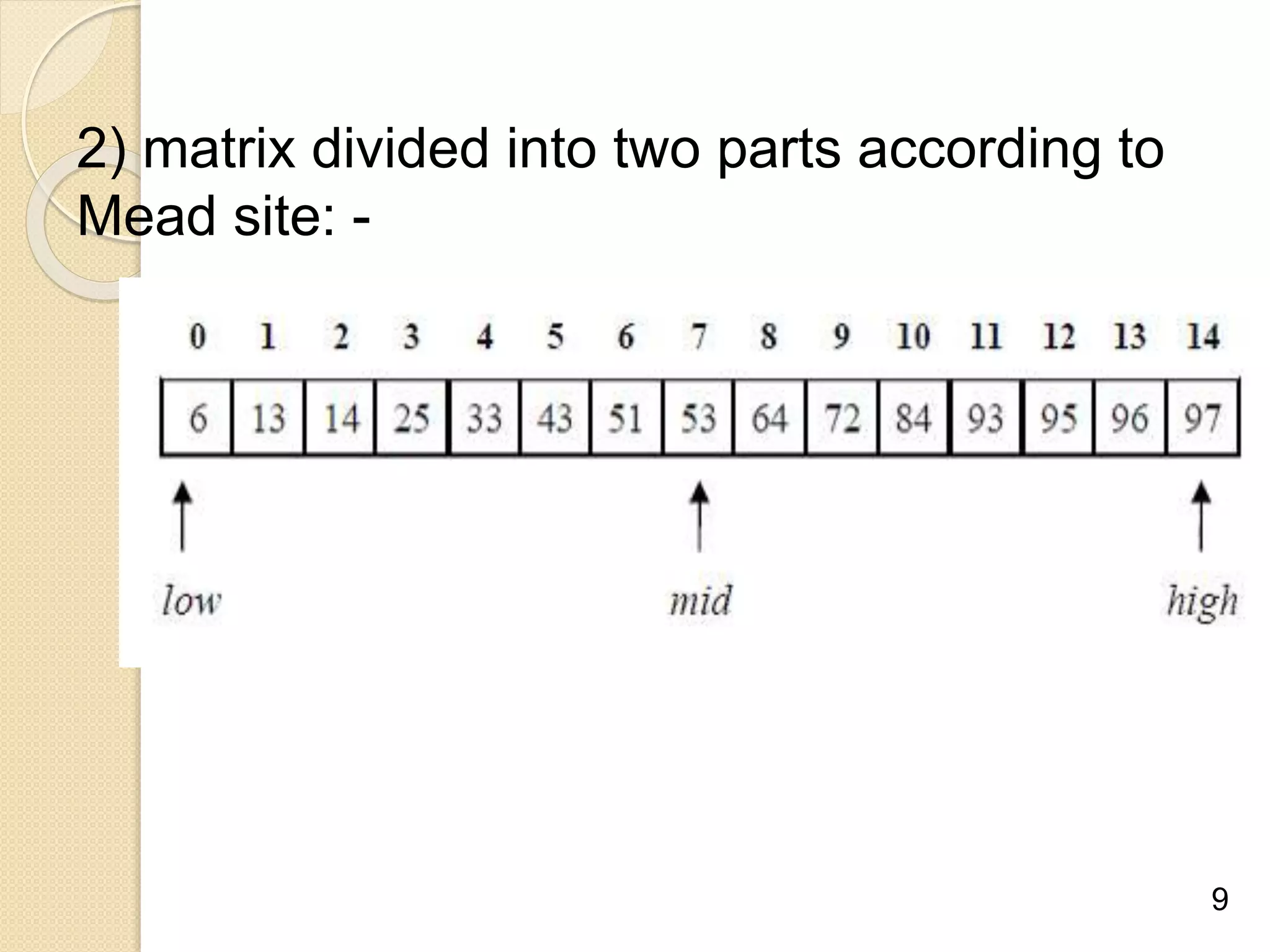
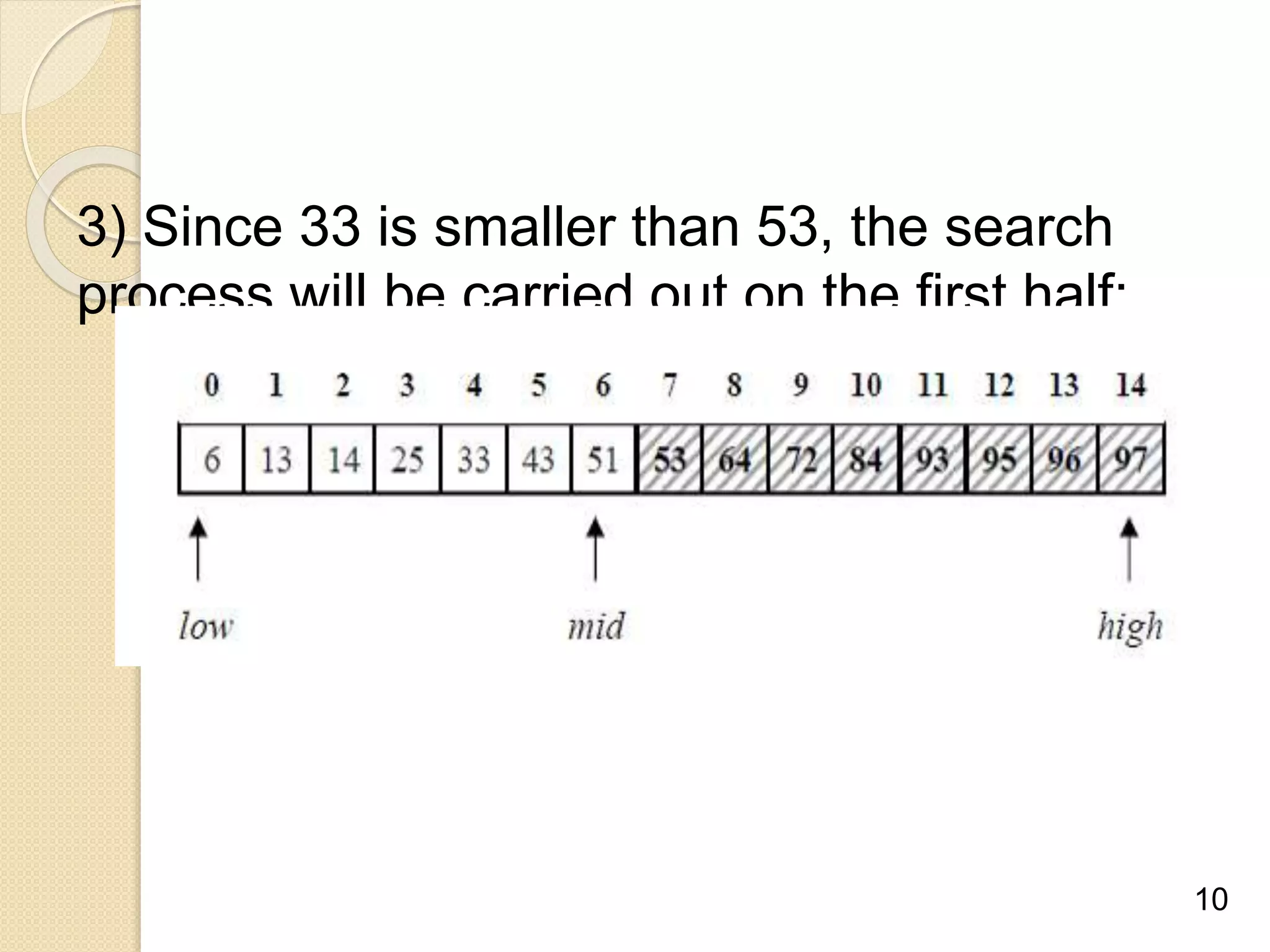
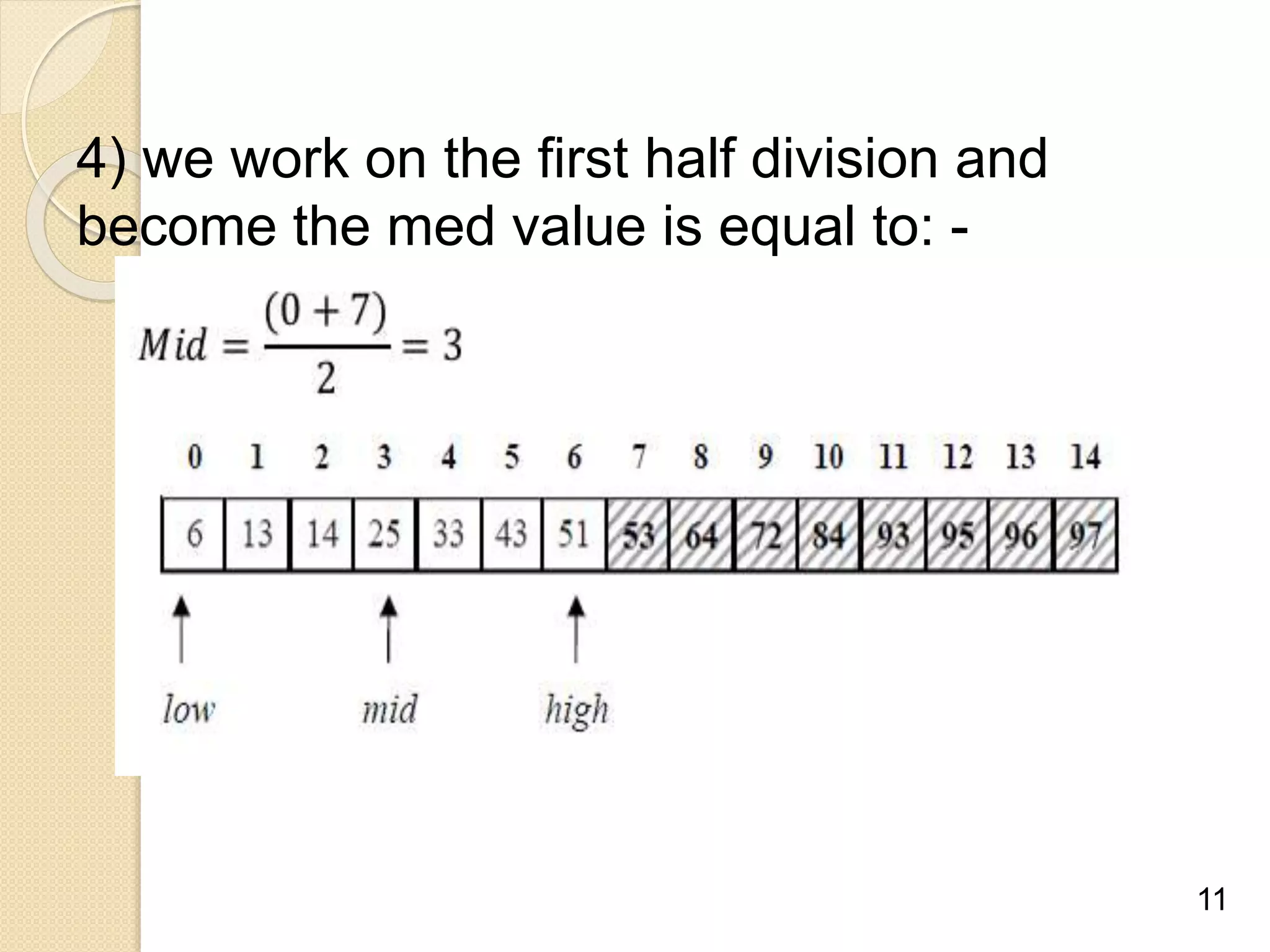
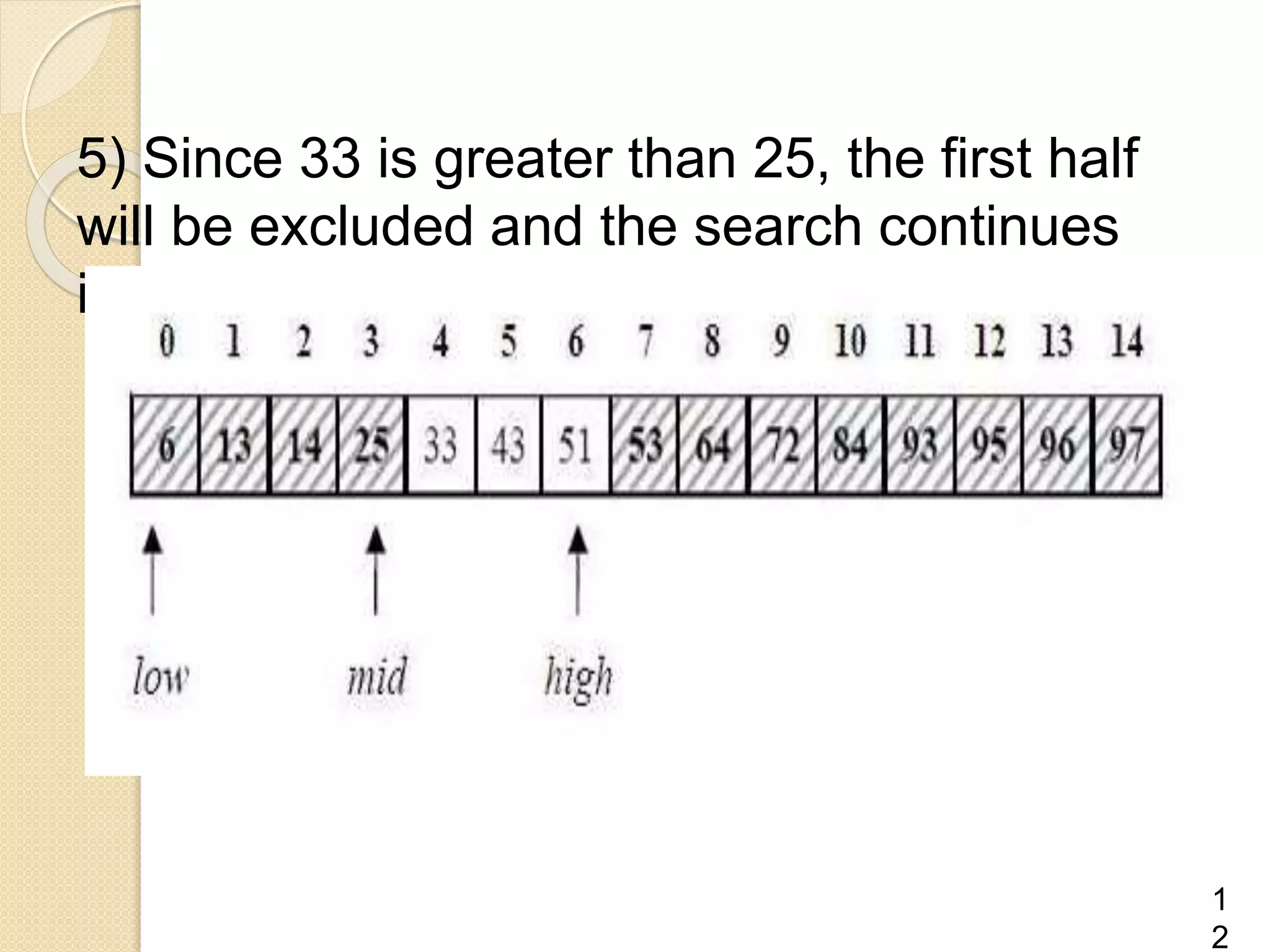
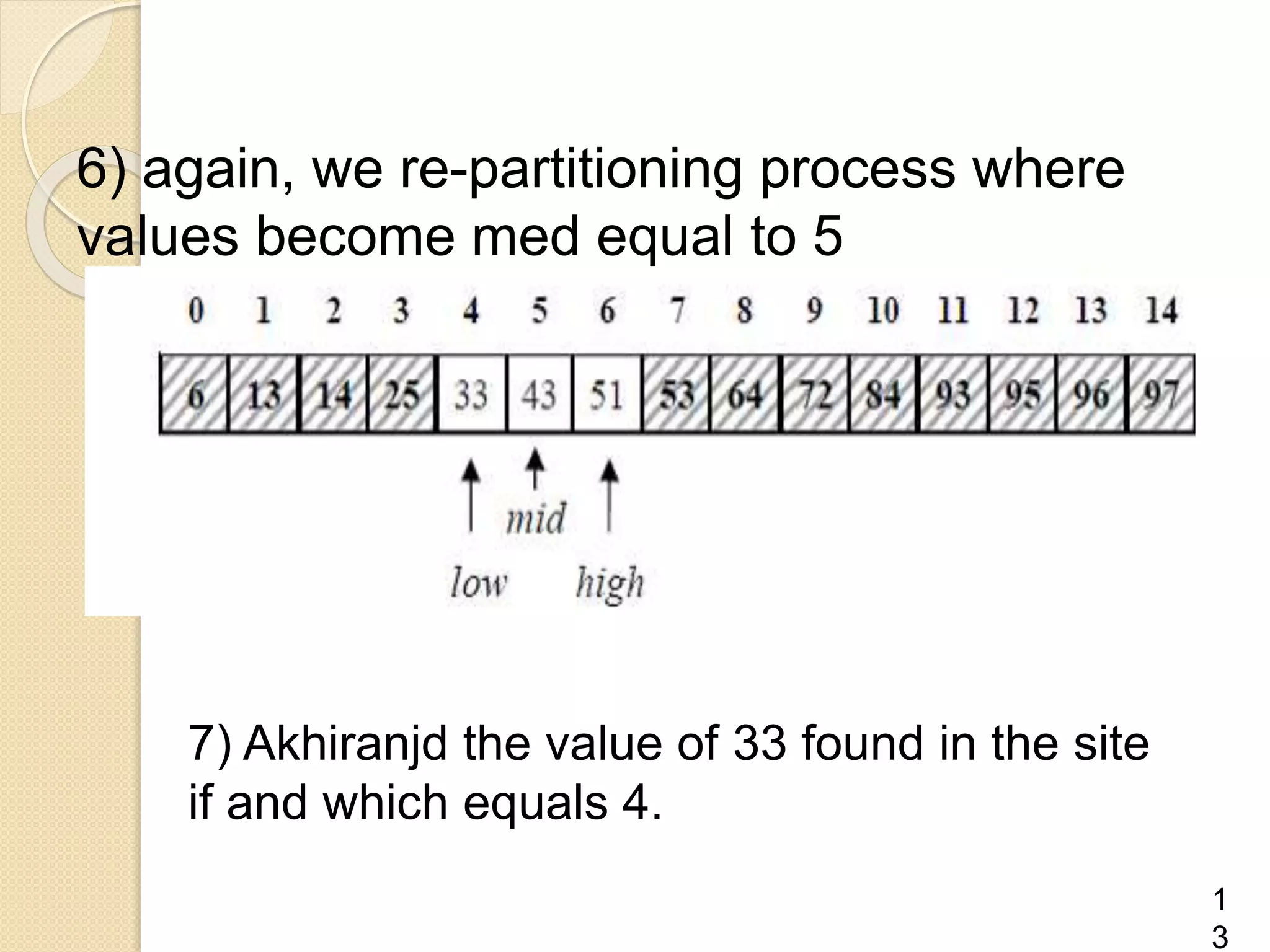
Binary search is an efficient algorithm for finding a target value within a sorted list or matrix. It works by repeatedly dividing the search space in half and eliminating half of the elements from consideration. The steps are: 1) sort the array, 2) set boundaries for search space, 3) check middle element and eliminate half based on comparison to target, 4) repeat until target is found or eliminated. It has best case performance of O(1) when finding the target on the first try, and worst case of O(log n) when searching the entire space. Binary search is commonly used to quickly find values in applications like computer games.

1. ‫الرحيم‬‫حمن‬‫الر‬‫هللا‬ ‫بسم‬
Bayan College
For
Science & Technology
Computer Science 6
Binary Search

2. binary search
Prepared by
:
Mohamed siddig
Tahani hassan
Rana seid

3. introduction
Problem:
Given a list of n numbers and q queries, find out whet
her each query is among the list of n numbers.
Analysis:
The solution is to use a linear search, where, for each
query k , we check each of then n numbers to see if k
is one of them. this o(n) algorithm will often be too slow.
we could use complicated data structures such as a set
or a hash table, but a much easier solution is to
implement a binary search
1

4. A binary search
is a divide-and-conquer .we algorithm divide the list in
half and search from only half of the list for future
iterations.
Objective: -
Find the value of the key to the matrix x .
The idea: -
This algorithm is based on binary search in the matrix
x. where the search begins from the element, which is
located in the center of the matrix, and every time I
compare it with the key so that, if the two values ​​are
equal,
this

5. indicates that the key is to find values ​​in the matrix, either if
the key value is less of the value of the item east settec
the search in the left part of the matrix and in the case of
adverse will be searched in the right part of the matrix,
and so on ... So we get a matrix consisting of one box a
value equal to the key or different about him.
3

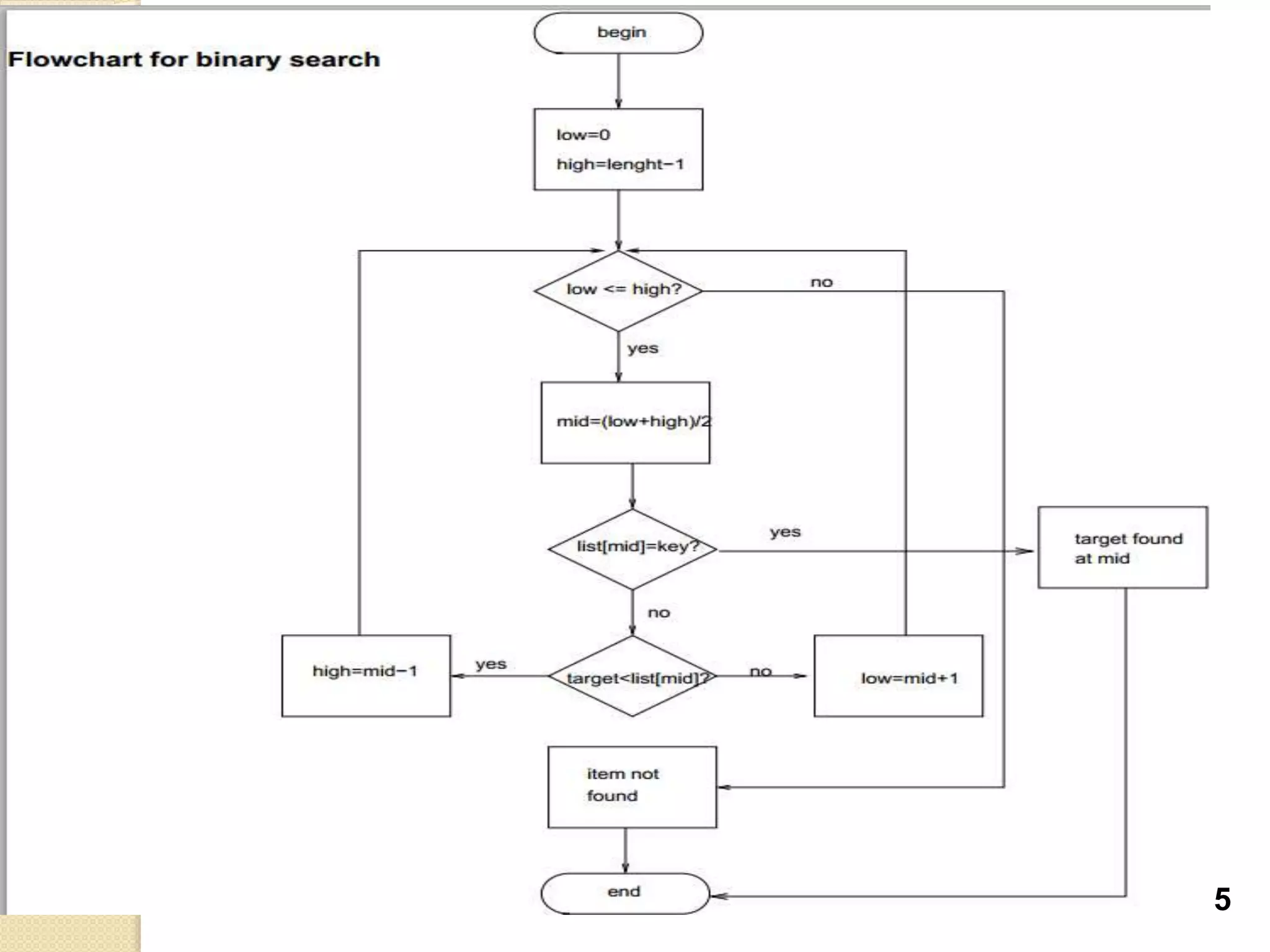
6. The steps of an algorithm:
1. sort array descending or ascending
2. Set low=0 and high=length-1
3. If low not smaller or not equal high go to 8:
4. Set middle =(low + high)/2
5. If target equal array [middle] go to 9
6. If target large then array[mid] set low =mid+1 t and go to 3.
7. If target smaller than array[mid] set high=mid-1 and go to 3
8. Print target not found and go 10
9. return middle
10. End function
4

7. The first way
5

8. Code :
int binary_search(int a[], int low, int high, int target)
{
while (low <= high)
{
int middle = (low + high)/2;
If(target==a[middle] )
return middle;
else if (target < a[middle])
high = middle - 1;
else if (target > a[middle])
low = middle + 1;
}
return -1;
}
6

9. example: -
Look for value 33 in the following matrix:
7

10. Solution
1) define the middle of the matrix:
8

11. 2) matrix divided into two parts according to
Mead site: -
9

12. 3) Since 33 is smaller than 53, the search
process will be carried out on the first half:
10

13. 4) we work on the first half division and
become the med value is equal to: -
11

14. 5) Since 33 is greater than 25, the first half
will be excluded and the search continues
in the second half
1
2

15. 6) again, we re-partitioning process where
values ​​become med equal to 5
7) Akhiranjd the value of 33 found in the site
if and which equals 4.
1
3

16. Best case and worst case :
·The best case for a binary search is finding the
target item on the first look
.The worst case for a binary search is searching for
an item which is not in the data or in last look .
1
4

17. Application :
binary search is now used in 99% of 3D games
and applications
15

18. Reference:
https://www.princeton.edu
http://www.algolist.net
http://stackoverflow.com
1
6