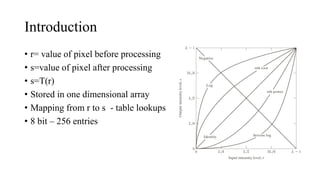
This document discusses various intensity transformation and spatial filtering techniques for digital images. It describes functions such as image negatives, log transformations, and power law (gamma) transformations that can compress or expand the dynamic range of pixel intensities. These transformations map input pixel values to output values using lookup tables to perform operations like inverting intensities, enhancing low-contrast regions, or adjusting image contrast. Log transformations specifically help narrow the range of low intensities while gamma correction is used to calibrate pixel values for display.

1. Intensity Transformation and
Spatial Filtering
19.08.2020
1:30 pm

2. Intensity Transformations Functions
• Image Negatives
• Log Transformations
• Power Law (Gamma) Transformations
• Piecewise-Linear Transformation Functions
• Contrast Stretching
• Intensity-level slicing
• Bit-plane slicing

3. Introduction
• r= value of pixel before processing
• s=value of pixel after processing
• s=T(r)
• Stored in one dimensional array
• Mapping from r to s - table lookups
• 8 bit – 256 entries

4. Image Negatives
• [0, L-1]
• s=L – 1 - r
• Negative – reversing the intensity
level
• Enhancing white or gray embedded
in dark region

5. Log Transformations
• s=clog( 1 + r)
• Narrow range of low intensity
• Inverse Log transformation
• Compresses the dynamic range of
images with large variations
• Pixel value in Large range – Fourier
Spectrum.
• Intensity detail may lost in Fourier
Spectrum

6. Power Law
• Gamma Transformation
• s=crγ
• Measurable output
• Input is 0 s=c(r+ε) γ
• Issue of display calibration
• Identity transformation – c = ϒ = 1
• Gamma Correction

7. Power Law
• Simply intensity map
• Gamma correction – straightforward
• S=r
1
2
.
5
= r0.4
• Input to the monitor
• Same intensity