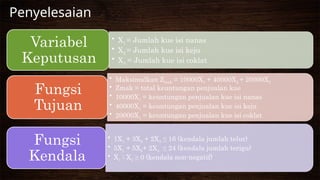
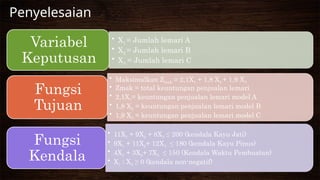
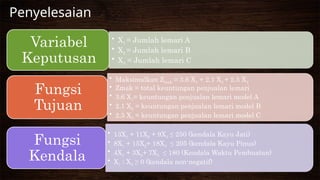
Dokumen ini membahas tentang pemodelan linear programming dengan metode simplex, termasuk konsep dasar, variabel keputusan, fungsi tujuan, dan kendala. Melalui contoh kasus, dijelaskan bagaimana menyusun model linear untuk mengoptimalkan produksi berbagai produk, serta mencari nilai maksimum keuntungan. Penjelasan juga mencakup langkah-langkah formulasi model dan penerapan pada masalah alokasi sumber daya terbatas.

1. IFK 332
PERMODELAN DAN SIMULASI
Pertemuan # 6 :
Model Linear Programming
Simplex Method
Dr. Erwin Hermawan, S.Si, M.Sc
LABORATORIUM GEOINFORMATIKA
PROGRAM STUDI TEKNIK INFORMATIKA
FAKULTAS TEKNIK & SAINS
UNIVERSITAS IBN KHALDUN

2. • Linear Programming /LP (Program Linear) merupakan teknik aplikasi dari
matematika yang dikembangkan oleh George B. Dantzig pada tahun 1947.
• LP merupakan sebuah model matematis yang digunakan untuk
mengalokasikan faktor produksi atau sumber daya yang jumlahnya terbatas
secara optimal, sehingga dapat seperti memaksimumkan keuntungan atau
meminimumkan biaya.
Pengantar Linear Programming

3. FUNGSI-FUNGSI DALAM LP
1. Variabel Keputusan
Variabel persoalan yang akan mempengaruhi nilai tujuan yang hendak dicapai.
2. Fungsi Tujuan (objective function)
Suatu fungsi Di mana tujuan yang hendak dicapai harus diwujudkan ke dalam sebuah fungsi
matematika linear, yang kemudian fungsi itu dimaksimumkan atau diminimumkan terhadap
kendala-kendala yang ada.
3. Fungsi Kendala (contrains or subject to)
Kendala dalam hal ini dapat diumpamakan sebagai suatu pembatas terhadap kumpulan
keputusan yang mungkin dibuat dan harus dituangkan ke dalam fungsi matematika linear
yang dihadapi oleh manajemen.
4. Fungsi Status (status function)
Fungsi yang menyatakan bahwa setiap variabel yang terdapat di dalam model programasi
linear tidak boleh negatif.

4. ASUMSI DASAR
1. Certainty
Angka yang diasumsikan dalam f.tujuan dan f.kendala secara pasti diketahui dan tidak
berubah selama waktu dipelajari.
2. Proporsionality
Alokasi sumber daya dengan goal yang ingin dicapai harus proporsional.
3. Additivity
Total dari semua aktivitas adalah sama dengan jumlah dari aktivitas individual
4. Divisibility
Jumlah produk yang akhirnya direkomendasikan dalam kondisi optimum, dapat berupa
pecahan bukan bilangan bulat.
5. Non-negatif variable
Semua variabel bukan negatif, bisa nol atau positif

5. FORMULASI MODEL
 Permasalahan: mencari nilai-nilai optimal (maksimum atau minimum) dari fungsi linear dengan kendala-
kendala tertentu
 Fungsi Tujuan: Fungsi linear yang dioptimumkan
 Fungsi Kendala: Fungsi-fungsi linear (lebih dari satu) yang harus dipenuhi dalam optimalisasi fungsi tujuan.
 Bentuk fungsi tujuan: persamaan atau pertidaksamaan
TAHAPAN FORMULASI MODEL
Formulasi model matematika, yang meliputi 3 tahap:
1. Tentukan variable keputusan dan nyatakan dalam simbol matematika
2. Membentuk suatu fungsi tujuan yang ditunjukkan sebagai suatu hubungan linear dari variable keputusan.
3. Menentukan semua kendala masalah dan mengekspresikan dalam persamaan atau pertidaksamaan yang
juga merupakan suatu hubungan linear dari variable keputusan.

6. 1. Fungsi Tujuan
Max/Min Z = c x + c x + ... + c
₁ ₁ ₂ ₂ nxn
2.Fungsi Kendala
a₁₁x₁ + a₁₂x₂ + … + a n
₁ xn < b₁
a x + a x + … + a nxn < b
₂₁ ₁ ₂₂ ₂ ₂ ₂
... ... ... ...
... ... ... ...
am x + am x + … + amnxn < bn
₁ ₁ ₂ ₂
3. Fungsi Status
x₁ ; x₂ ……………….. Xn > 0
FUNGSI MATEMATIKA LP

7. METODE-METODE DALAM LP

8. PERBEDAAN METODE SOLUSI LP

9. Kasus # 1 :
Sebuah perusahaan mebel akan membuat meja dan kursi. Setiap meja
membutuhkan 5 m2 kayu jati dan 2 m2 kayu pinus, serta membutuhkan waktu
pembuatan selama 4 jam. Untuk membuat sebuah kursi dibutuhkan 2 m2 kayu
jati, 3 m2 kayu pinus, dan 2 jam kerja. Dari penjualan sebuah meja didapat
keuntungan sebesar Rp. 120.000, sedangkan keuntungan untuk sebuah kursi
adalah Rp.80.000. Perusahaan ingin membuat mebel sebanyak- banyaknya,
tetapi terbatas dalam bahan baku dan jam pengerjaan. Dalam seminggu,
perusahaan hanya mampu mendapatkan 180 m2 kayu jati, 100 m2 kayu pinus,
serta hanya memiliki 80 jam kerja. Berdasarkan informasi tersebut :
a). Formulasikan permasalahan tersebut dalam model linier programming
b). Berapa banyak meja dan kursi yang harus diproduksi sehingga
perusahaan dapat memperoleh keuntungan sebanyak-banyaknya?

10. Penyelesaian
• X1 = Jumlah produksi meja
• X2 = Jumlah produksi kursi
Variabel
Keputusan
• Maksimumkan keuntungan : Zmax = 120.000X1 + 80.000X2
• Z = total keuntungan perbulan
• 120.000X1 = Keuntungan penjualan sebuah meja
• 80.000X2 = Keuntungan penjualan sebuah kursi
Fungsi
Tujuan
• 5X1 + 2X2 ≤ 180 (kendala ketersedian kayu jati dalam m2
)
• 2X1 + 3X2 ≤ 100 (kendala ketersedian kayu pinus dalam m2
)
• 4X1 + 2X2 ≤ 80 (kendala ketersediaan pengerjaan dalam jam)
• X1 ; X2 ≥ 0 (kendala non-negatif)
Fungsi
Kendala
a). Formulasi model linier programming

11. Penyelesaian
• Berdasarkan hasil optimasi dengan linier programming, perusahaan dapat
memproduksi secara maksimum dalam seminggu, meja (X1) sejumlah 5 unit
dan kursi (X2) sejumlah 30 unit. Keuntungan maksimum dalam seminggu yang
diperoleh perusahaan sebesar 3.000.000.

12. Seorang tukang kue mempunyai 16 kg telur dan 24 kg terigu. Ia akan membuat 3
macam kue isi dengan ketentuan sebagai berikut :
– 1 toples Kue isi nanas memerlukan 1 kg telur dan 2 kg terigu dengan keuntungan Rp
10.000/toples.
– 1 toples Kue isi keju memerlukan 3 kg telur dan 5 kg terigu dengan keuntungan Rp
40.000/toples.
– 1 toples Kue isi coklat memerlukan 2 kg telur dan 2 kg terigu dengan keuntungan Rp
20.000/toples.
• Berdasarkan informasi tersebut :
a). Formulasikan model linier programming
b). Berapa jumlah toples masing‐masing kue yang harus diproduksi agar
didapatkan keuntungan yang maksimal ?
Kasus # 2 :

13. Penyelesaian
• X1 = Jumlah kue isi nanas
• X2 = Jumlah kue isi keju
• X3 = Jumlah kue isi coklat
Variabel
Keputusan
• Maksimalkan Zmak = 10000X1 + 40000X2 + 20000X3
• Zmak = total keuntungan penjualan kue
• 10000X1 = keuntungan penjualan kue isi nanas
• 40000X1 = keuntungan penjualan kue isi keju
• 20000X1 = keuntungan penjualan kue isi coklat
Fungsi
Tujuan
• 1X1 + 3X2 + 2X3 ≤ 16 (kendala jumlah telur)
• 5X1 + 5X2+ 2X3 ≤ 24 (kendala jumlah terigu)
• X1 ; X2 ≥ 0 (kendala non-negatif)
Fungsi
Kendala

14. Penyelesaian
• Berdasarkan hasil optimasi dengan linier programming, tukang kue dapat
mengoptimalkan bahannya dengan membuat 4 toples kue isi keju dan 2 toples kue
isi coklat, dengan total keuntungan yang diperoleh sebesar 200.000

15. Sebuah Perusahaan ABC memproduksi 3 jenis model lemari A, B, dan C. Model lemari A membutuhkan
11 m2
kayu jati dan 9 m2
kayu pinus, serta membutuhkan waktu pembuatan selama 240 Menit. Model
lemari B membutuhkan 9 m2
kayu jati dan 11 m2
kayu pinus, serta membutuhkan waktu pembuatan
selama 180 Menit. Model lemari C membutuhkan 8 m2
kayu jati dan 12 m2
kayu pinus, serta
membutuhkan waktu pembuatan selama 7 jam. Keuntungan yang didapatkan dari penjualan sebuah
lemari model A,B dan C berturut turut sebesar Rp 2,1 Juta, Rp 1.8 Juta dan Rp 1.9 juta.
Perusahaan ingin membuat lemari sebanyak - banyaknya, namun terbatas dalam bahan baku dan jam
pengerjaan. Dalam seminggu, perusahaan hanya mampu mendapatkan 200 m2 kayu jati, 180 m2 kayu
pinus, serta hanya memiliki 150 jam yang dialokasikan untuk waktu pembuatan. Berdasarkan informasi
tersebut :
• Berdasarkan informasi tersebut :
a). Formulasikan permasalahan tersebut dalam bentuk model linier programming
b). Berapa jumlah optimal lemari dari setiap model yang harus dibuat dan berapa
keuntungannya maksimum yang bisa diperoleh?
Kasus # 3 :

16. Penyelesaian
• X1 = Jumlah lemari A
• X2 = Jumlah lemari B
• X3 = Jumlah lemari C
Variabel
Keputusan
• Maksimalkan Zmak = 2,1X1 + 1,8 X2 + 1,9 X3
• Zmak = total keuntungan penjualan lemari
• 2,1X1= keuntungan penjualan lemari model A
• 1,8 X2 = keuntungan penjualan lemari model B
• 1,9 X3 = keuntungan penjualan lemari model C
Fungsi
Tujuan
• 11X1 + 9X2 + 8X3 ≤ 200 (kendala Kayu Jati)
• 9X1 + 11X2+ 12X3 ≤ 180 (kendala Kayu Pinus)
• 4X1 + 3X2+ 7X3 ≤ 150 (Kendala Waktu Pembuatan)
• X1 ; X2 ≥ 0 (kendala non-negatif)
Fungsi
Kendala

17. Penyelesaian
• Berdasarkan hasil optimasi dengan linier programming , jumlah optimum lemari yang
harus dib uat untuk memaksimumkan keuntungan adalah dengan membuat lemari A
sebanyak 16 buah dan Lemari C sebanyak 3 Buah dengan mendapatkan keuntungan
maksimum sebesar 39 Jta rupiah.

18. Penyelesaian
• Berdasarkan hasil optimasi dengan linier programming, tukang kue dapat
mengoptimalkan bahannya dengan membuat 4 toples kue isi keju dan 2 toples kue
isi coklat, dengan total keuntungan yang diperoleh sebesar 200.000

19. Penyelesaian
• X1 = Jumlah lemari A
• X2 = Jumlah lemari B
• X3 = Jumlah lemari C
Variabel
Keputusan
• Maksimalkan Zmak = 3.6 X1 + 2.1 X2 + 2.5 X3
• Zmak = total keuntungan penjualan lemari
• 3.6 X1= keuntungan penjualan lemari model A
• 2.1 X2 = keuntungan penjualan lemari model B
• 2.5 X3 = keuntungan penjualan lemari model C
Fungsi
Tujuan
• 13X1 + 11X2 + 9X3 ≤ 250 (kendala Kayu Jati)
• 8X1 + 15X2+ 18X3 ≤ 205 (kendala Kayu Pinus)
• 4X1 + 3X2+ 7X3 ≤ 180 (Kendala Waktu Pembuatan)
• X1 ; X2 ≥ 0 (kendala non-negatif)
Fungsi
Kendala

20. SEE U….NEXT WEEK