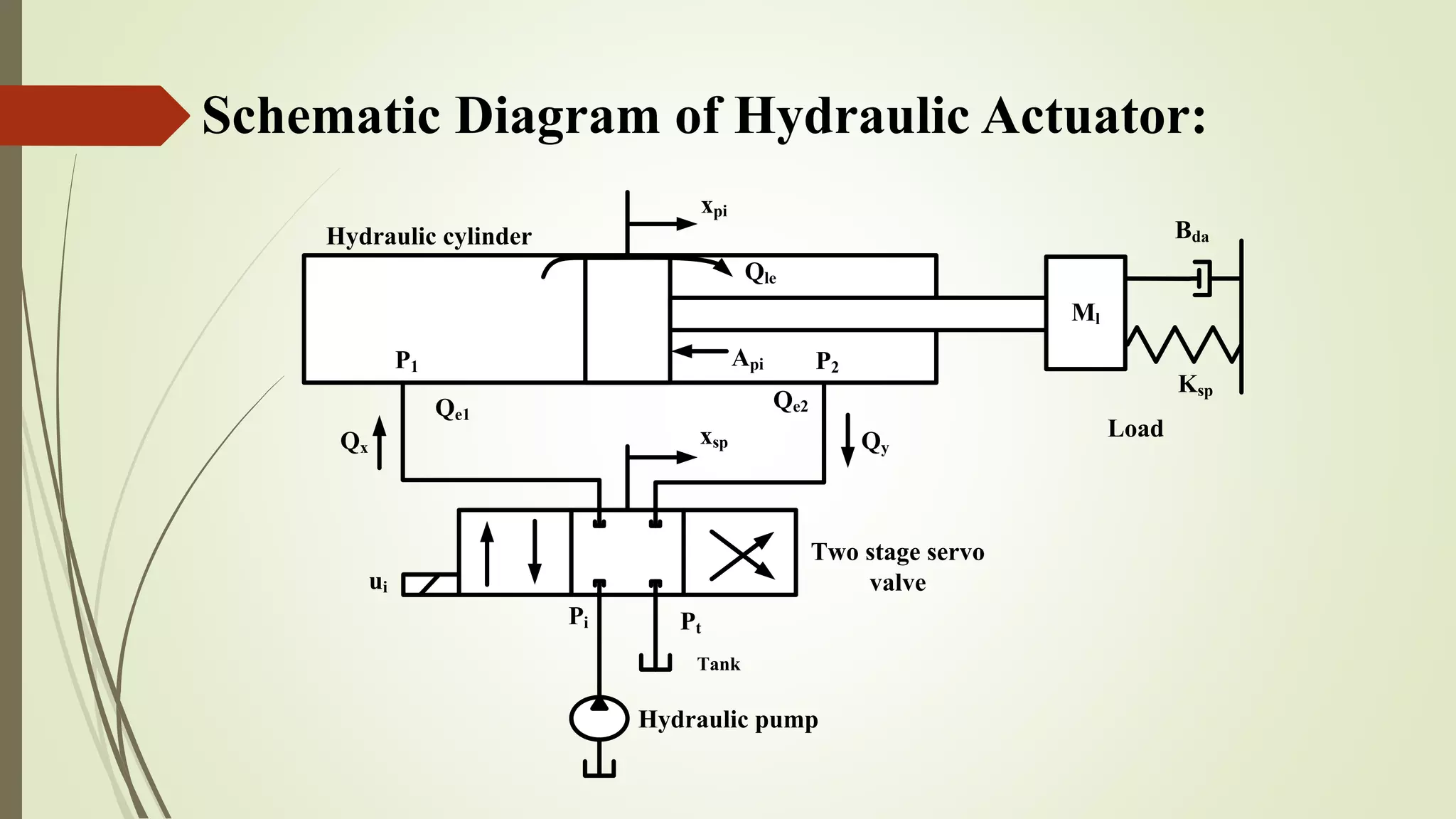
This document presents a hydraulic actuation system modeling using bond graph techniques. It summarizes the modeling of a two-stage servo valve and hydraulic actuator. The key steps are:
1. The two-stage servo valve and hydraulic actuator are modeled using bond graphs. Differential equations are derived from the bond graphs.
2. The differential equations are transformed into state-space form.
3. Simulation results are analyzed for the electro-hydraulic system model under conditions of underlap and critical lap servo.
The document outlines the component modeling using bond graphs, derivation of differential equations, and state-space representations to analyze the hydraulic actuation system dynamics.
















![Torque motor of Two Stage Servo Valve:
N N
SS
is
is
xfl
Permanent
Magnet
b
a
The relationship for Tmotor , Torque of the Motor for Two Stage Servo Valve [Merritt], is given by
𝑇 𝑚𝑜𝑡𝑜𝑟 = 𝐾 𝑚 θ 𝑓𝑙 + 𝐾𝑖 𝑖𝑠
Where, Tmotor = Torque of the motor
Km and Ki = Intensity control constant(Nm/A) and Rotational angle constant(Nm/rad)
θ 𝑓𝑙 = Flapper angle (rad)
is = input current (mA)](https://image.slidesharecdn.com/premnath-180813065437/75/Hydraulic-Actuation-System-modeling-for-developmental-Gas-Turbine-Engine-17-2048.jpg)