Download to read offline
Uploaded byHong Li
Hong_PhD
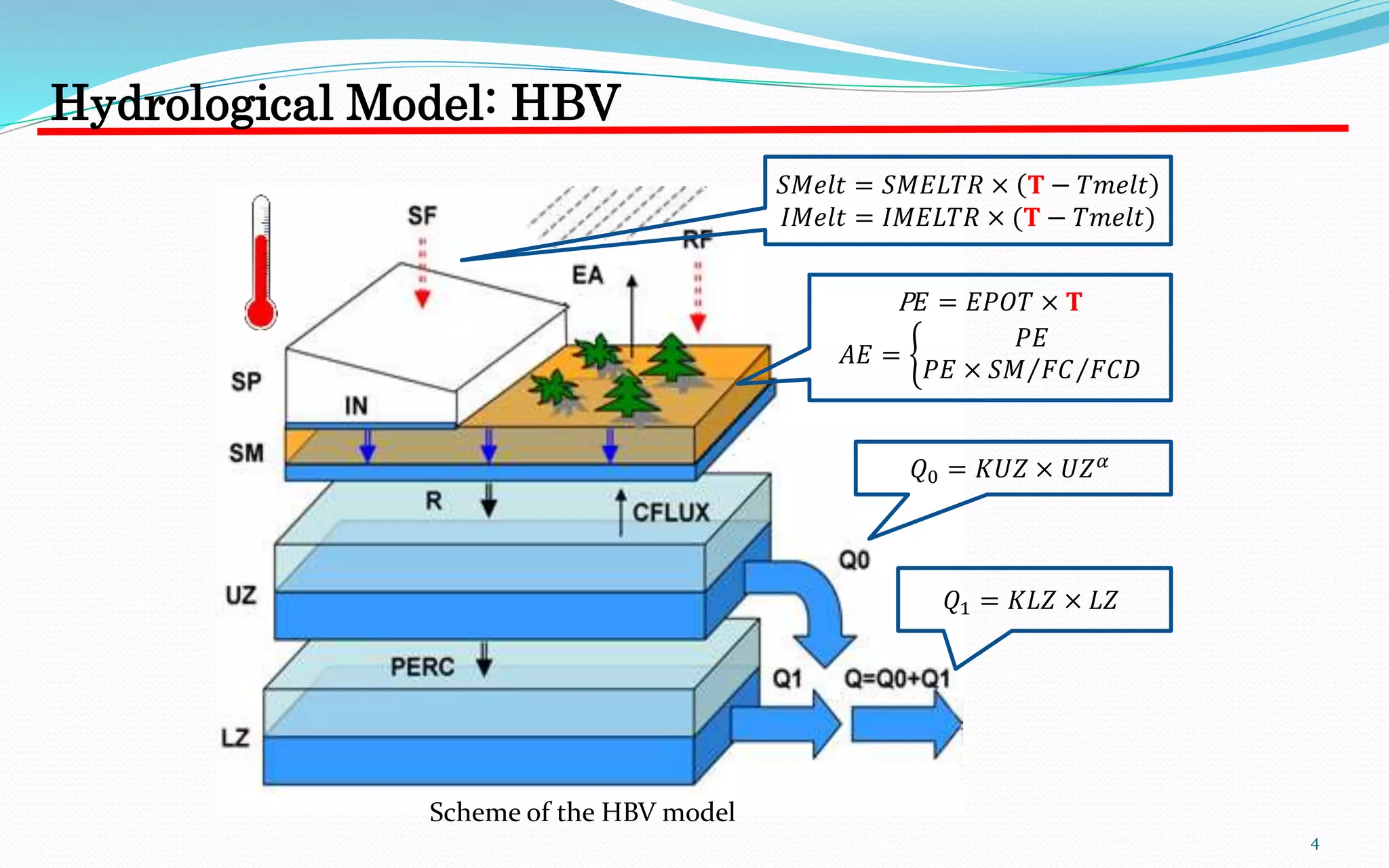
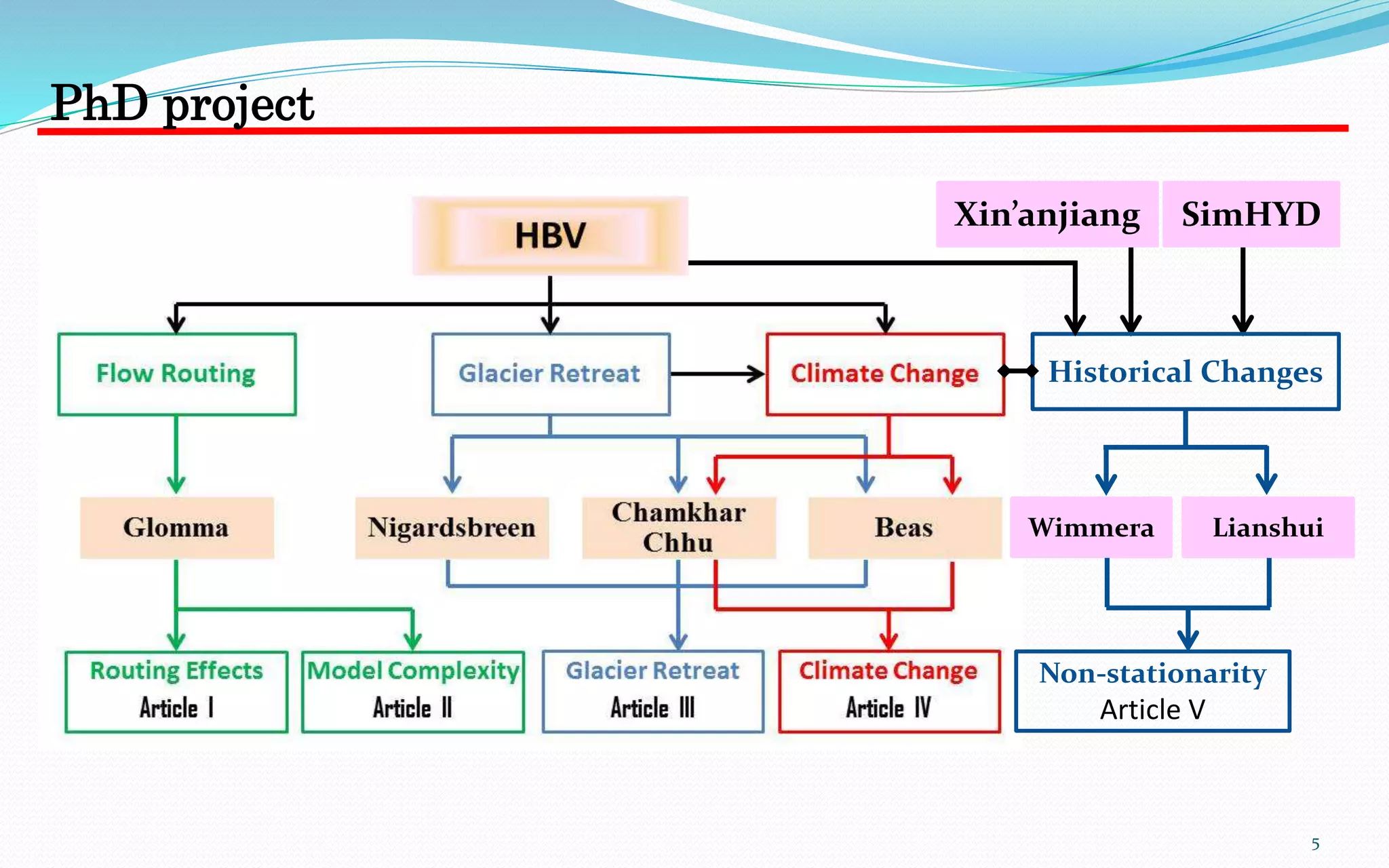
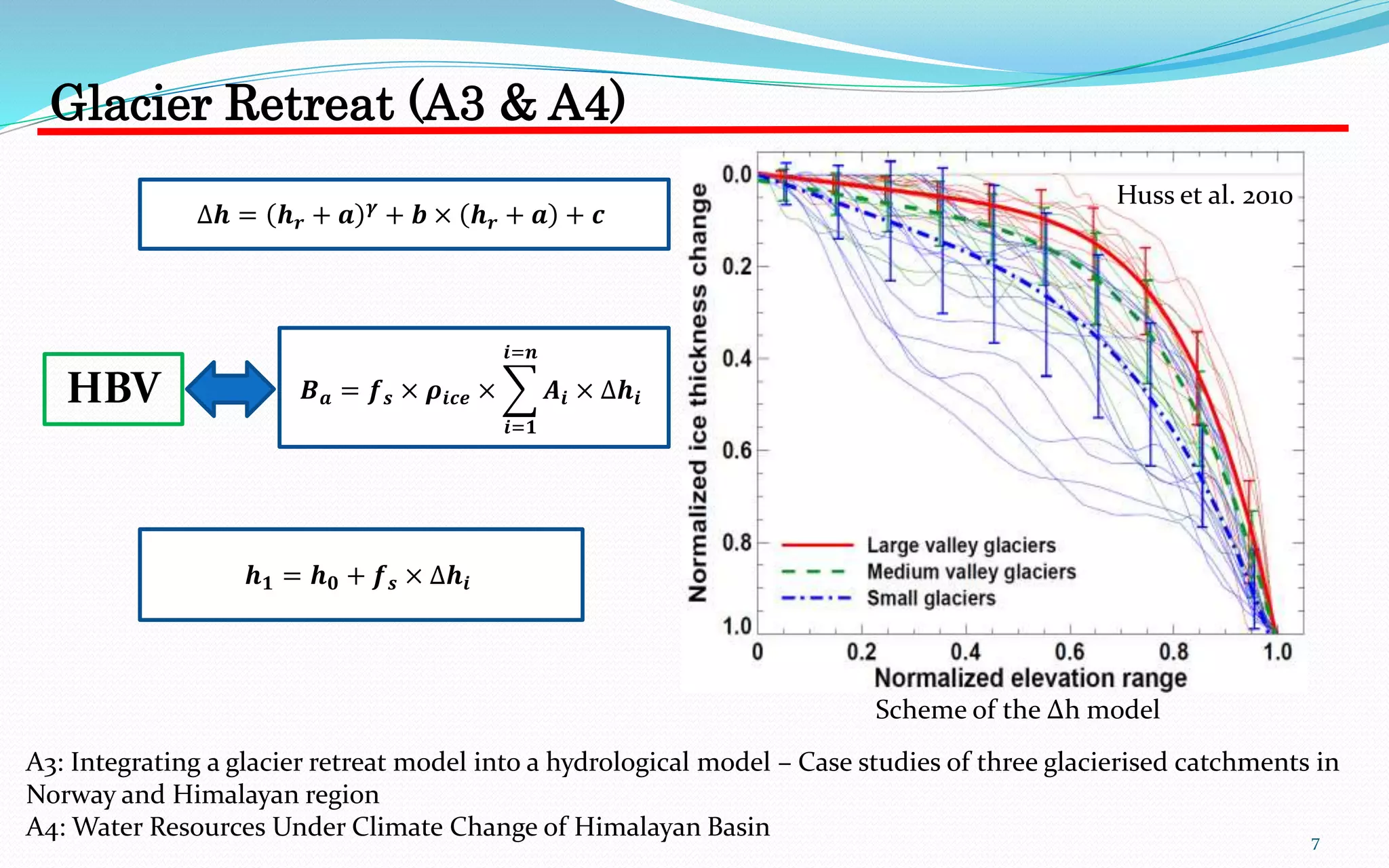
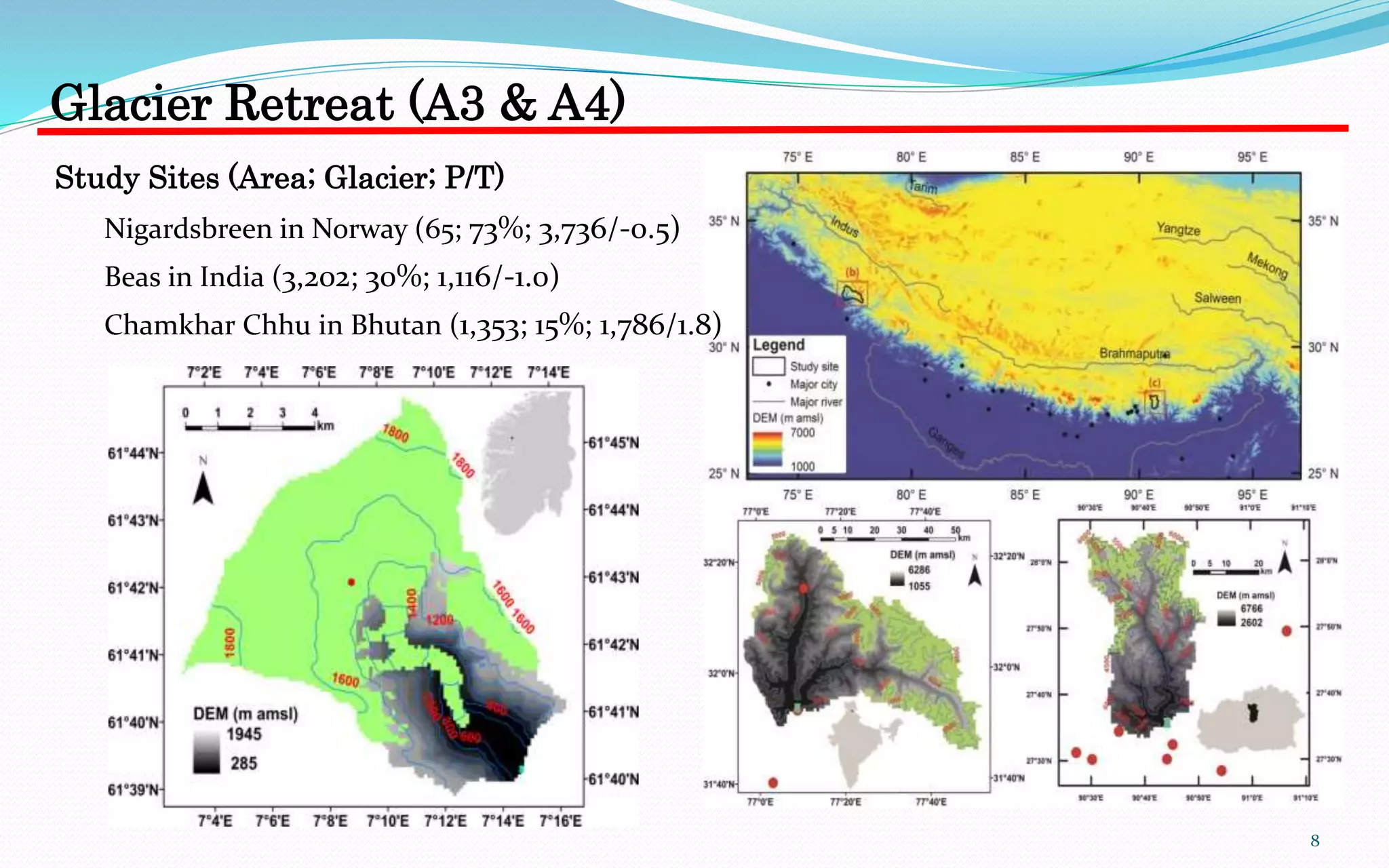
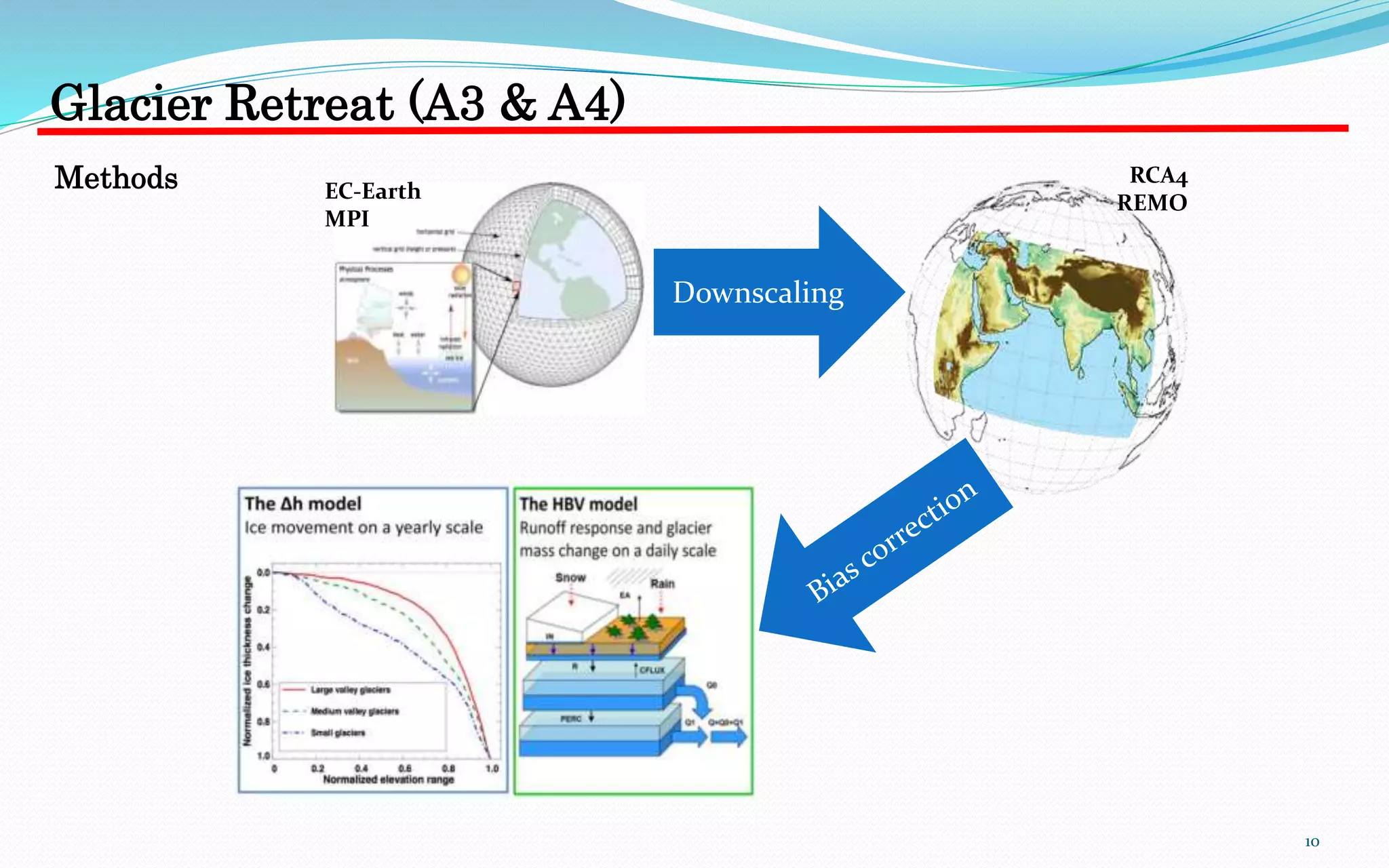
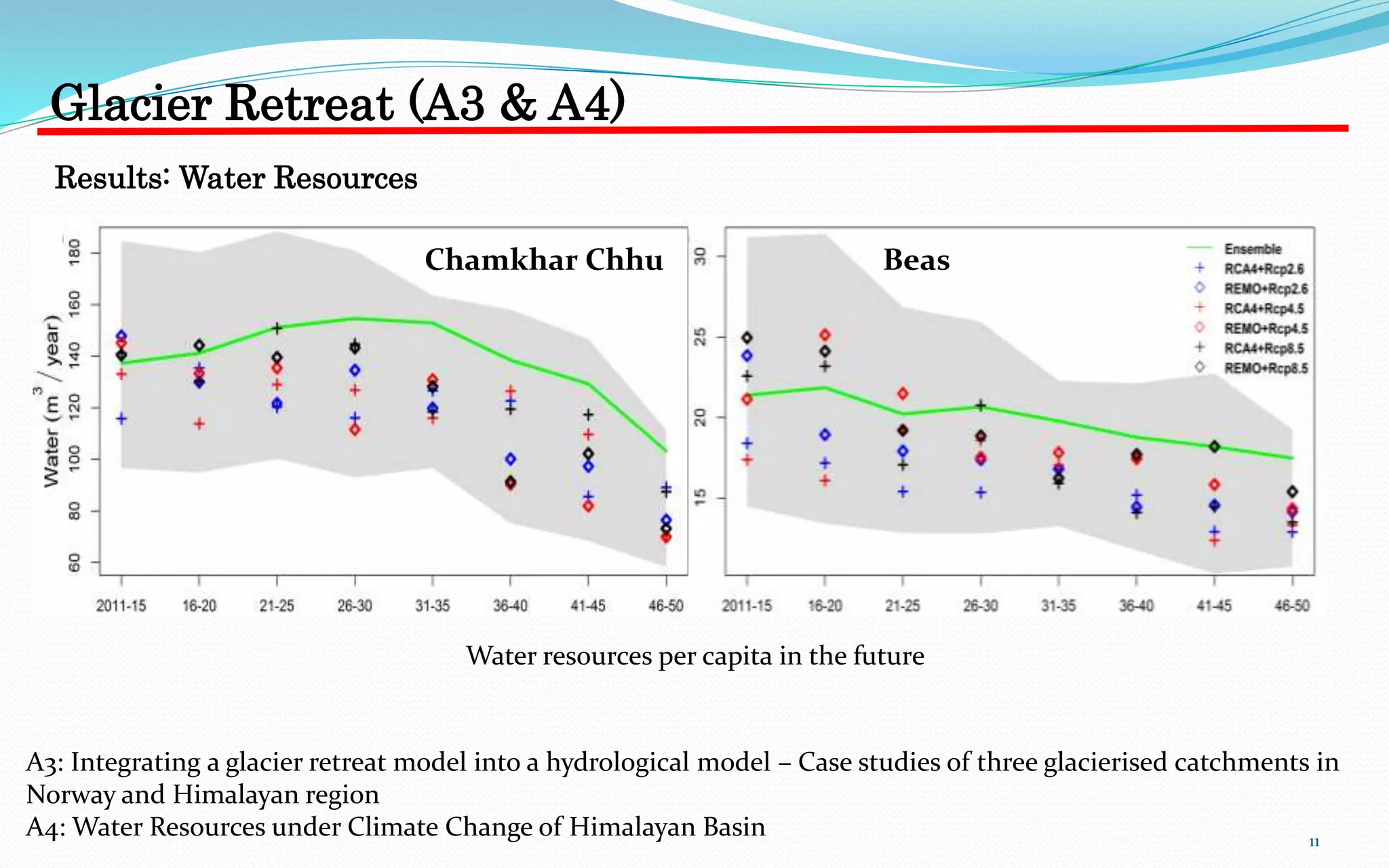
This document summarizes Hong Li's PhD research on integrating glacier retreat models into hydrological models. It includes: 1) Case studies of three glacierized catchments (in Norway and Himalayas) to assess model performance in simulating streamflow with and without a glacier retreat model. 2) Projections of future water resources in two Himalayan catchments (Chamkhar Chhu and Beas) under different climate change scenarios based on downscaled global climate model output. 3) An ongoing study examining the response of hydrological systems in India to climate change through climate modelling, hydrological modelling, and assessing changes in water resources.
Hong_PhD
- 1. 1 The highest goodnessis like water. Water benefits all things and does not compete. It stays in the lowly places which others despise. -------- Laozi 上善若水， 水善利万物而不争，处众人之所恶。 Hong Li 李红 hongli@met.no
- 2. 2005.09 – 2009.06B.Sc. China University of Mining & Technology 2009.09 – 2011.11 M.Sc. (Equivalent) Hohai (Rivers & Oceans) University 2011.12 – 2015.08 Ph.D. University of Oslo (NVE) 2015.07 – 2015.12 Scientist Norwegian Meteorological Institute Education 2
- 3. 3 Hydrological Model P: precipitation Q:streamflow; discharge; runoff E: evapotranspiration ∆S: change in water storage 𝑷 = 𝑸 + 𝑬 + ∆𝑺
- 4. 𝑆𝑀𝑒𝑙𝑡 = 𝑆𝑀𝐸𝐿𝑇𝑅× 𝐓 − 𝑇𝑚𝑒𝑙𝑡 𝐼𝑀𝑒𝑙𝑡 = 𝐼𝑀𝐸𝐿𝑇𝑅 × (𝐓 − 𝑇𝑚𝑒𝑙𝑡) P 𝐸 = 𝐸𝑃𝑂𝑇 × 𝐓 𝐴𝐸 = 𝑃𝐸 𝑃𝐸 × 𝑆𝑀 𝐹𝐶 𝐹𝐶𝐷 𝑄0 = 𝐾𝑈𝑍 × 𝑈𝑍 𝛼 𝑄1 = 𝐾𝐿𝑍 × 𝐿𝑍 4 Scheme of the HBV model Hydrological Model: HBV
- 5. 5 Wimmera Lianshui Non-stationarity Article V SimHYDXin’anjiang HistoricalChanges PhD project
- 6. 6 PhD project 1) Li,H. et al., 2014. Implementation and testing of routing algorithms in the distributed HBV model for mountainous catchments. Hydrology Research, 45(3), pp.322–333. doi: 10.2166/nh.2013.009. 2) Li, H. et al., 2015. How much can we gain with increasing model complexity with the same model concepts? Journal of Hydrology, 527, pp.858–871. doi: 10.1016/j.jhydrol.2015.05.044. 3) Li, H. et al., 2015. Integrating a glacier retreat model into a hydrological model – Case studies of three glacierised catchments in Norway and Himalayan region. Journal of Hydrology, 527, pp.656– 667. doi: 10.1016/j.jhydrol.2015.05.017. 4) Li, H. et al., 2015. Water Resources under Climate Change of Himalayan Basins. Water Resources Management, in press. 5) Li, H. et al., 2015. Stability of model performance and parameter values on two catchments facing changes in climatic conditions. Hydrological Sciences Journal, 60(7-8), pp. 1317-1330. doi: 10.1080/02626667.2014.978333.
- 7. ∆𝒉 = 𝒉𝒓 + 𝒂 𝜸 + 𝒃 × 𝒉 𝒓 + 𝒂 + 𝒄 𝒉 𝟏 = 𝒉 𝟎 + 𝒇 𝒔 × ∆𝒉𝒊 7 Scheme of the Δh model 𝑩 𝒂 = 𝒇 𝒔 × 𝝆𝒊𝒄𝒆 × 𝒊=𝟏 𝒊=𝒏 𝑨𝒊 × ∆𝒉𝒊HBV Huss et al. 2010 Glacier Retreat (A3 & A4) A3: Integrating a glacier retreat model into a hydrological model – Case studies of three glacierised catchments in Norway and Himalayan region A4: Water Resources Under Climate Change of Himalayan Basin
- 8. 8 Glacier Retreat (A3& A4) Study Sites (Area; Glacier; P/T) Nigardsbreen in Norway (65; 73%; 3,736/-0.5) Beas in India (3,202; 30%; 1,116/-1.0) Chamkhar Chhu in Bhutan (1,353; 15%; 1,786/1.8)
- 9. 9 𝑵𝑺𝑬 = 𝟏− 𝒊=𝟏 𝒊=𝒏 (𝑺𝒊 − 𝑶𝒊) 𝟐 𝒊=𝟏 𝒊=𝒏 (𝑶𝒊 − 𝑶) 𝟐 𝑹𝑴𝑬 = 𝒊=𝟏 𝒊=𝒏 𝑺𝒊 − 𝑶𝒊 𝒊=𝟏 𝒊=𝒏 𝑶𝒊 × 𝟏𝟎𝟎 R= 𝒊=𝟏 𝒊=𝒏 𝑶 𝒊− 𝑶 𝑺 𝒊− 𝑺 𝒊=𝟏 𝒊=𝒏 𝑶 𝒊− 𝑶 𝟐 𝒊=𝟏 𝒊=𝒏 𝑺 𝒊− 𝑺 𝟐 Basin Variable Criteria Calibration Validation Nigardsbreen Q NSE 0.90 0.90 RME 4.61 5.38 M R 0.90 0.92 Chamkhar Chhu Q NSE 0.87 0.85 RME -0.02 10.32 Beas Q NSE 0.65 0.73 RME 2.07 -22.38 Model performance in three basins Glacier Retreat (A3 & A4) Results
- 10.
- 11. 11 Chamkhar Chhu Beas Waterresources per capita in the future Glacier Retreat (A3 & A4) Results: Water Resources A3: Integrating a glacier retreat model into a hydrological model – Case studies of three glacierised catchments in Norway and Himalayan region A4: Water Resources under Climate Change of Himalayan Basin
- 12. 12 Ongoing … The responseof the hydrological system in India to climate change WP1 Climate modelling & Hydrological Modelling
Editor's Notes
- #2 As you may not know, there is an Chinese saying, ‘The highest goodness is like water.’ Water benefits all things and does not compete. It stays in the lowly places which others despise. Therefore it is near The Eternal. This philosophy is also shared by Ban Ki-moon, who is the eighth and current Secretary-General of the United Nations. He gave this four words to Obama as a gift for his 54 birthday. Obama seems very interested and curious. The importance of water and its lovely merits encourage me to study the water science as my career.
- #3 There are two parts. I will quickly go through my experiece and then we will focus on the research part. I studied in China for almost seven years before I came in Norway. In 2011, I started my PhD in University of Oslo and I got my degree in this August. The thesis title is ‘Hydrological modelling of Mountainous and glacierised regions under changing climate’. I will give more details in the Research part. Since this summer, I work in the Norwegian Meteorological Institute as a Scientist. I am doing regional climate modelling for Northern India. The purpose of my research is to study interactions between of glaciers and atmosphere.
- #4 The HBV model is a conceptual model. The main inputs are temperature and precipitation at a daily time step. Surface elevation, land use and soil data can be used to derive parameters. The model version used is from the NVE. It is a grid-based model. The model performs the water balance calculations for every grid. Runoff at basin outlet is the sum of all runoff from all grids. The evaporation is calculated based on the potential capacity and soil moisture. Snow and ice-melting is calculated by a degree-day method. The glacier extent is assumed constant. The runoff dynamics are simulated by two groundwater storages, the upper zone and lower zone. The upper zone is a non-linear reservoir and the lower zone is a linear reservoir. As we can see, there is a need to implement a routing module and upgrade the glacier representation.
- #5 The HBV model is a conceptual model. The main inputs are temperature and precipitation at a daily time step. Surface elevation, land use and soil data can be used to derive parameters. The model version used is from the NVE. It is a grid-based model. The model performs the water balance calculations for every grid. Runoff at basin outlet is the sum of all runoff from all grids. The evaporation is calculated based on the potential capacity and soil moisture. Snow and ice-melting is calculated by a degree-day method. The glacier extent is assumed constant. The runoff dynamics are simulated by two groundwater storages, the upper zone and lower zone. The upper zone is a non-linear reservoir and the lower zone is a linear reservoir. As we can see, there is a need to implement a routing module and upgrade the glacier representation.
- #6 This is the structure of the five papers. The flow routing is done on the Glomma basin, which is the largest basin in Norway. The HBV model with the glacier retreat model is tested on three glacier basins, the Nigardsbreen in Norway and two Basins in the Himalayas. The two Himalayan basins are also used in the forth paper, to project water resources for the future. The last paper is not included in my thesis, but published during my PhD study. The purpose is to compare three widely used hydrological models, HBV, Xin’anjiang and SimHYD on two basins with very different climate. First, I will introduce the HBV model, since it the basis.
- #7 The research part is about five papers. The first two papers are about flow routing in Norwegian basins. They are published in Hydrology Research and Journal of Hydrology. The third and fourth papers are implementing a glacier routine into the HBV model and using it in projecting water resources. The fifth one is to examine the stability of model performance and parameter values on two catchments, where significant hydrological changes were observed. At present, I am preparing a paper about my ongoing research in the Norwegian Meteorological Institute.
- #8 In many places, glaciers are reported to retreat due to warming climate. The static assumption about glacier extent is not valid anymore. The glacier retreat model is called delta h model. It based on the varying thinning rates over a glacier. The x-axis is the normalised elevation hr, from 0, the highest elevation, to 1, the lowest elevation. The y-axis is the normalised ice thickness change delta h, from 1, the largest change, to 0, the smallest change. For a dynamic stable glacier, the changes of surface elevation are larger at the low than the high. This can be described by a function of normalised elevation and four parameters, a, b, c and gamma. The total changes of a glacier by the glacier model is equal the mass change calculated by the HBV model. Thereby, the four parameters can be calibrated. The required data are initial ice thickness and surface elevation.
- #9 In total, three basins are used. The Nigardsbreen Basin is located western Norway. The basin has a small area, but with a large range of elevation and glacier coverage. The highest point is 1,957 m and the lowest in only 285 m. About 73% of the basin area is covered by ice. The mean annual air temperature is below zero and the mean annual precipitation reaches 3,736 millimetres per year, with a large amount falling in winter as snow. Streamflow is largely determined by melting of snow and ice in the warm period of the year. The data source is also the “SeNorge” 1 kilometer grid data. Since this basin is quite small and the model resolution is 100 meters. The areal mean value is assigned to a virtual station located at the center of the basin. Other data, such as discharge, annual mass balance data and elevation maps are from NVE. The Himalaya is one of the most sensitive regions to climate change. This area is still called a “white spot” in the IPCC Third Assessment Report. The Beas River lies in the west Himalaya. It is an important branch of the Indus River system. The area above the Bhuntar station is 3,202 square kilometres. The area in light green is occupied by permanent snow and glaciers. It is around 30 percent of the total area. The mean annual precipitation is 1,116 millimetres per year and the mean annual air temperature is -1.04 centigrade. There are three meteorological stations, shown by the red dots. Two of the stations are located in the selected area, one at the north valley and one at the outlet. The Chamkhar Chhu basin is located in central Bhutan. The basin area above the Kurjey station is 1,353 square kilometres. The northern part above 4,000 m is mainly covered by glaciers, account for 15 percent of the total area. The climate is strongly influenced by monsoon and it varies from the southeast to the northwest. The mean annual precipitation is 1,786 millimetres per year and the mean annual air temperature is 1.7 centigrade. The monsoon normally starts in June and lasts until early September. It brings significant amounts of rainfall and warm weather. There are seven weather stations; however none of them lies inside the basin. Their measurements are interpolated by the inverse distance weighting method considering elevation.
- #10 Among the three basins, only the Nigardsbreen has more than twenty years’ data. The model is calibrated in the first 12 years, and then is validated the following ten years. Other two basins are only calibrated for six, or seven years and validated for three or four years. The model is very accurate on the Nigardsbreen Basin. The model efficiency of discharge is higher than 0.9 as well as the glacier mass balance. No glacier data are available in the Chamkhar Chhu Basin, the efficiency is higher than 0.85. The low efficiency on the Beas Basin is caused by low data quality.
- #11 The HBV model with the glacier retreat model is further used to project water resources for the Chamkhar Chhu and Beas basins. The further climate is generated by two Global Climate Models with assumed carbon emissions. Their results are at spatial resolutions of several hundred kilometres, so they are downscaled by the two Regional Climate Models to a finer resolution of fifty kilometres. The precipitation and temperature are further downscaled and bias corrected to the observation sites. The comparison between the model results and observations in the historical period shows that the bias correction significantly reduces the error of RCMs.
- #12 Available water resources are defined as the water that can be consumed by human without causing environmental problems. It is estimated by excluding the environmental water requirement. In this figure, the x axis is the period from 2011 to 2050. Each point is the mean of five years water resources per capita. As we can see, the available water resources are significantly decreasing. To separate the effects of climate change and population, assuming that the population does not grow, the green line is the mean of the projected water resources. Population growth is responsible for 40 percent of the decrease. The uncertainties can be caused by the used models and the estimation of population. The shade represents the range by 20 percent error in population estimation. As we can see that, the population data cause more uncertainty than the models.