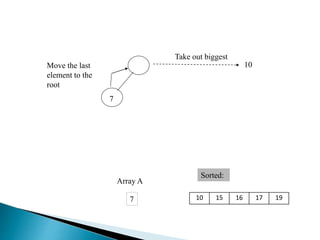
Heap is a complete binary tree represented as an array. There are two main types: min heap and max heap. A max heap has the largest element at the root and each parent is greater than or equal to its children. Heap sort uses the heap property to sort an array in O(n log n) time. It first builds a max heap from the array. Then it repeatedly removes the maximum element from the heap, adding it to the sorted portion of the array.

1. Design And Analysis Algorithm

2. Heap is a “complete” binary tree, usually
represented as an array.
Types:
 Min Heap (largest element at root)
A[parent(i)]≥A[i]
 Max Heap
A[parent(i)]≤A[i]

3. “The root is the
maximum element of the
heap!”
Example of Max
Heapify

4. 15
19 10
17 16
15
19 16
177 10
15 19 10 7 17 16
19
15 16
17 10
19
17
157 10
swap
16
7
7

5. 17 16
157 10
Move the last element
to the root
19
Sorted:Array A
17 16 7 15 10

6. 17 16
157
10
19
Array A
Sorted:
swap
HEAPIFY()
10 17 16 7 15

7. 10
157
16
19
Array A
Sorted:
17
17 10 16 7 15

8. 10
17
157
16
1917
Array A
Sorted:
Take out biggest
Move the last element
to the root
10 16 7 15

9. 10
15
7
16
1917
Array A
Sorted:
15 10 16 7

10. 10
15
7
16
1917
Array A
Sorted:
HEAPIFY()
swap
15 10 16 7

11. 16
10
7
15
1917
Array A
Sorted:
16 10 15 7

12. 16
10
7
15
1916 17
Array A
Sorted:
Take out biggest
Move the last
element to the
root
10 15 7

13. 10
7
15
1916 17
Array A
Sorted:
swap
7 10 15

14. 10 7
15
1916 17
Array A
Sorted:
71015

15. 10 7
15
1916 1710 15
Array A
Sorted:
Move the last
element to the
root
Take out biggest
77

16. 10
7
107
Array A
Sorted:
HEAPIFY()
swap
15 16 17 19

17. 7
10
Array A
Sorted:
107 15 16 17 19

18. 10
7
7
Array A
Sorted:
Move the last
element to the
root
Take out biggest
10 15 16 17 19

19. 7
Array A Sorted:
Take out biggest

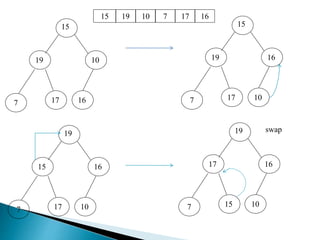
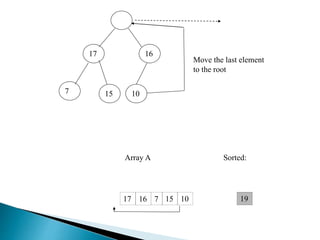
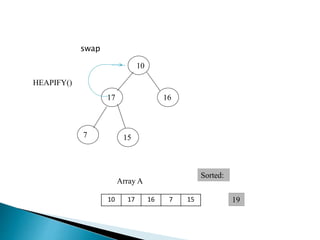
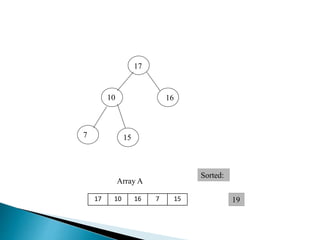
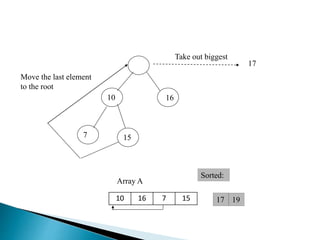
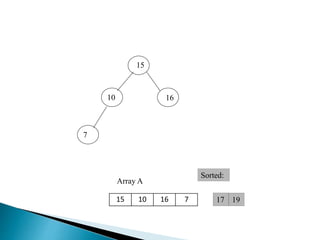
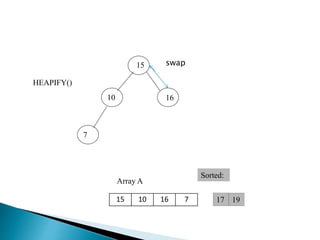
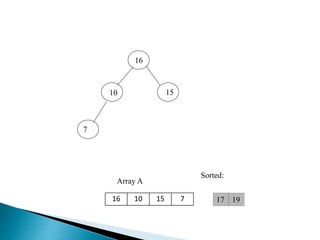
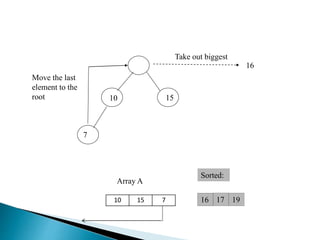
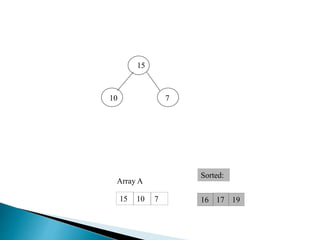
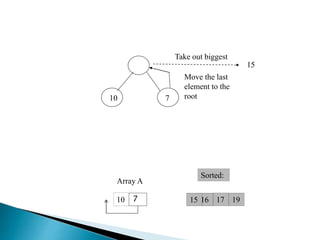
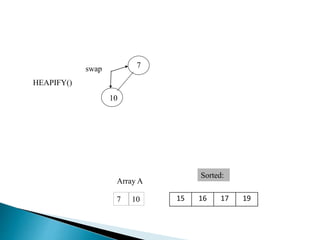
20.  BUILD‐MAX‐HEAP(A)
 1. heap‐size[A] ← length[A]
 2. for i ← ⌊length[A]/2⌋ downto 1
 3. do MAX‐HEAPIFY(A,i)

21.  Heap sort has time complexity O(n log n). The reason is that the
height of a complete binary tree is log(n).
 To fully heapify an element whose sub trees are already max-heaps,
we need to keep comparing the element with its left and right
children and pushing it downwards until it reaches a point where
both its children are smaller than it.
 In worst case, we need to move an element from root to leaf node
making a multiple of log(n) comparisons and swaps. During the
build max heap stage, we do that for n/2 elements so the worst case
complexity of build heap step is n/2*log(n)~n log n.