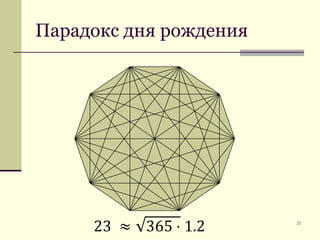
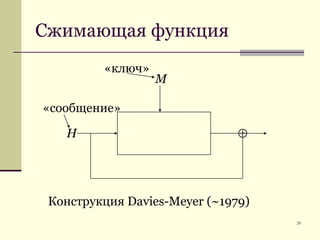
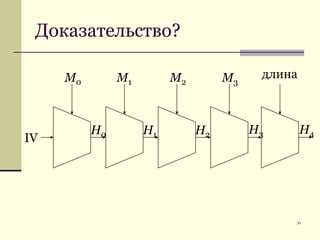
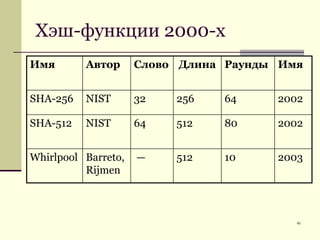
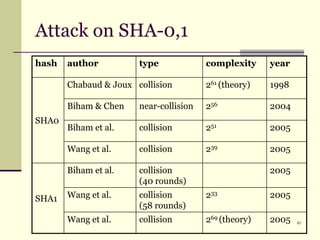
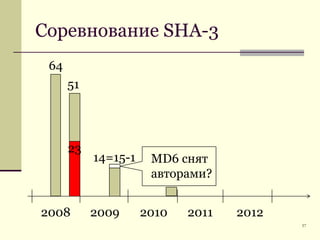
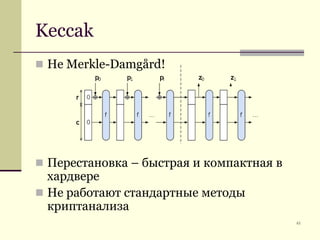
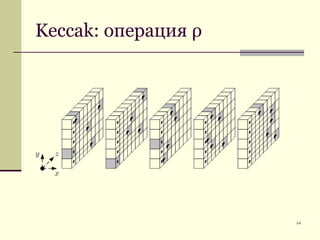
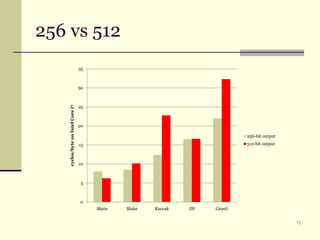
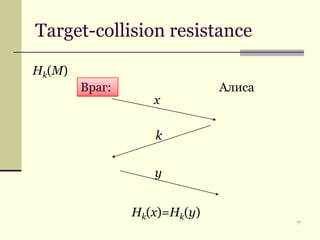
Документ обсуждает криптографические хэш-функции, их конструкции, применения и атаки на них. Основное внимание уделяется стандарту SHA-3 и различным методам, таким как схемы Davies-Meyer и Merkle-Damgård. В документе также представлены примеры применения хэш-функций, включая цифровые подписи и SSL/TLS.

1. 1Криптографическиехэш-функцииИлья МироновЕкатеринбург16-17 апреля, 2011

2. О докладчике1993-99 мат-мех СПбГУ1999-2003 Ph.D., Стэнфорд, СШААнализ RC4 как тасование колоды карт2003- Microsoft Research, Silicon Valleyкриптографияprivacy2

3. Microsoft ResearchБолее 800 человекАктивная программа стажеров!3

4. Почему хэш-функции?Один из основных примитивовОбманчивая простотаУвлекательная теорияМеждународный конкурс!4

5. ПланОпределение, примененияКонструкция:Davies-MeyerMerkle-DamgårdОбщие атакидемонстрацияКонкретные хэш-функцииСоревнование SHA-3Заключение5

6. ПланОпределение, примененияКонструкция:Davies-MeyerMerkle-DamgårdОбщие атакидемонстрацияКонкретные хэш-функцииСоревнование SHA-3Заключение6

7. Мир хэш-функций7

8. Мир хэш-функций8Стандарт SHA-3

9. 9Что такое хэш-функция?H: {0,1}*->{0,1}nсообщениехэшHxM

10. 10Что такое хэш-функция?Hk: {0,1}*->{0,1}nk— ключ или индекссообщениехэшHxM

11. Что такое криптографическая хэш-функция?Устойчивость к нахождению:прообразаколлизиивторого прообразаM????=x?x?x11

12. Применение: Таблицы паролей12АлисаБобпарольH(пароль) ?=H(пароль1)пароль ?= пароль1принять или отказать12

13. Требование к безопасности?13Дано:x=H(пароль)Найти: любую строку M, удовлетворяющуюH(M) = xH — устойчива к нахождению прообраза (односторонняя функция)

14. Применение:Цифровые подписи14Схема RSAпараметры: N = pq,ed= 1 mod φ(N)подпись:C=Mdmod Nпроверка:Ce=M mod Nподпись:C=H(M)dmod Nпроверка:Ce=H(M)mod NПроблемы:длинное M

15. C является подписью для любого M + kNПрименение: SSL/TLS15АлисаСерверhttp://amazon.comэтот ключ принадлежитAmazon.com+подписьоткрытый ключсертификат15

16. Применение: SSL/TLS16АлисаСерверhttp://amazon.comоткрытый ключсертификат16

17. Требования к безопасности?17Дано:C— подпись M, то естьC = H(M)d mod NНайти: строку M′, удовлетворяющуюH(M) = H(M′)H — устойчива к нахождению второго прообраза

18. Переговоры18переговорыАлисаБобдоговордоговор+подпись18

19. Переговоры19переговорыАлисаБобдоговор′договордоговор+подписьдоговор′+подпись19

20. Требования к безопасности?20Найти: любые две строки Mи M′, так чтоH(M) = H(M′)H — устойчива к нахождению коллизий

21. Стойкость идеальной хэш-функцииУстойчивость к нахождению:21прообразавторого прообразаколлизииM????=x?x?x2n2nвычислений2n/2

22. Парадокс дня рождения2223 ≈365⋅1.2

23. 23ТеорияКоллизииОбязательно существуютПарадокс дня рождения: 2n/2Второй прообраз 2nОдносторонность 2nDan Simon’98

24. ПланОпределение, примененияКонструкция:Davies-MeyerMerkle-DamgårdОбщие атакидемонстрацияКонкретные хэш-функцииСоревнование SHA-3Заключение24

25. 25КонструкцииДве основных компонентыСжимающая функцияИтератор

26. 26Сжимающая функция512 бит160 бит

27. 27Сжимающая функция512 бит160 бит

28. 28Сжимающая функция«ключ»M«сообщение»HКонструкция Davies-Meyer (~1979)

29. 29ИтераторM0M1M2M3H0H1H2H3IVКонструкция Merkle-Damgård (1989)

30. 30Доказательство?длинаM0M1M2M3H3H4H0H1H2IV

31. 31Обзор конструкцииMH(M)

32. 32Обзор конструкциидлинаM0M1M2M3H3H4H0H1H2IV

33. 33MОбзор конструкции

34. 34Обзор конструкцииa1a2a3a48b1b2b3b48…c1c2c3c48d1d2d3d48

35. 35IVЧерный ящикНеMH(M)

36. 36АутентификацияkM1M2M3H0H1H2H3IVMAC: Hk(M) = H(k || M)Hk(M || M3) = C(Hk(M), M3)

37. HMACMAC: Hk1,k2(M) = H(k2 || H(k1|| M))Доказательство основывается на устойчивости к коллизиям37

38. 38Каскадные хэш-функцииF(M) = G1(M)|| G2(M) – каскадная функция«ЕслиG1 иG2независимы, то для поиска коллизии дляFнеобходимо найти коллизии для обеих функций одновременно.Это требует произведения усилий, необходимых для атак на G1 иG2по отдельности.»Handbook of Applied Cryptography

39. 39Атака Жу (Joux)M0, N0M1, N1M2, N2M3, N3H0H1H2H3IVk 2n/2 усилия для нахождения 2k коллизий

40. 40Атака ЖуПроделав k·2n/2вычислений, находим 2kколлизий для G1Положив k = n/2, мы найдем среди них коллизиюM, Nдля G2G1(M) = G1(N) и G2(M) = G2(N)

41. 41«Отравленный блок»M0M3M1M2, N2H0H1H2H3IV

42. 42if (R1 == R1) then print(“Dr. Jekyll”) else print(“Mr. Hyde”)if (R2== R1) then print(“Dr. Jekyll”) else print(“Mr. Hyde”)Атакуем Postscript

43. ПланОпределение, примененияКонструкция:Davies-MeyerMerkle-DamgårdОбщие атакидемонстрацияКонкретные хэш-функцииСоревнование SHA-3Заключение43

44. Краткая история44SHA-2SHA-3256256SHA-0SHA-1160MD5512128MD451212819901995201020002005

45. 45Хэш-функции 90-х

46. 46Хэш-функции 2000-х

47. 47Attacks onMD4-MD5

48. 48Attacks onMD4-MD5

49. 49Attack onSHA-0,1

50. Развитие атак50Первое поколение атак на MD4,MD5, SHA-0,1:M1M21-3×64 байт

51. Развитие атак51Произвольный префикс:M1M21-3×64 байт

52. Sotirov et al.’0852Self-signedMD5 CollisionsRapidSSLuser1user2user3

53. Два сертификата53префиксыколлизияидентичныебиты

54. ПланОпределение, примененияКонструкция:Davies-MeyerMerkle-DamgårdОбщие атакидемонстрацияКонкретные хэш-функцииСоревнование SHA-3Заключение54

55. Соревнование SHA-3В 2005 году принято решение о выработке нового стандарта в рамках соревнованияМодель – стандарт AESФормальное объявление – 2 ноября 2007Начало соревнования: конец 2008 годаПервый раунд: 15 кандидатовВторой раунд: 5 кандидатовВыбор финалиста – 2012 год55

56. Соревнование SHA-3645114512008200920102011201256

57. Соревнование SHA-364512314=15-1MD6 снят авторами?52008200920102011201257

58. ФиналистыBLAKEGrøstlJHKeccakSkein58

59. BLAKEИнтересная внутренняя структураНепрозрачный дизайн:много произвольно выбранных констант нет доказательств хорошая скорость59

60. GrøstlОснован на AES:может использовать AES-NI много статей, один из медленныхrebound attack60

61. KeccakНе Merkle-Damgård!Перестановка – быстрая и компактная в хардвереНе работают стандартные методы криптанализа 61

62. Keccak“Трехмерный AES”62

63. Keccak: операция θ63

64. Keccak: операция ρ64

65. Keccak: операция π65

66. Keccak: операция χ66

67. JHНе Merkle-Damgård4-битовые S-BoxОтносительно малоизучен67

68. SkeinСамый простойТрадиционные компоненты:Davies-MeyerMerkle-DamgårdТри операции: +, ≪, ⊕ 68

69. Структура8- битовый S-Box: Grøstl4-битовый S-Box: Keccak, JH+, ≪, ⊕: BLAKE, Skein 69

70. Скорость на Intel Core i770Источник: http://bench.cr.yp.to/web-impl/amd64-ellprecisio-crypto_hash.html

71. 256 vs 51271

72. Производительность на хадвере72

73. ПланОпределение, примененияКонструкция:Davies-MeyerMerkle-DamgårdОбщие атакидемонстрацияКонкретные хэш-функцииСоревнование SHA-3Заключение73

74. Что дальше?Не использовать MD4, MD5, SHA-1Готовиться к новому стандартуРежимы использования хэш-функций:рандомизацияпереход с HMAC на другие виды MAC’ов 74

75. Анонс: Лекции завтраЛекция 1:Поиск коллизийбез использования памятипараллельныйдля инкрементальных хэш-функцийРазмен память/времяЛекция 2:Модель случайного оракулаНеразличимость конструкций75

76. 76АутентификацияUMAC John Black, ShaiHalevi, Hugo Krawczyk, Ted Krovetz, and Phillip Rogaway, 1999на длинных сообщения ~1.5 такта/байт

77. 77Target-collision resistanceHk(M)Враг: АлисаxkyHk(x)=Hk(y)

78. 78TCR хэшHk(M) – TCRДля подписи M:Генерируем случайное kПодписываем k || Hk(M)Атака?Найти M′,так чтоk || Hk(M) = k || Hk(M′)