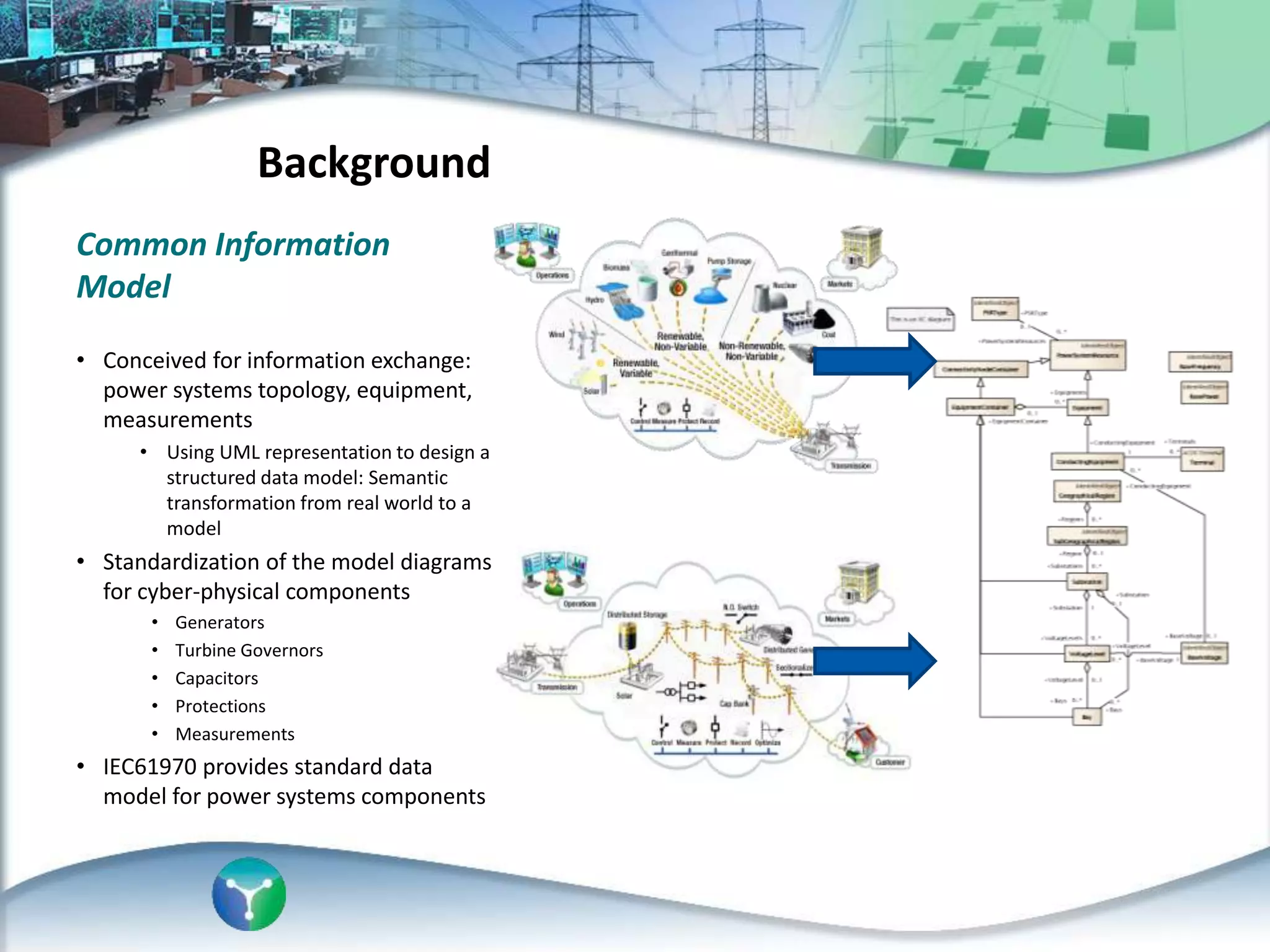
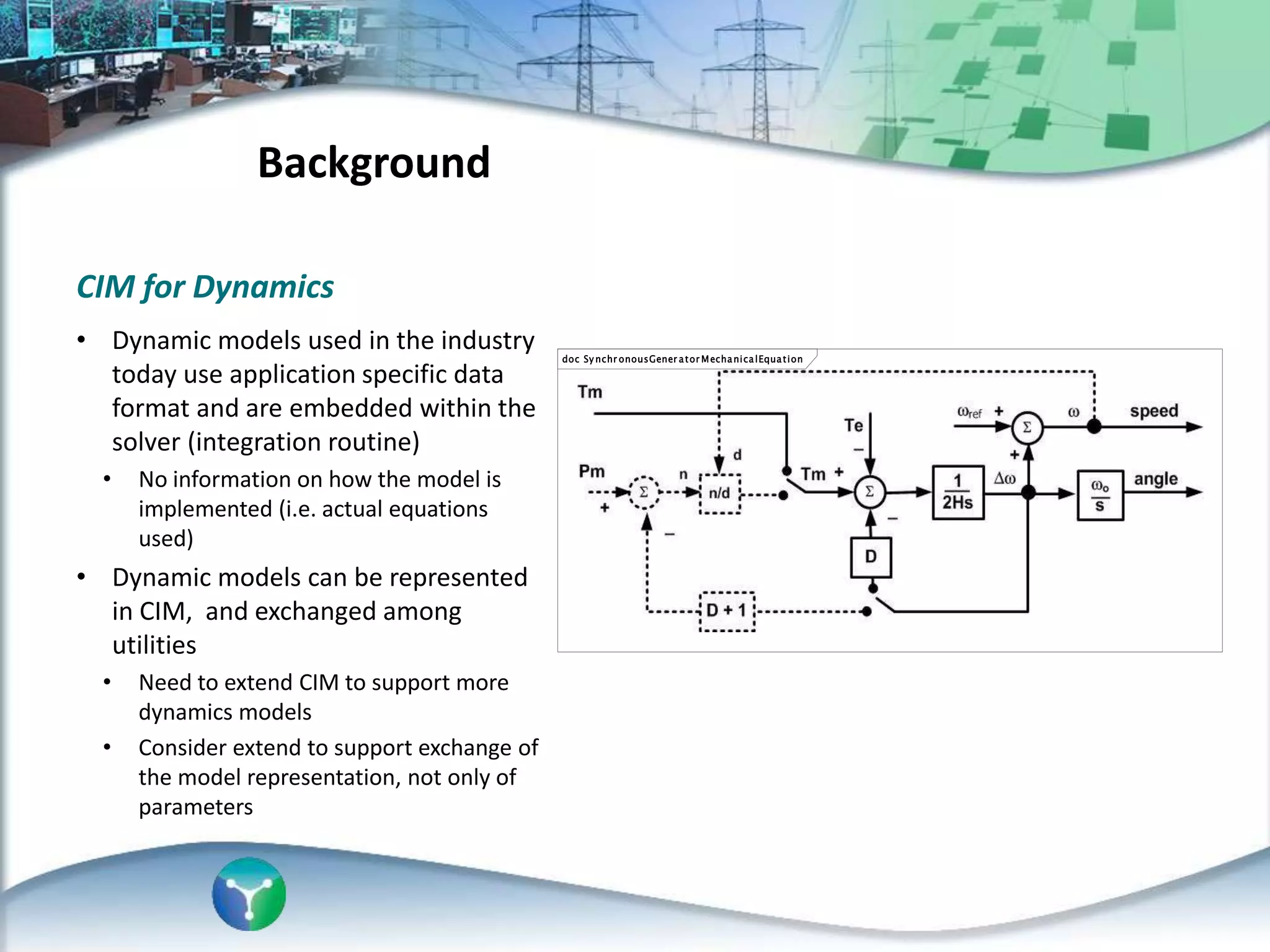
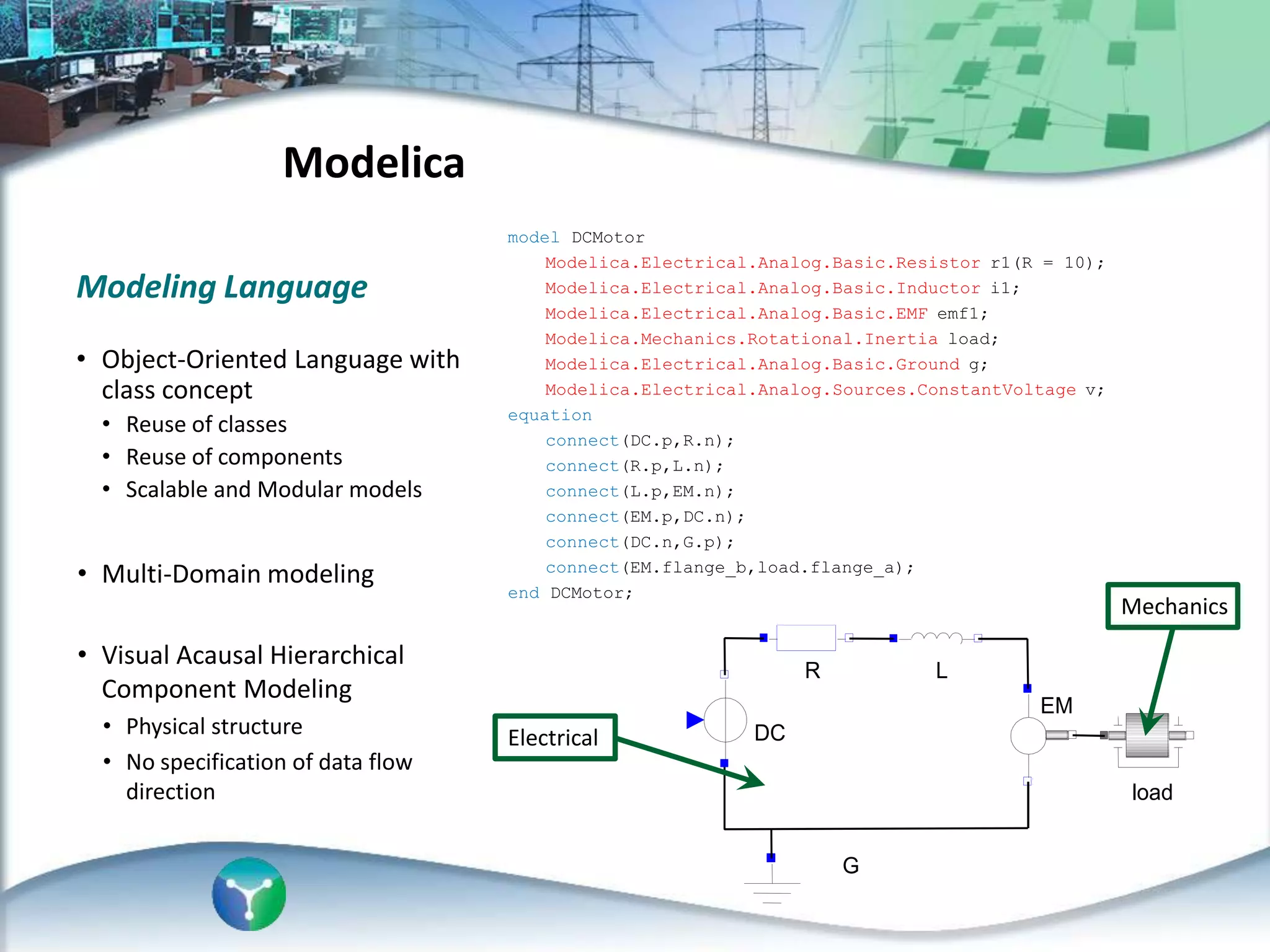
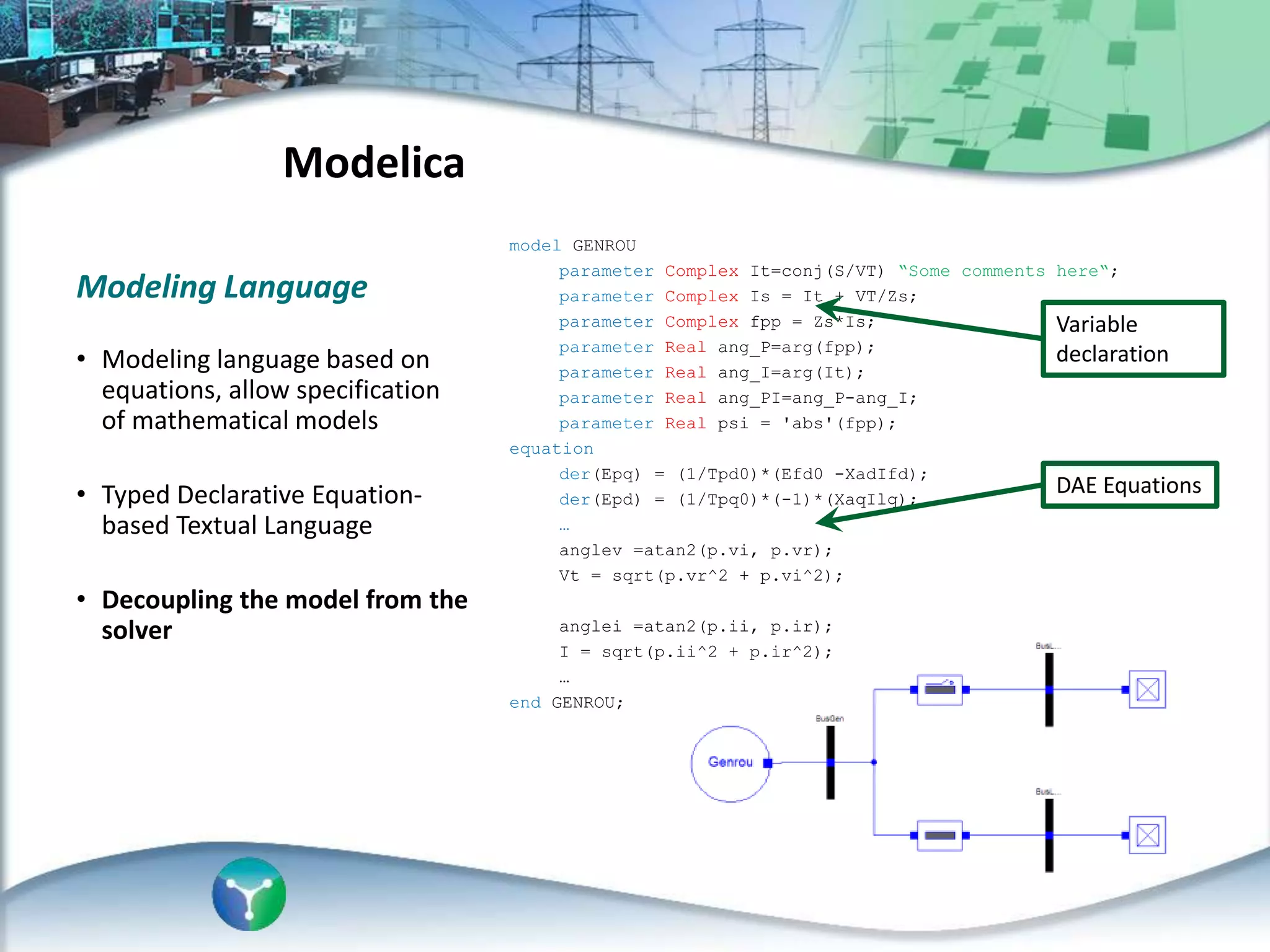
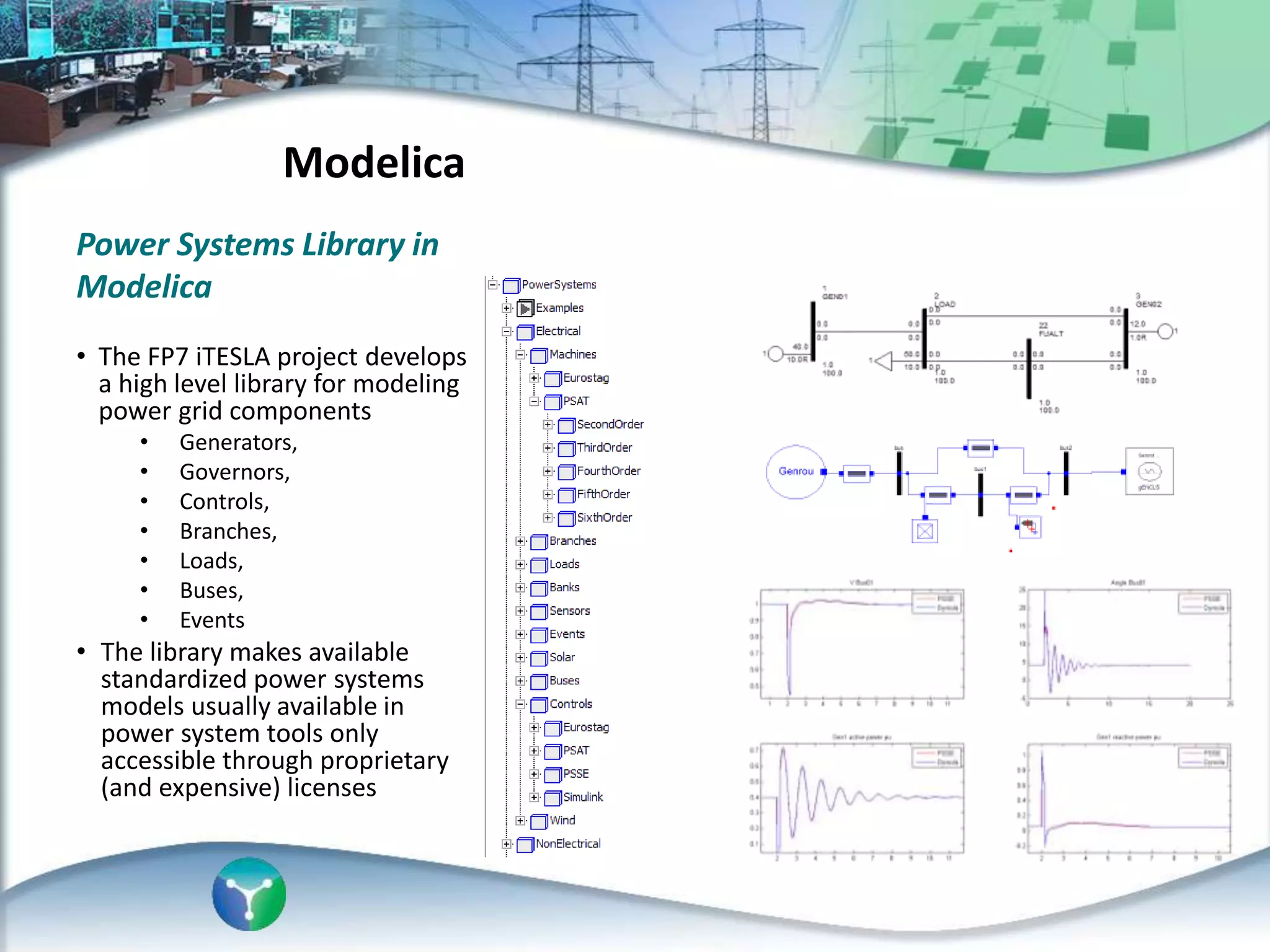
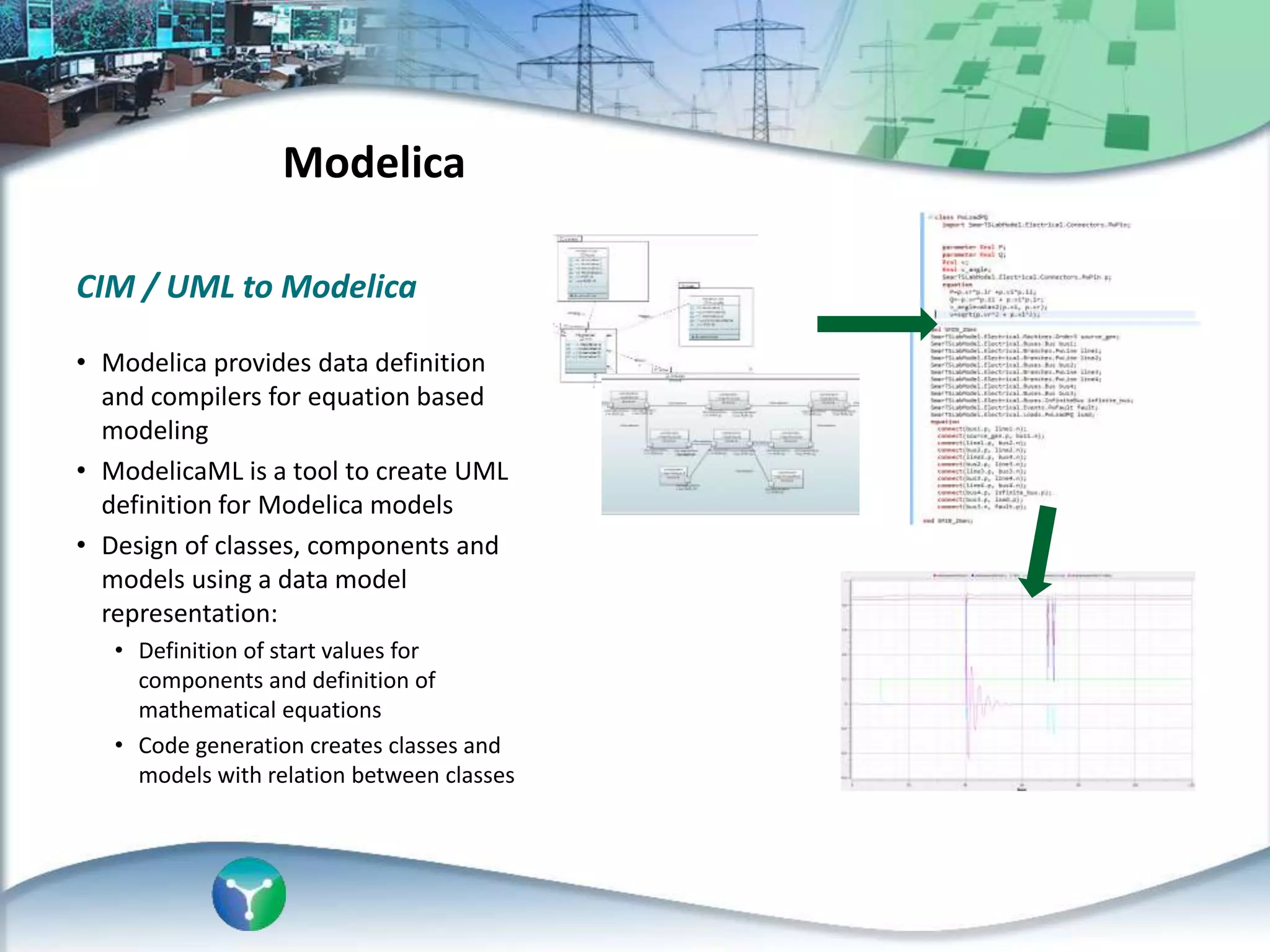
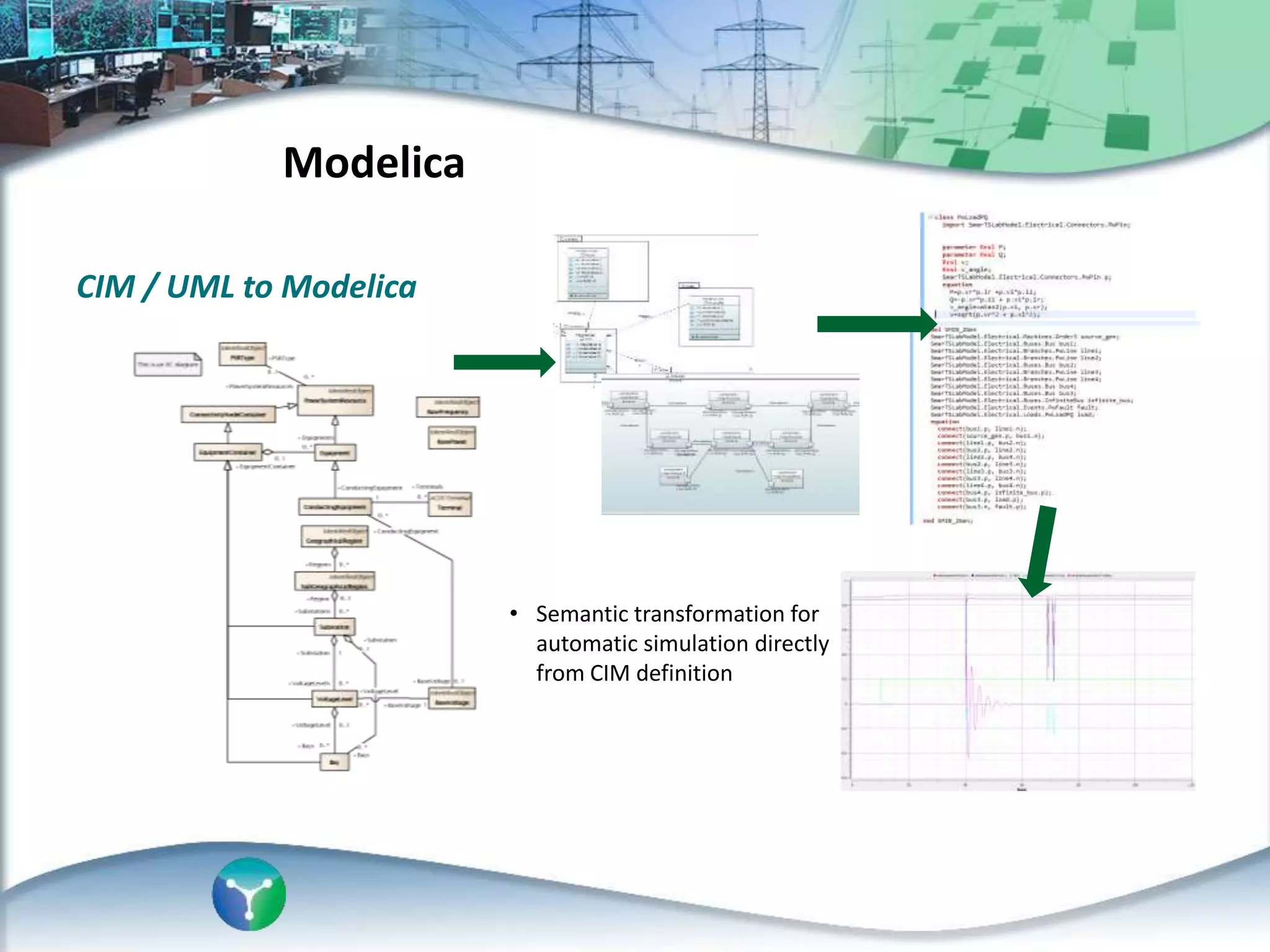
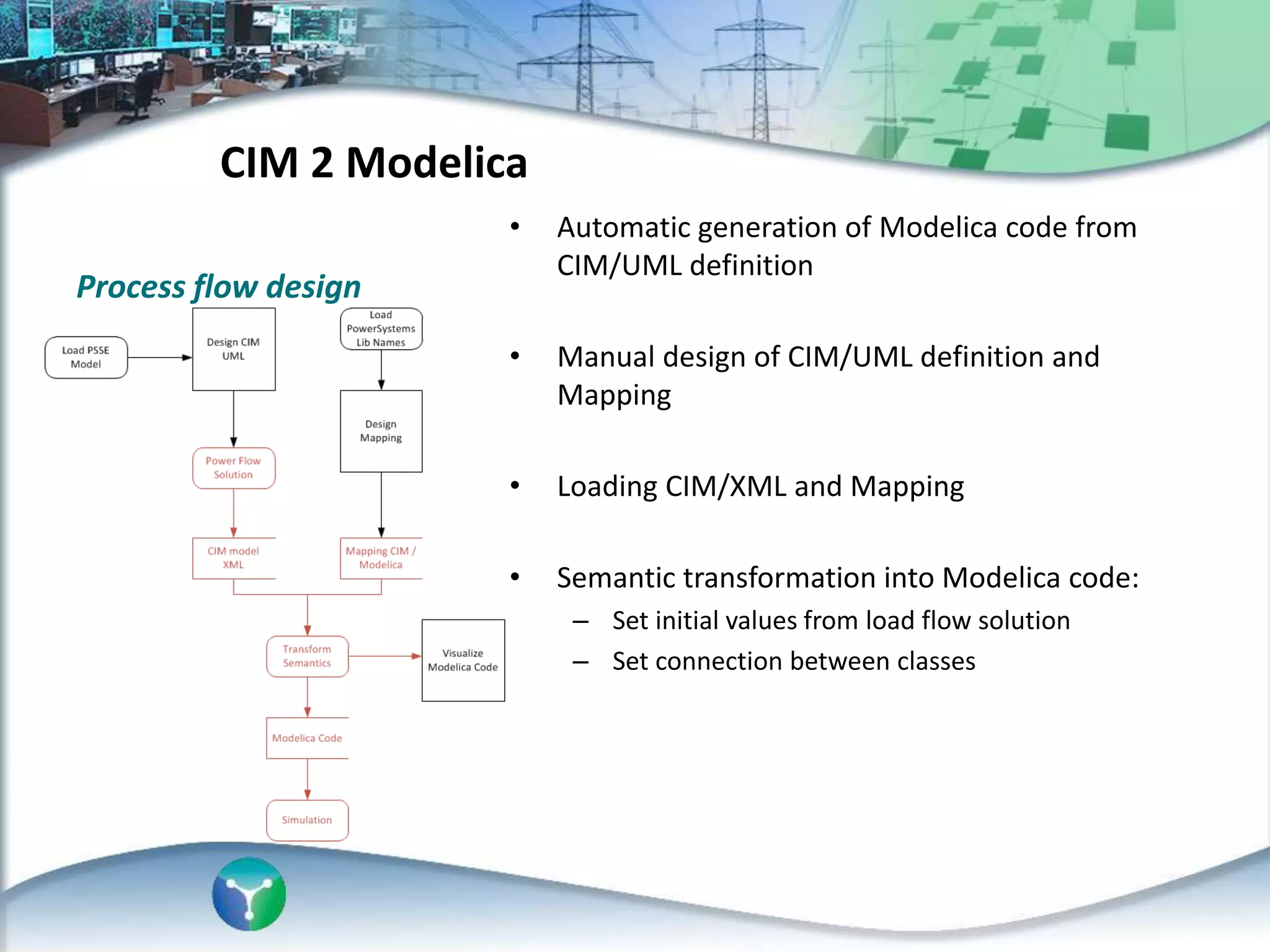
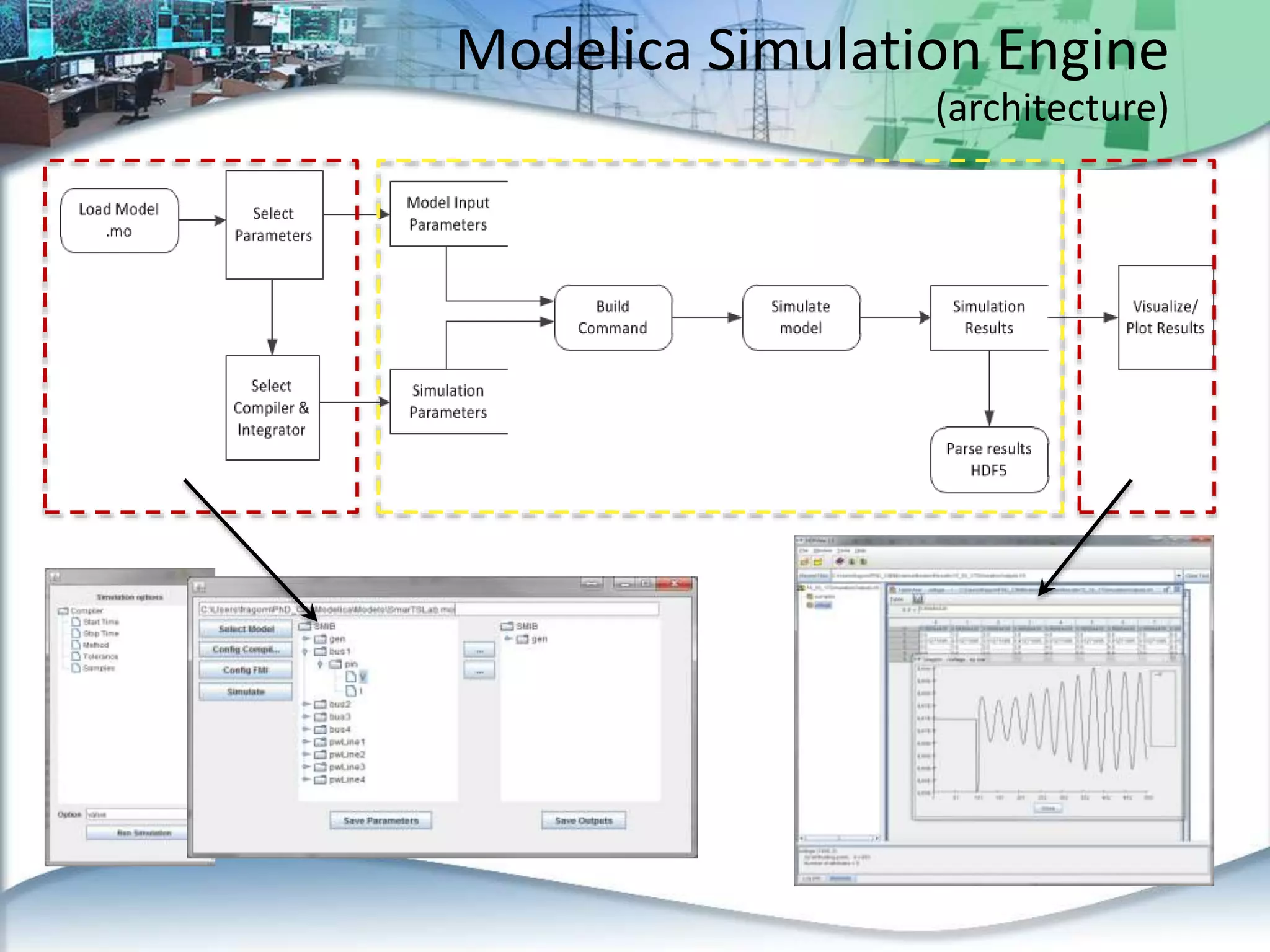
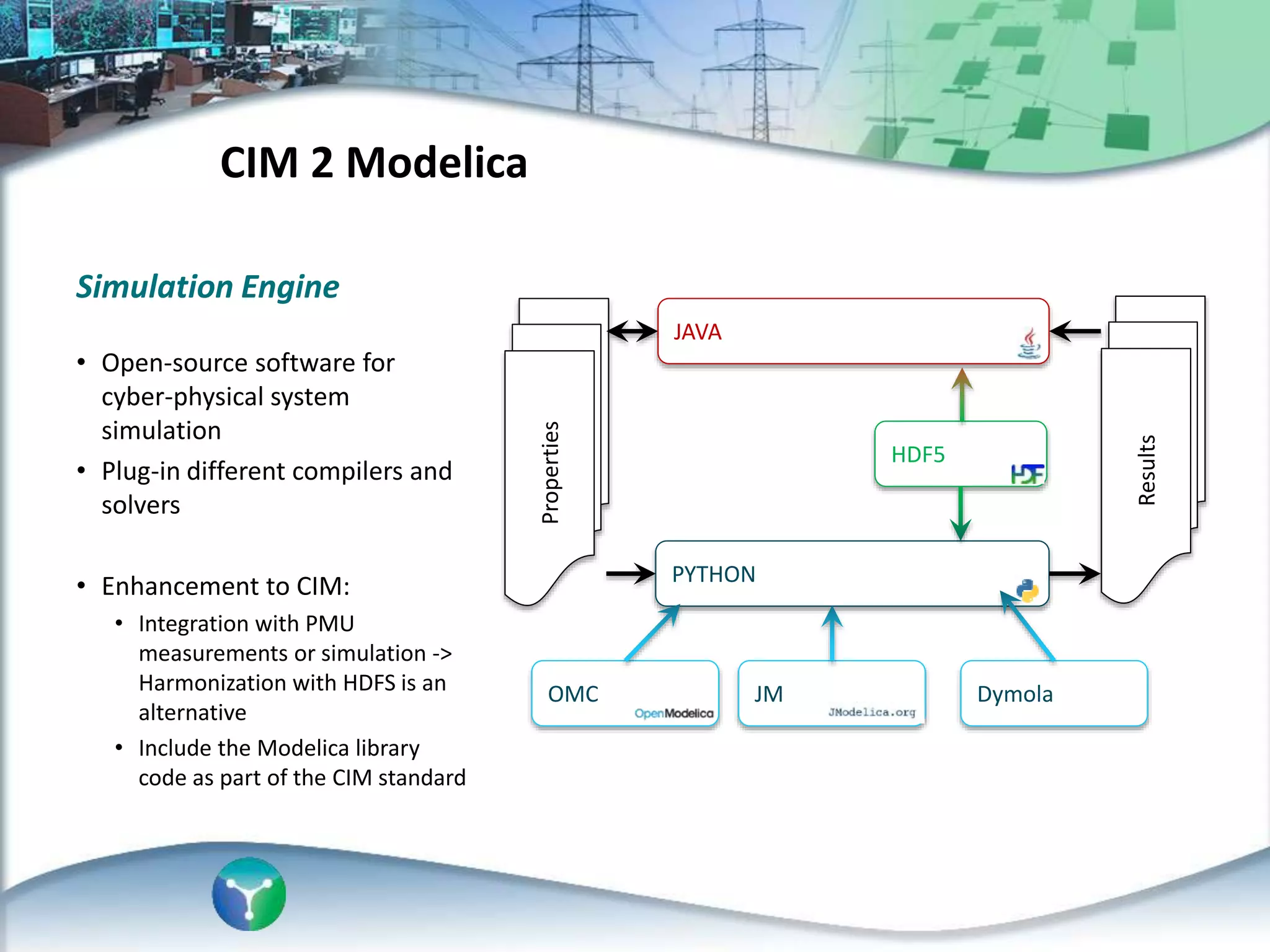
This document discusses an automated approach to generating Modelica models from CIM (Common Information Model) definitions for power system simulation. CIM provides a standard format for power system data, while Modelica is a modeling language suitable for complex physical systems. The proposed process involves semantically transforming CIM/UML definitions into Modelica code based on a defined mapping. This allows running time-domain simulations using standard power system models directly from utility data in CIM format. The resulting Modelica simulation engine could integrate real measurements to enable validation of generated models.

1. CIM 2 Modelica Factory
Automated Equation-Based Cyber-Physical Power System Modelica
Model Generation and Time-Domain Simulation from CIM
Francisco Gomez1, Prof. Luigi Vanfretti1,2, and Svein
H. Olsen2
luigiv@kth.se , fragom@kth.se
Electric Power Systems Dept.
KTH
Stockholm, Sweden
Luigi.Vanfretti@statnett.no
svein.harald.olsen@statnett.no
Research and Development Division
Statnett SF
Oslo, Norway

2. Overview
Acknowledgments
• This work has been funded in part by the
EU funded FP7 iTesla project:
http://www.itesla-project.eu/ and Statnett
SF, the Norwegian power system operator.
• Work related to the iTesla Modelica power
systems library presented here is a result of
the collaboration between RTE (France),
AIA (Spain) and KTH (Sweden) within the EU
funded FP7 iTesla project:
http://www.itesla-project.eu/
• Special thanks for ‘special training’ and
support from
• Prof. Fritzson and his team at Linköping University
• Prof. Berhard Bachmann and Lennart Ochel, FH
Bielefeld
• Background & Motivation
– Modelica
– CIM
– CIM for Dynamics
• Modelica
– Language Description
– MetaModelica
– CIM/UML to Modelica
• CIM 2 Modelica
– Concept Design
– Mapping
– Simulation Engine

3. Research
• Development of software architecture
supporting transformation from CIM,
implementing tools for either translating
from CIM to Modelica models
• Development of models of cyber-physical
power systems components,
communication network components, and
other components from other domains
Application
• iTESLA: Innovative Tools for Electrical
System Security within Large Areas
• CIM provides standard format for power
systems data
• Use of data from TSO
– Description of data equipment, power systems
topology and measurements for model validation
Motivation

4. Modelica
• Modelica is a non-proprietary, object-
oriented, equation based language to
conveniently model complex physical
systems
• Suitable modeling language for
standardization and exchange of
models
• Modelica tools, commercial and free of
charge
• Electric power steering and
controller model
[1] Andreas Deuring, Johannes
Gerl, Harald Wilhelm
“Multi-Domain Vehicle Dynamics
Simulation in Dymola”,
Modelica Conference, Dresden,
2011
• Thermodinamic Network
of the ICE model
[2] L. Morawietz, S. Risse, H.
Zellbeck, H. Reuss, T. Christ
“Modeling an automotive power
train and electrical power supply
for HiL applications using
Modelica”,
Modelica Conference, Hamburg,
2005
TU Dresden, University of
Stuttgart, BMW Group,
Germany.
Background

5. Common Information
Model
• Conceived for information exchange:
power systems topology, equipment,
measurements
• Using UML representation to design a
structured data model: Semantic
transformation from real world to a
model
• Standardization of the model diagrams
for cyber-physical components
• Generators
• Turbine Governors
• Capacitors
• Protections
• Measurements
• IEC61970 provides standard data
model for power systems components
Background

6. CIM for Dynamics
• Dynamic models used in the industry
today use application specific data
format and are embedded within the
solver (integration routine)
• No information on how the model is
implemented (i.e. actual equations
used)
• Dynamic models can be represented
in CIM, and exchanged among
utilities
• Need to extend CIM to support more
dynamics models
• Consider extend to support exchange of
the model representation, not only of
parameters
Background
doc Sy nchr onousGener ator MechanicalEquation

7. Extension for CIM
Dynamics
• Automatic model transformation
from CIM to a well defined
(equation based) language
• Information exchange,
parameters and equations with
CIM and Modelica
• The benefit / role of CIM:
• Modelling of the network are
done separate from the analytic
• Existing Steady-State Solver
Engine (SSSE) can be used to
initialize the transient study
Background
model gensal
…
parameter Real wbase = 2 * pi * 50 "system base speed";
parameter Complex Epqp = fpp + a * It;
parameter Real delta0 = arg(Epqp);
parameter Real Pm0 = p0 + (id0 * id0 + iq0 * iq0) * Ra;
Real delta "rotor angle";
Real w "machine speed deviation, p.u.";
…
initial equation
delta = delta0;
w = 0;
equation
…
der(w) = ((Pm0 - D * w) / (w + 1) - Te) / (2 * H);
der(delta) = wbase * w;
end gensal;

8. Overview
• Background & Motivation
– Modelica
– CIM
– CIM for Dynamics
• Modelica
– Language Description
– MetaModelica
– CIM/UML to Modelica
• CIM 2 Modelica
– Concept Design
– Mapping
– Simulation Engine

9. Modeling Language
• Object-Oriented Language with
class concept
• Reuse of classes
• Reuse of components
• Scalable and Modular models
• Multi-Domain modeling
• Visual Acausal Hierarchical
Component Modeling
• Physical structure
• No specification of data flow
direction load
EM
DC
G
R L
Electrical
Mechanics
model DCMotor
Modelica.Electrical.Analog.Basic.Resistor r1(R = 10);
Modelica.Electrical.Analog.Basic.Inductor i1;
Modelica.Electrical.Analog.Basic.EMF emf1;
Modelica.Mechanics.Rotational.Inertia load;
Modelica.Electrical.Analog.Basic.Ground g;
Modelica.Electrical.Analog.Sources.ConstantVoltage v;
equation
connect(DC.p,R.n);
connect(R.p,L.n);
connect(L.p,EM.n);
connect(EM.p,DC.n);
connect(DC.n,G.p);
connect(EM.flange_b,load.flange_a);
end DCMotor;
Modelica

10. Modeling Language
• Modeling language based on
equations, allow specification
of mathematical models
• Typed Declarative Equation-
based Textual Language
• Decoupling the model from the
solver
model GENROU
parameter Complex It=conj(S/VT) “Some comments here“;
parameter Complex Is = It + VT/Zs;
parameter Complex fpp = Zs*Is;
parameter Real ang_P=arg(fpp);
parameter Real ang_I=arg(It);
parameter Real ang_PI=ang_P-ang_I;
parameter Real psi = 'abs'(fpp);
equation
der(Epq) = (1/Tpd0)*(Efd0 -XadIfd);
der(Epd) = (1/Tpq0)*(-1)*(XaqIlq);
…
anglev =atan2(p.vi, p.vr);
Vt = sqrt(p.vr^2 + p.vi^2);
anglei =atan2(p.ii, p.ir);
I = sqrt(p.ii^2 + p.ir^2);
…
end GENROU;
Variable
declaration
DAE Equations
Modelica

11. Power Systems Library in
Modelica
• The FP7 iTESLA project develops
a high level library for modeling
power grid components
• Generators,
• Governors,
• Controls,
• Branches,
• Loads,
• Buses,
• Events
• The library makes available
standardized power systems
models usually available in
power system tools only
accessible through proprietary
(and expensive) licenses
Modelica

12. CIM / UML to Modelica
• Modelica provides data definition
and compilers for equation based
modeling
• ModelicaML is a tool to create UML
definition for Modelica models
• Design of classes, components and
models using a data model
representation:
• Definition of start values for
components and definition of
mathematical equations
• Code generation creates classes and
models with relation between classes
Modelica

13. CIM / UML to Modelica
• Semantic transformation for
automatic simulation directly
from CIM definition
Modelica

14. • Background & Motivation
– Modelica
– CIM
– CIM for Dynamics
• Modelica
– Language Description
– MetaModelica
– CIM/UML to Modelica
• CIM 2 Modelica
– Concept Design
– Mapping
– Simulation Engine
Overview

15. Process flow design
• Automatic generation of Modelica code from
CIM/UML definition
• Manual design of CIM/UML definition and
Mapping
• Loading CIM/XML and Mapping
• Semantic transformation into Modelica code:
– Set initial values from load flow solution
– Set connection between classes
CIM 2 Modelica

16. CIM 2 Modelica Mapping
• Relation between CIM classes
and Power system library classes
• CIM Attributes and values ->
Modelica Variables and starting
values
• CIM relations between classes ->
Modelica connection between
components
or
• CIM relations between classes ->
Use of Modelica classes as objects
CIM 2 Modelica

17. Modelica Simulation Engine
(architecture)

18. Simulation Engine
• Open-source software for
cyber-physical system
simulation
• Plug-in different compilers and
solvers
• Enhancement to CIM:
• Integration with PMU
measurements or simulation ->
Harmonization with HDFS is an
alternative
• Include the Modelica library
code as part of the CIM standard
CIM 2 Modelica
Properties
Results
HDF5
JMOMC
PYTHON
JAVA
Dymola

19. Thank you! Questions?
luigiv@kth.se , fragom@kth.se
Electric Power Systems Dept.
KTH
Stockholm, Sweden
Luigi.Vanfretti@statnett.no
svein.harald.olsen@statnett.no
Research and Development Division
Statnett SF
Oslo, Norway