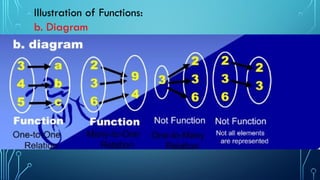
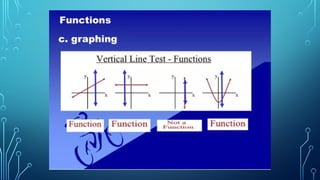
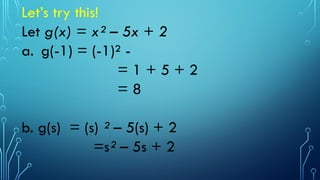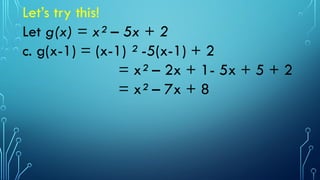The document provides an overview of functions in mathematics, defining them as relations where each input corresponds to exactly one output. It includes examples of functions, activities for determining domain and range, and illustrates the vertical line test to verify if a relation is a function. Additionally, it presents specific exercises for evaluating functions and applying mathematical principles.

1. GENERAL MATHEMATICS
ARNEL JR. A. MACUTAY, LPT

2. What we are about to learn..
a.Define functions and piece – wise functions
b.Determine whether a relation is a function or
not;
c.Represent real – life situations using functions
including piece – wise functions.

4. FUNCTIONS
Give another real – life situations involving functions.

5. Functions
A function is a relation in which each element of the
domain is paired with exactly one element of the range.
Another way of saying it is that there is only one output
(y) with each input (x).
Illustration of Functions:
a. set of ordered pair
b. mapping or arrow diagram
C. graphing

6. Functions
A function is a relation in which each element of the domain is paired
with exactly one element of the range. Another way of saying it is that
there is only one output (y) with each input (x).
Illustration of Functions:
a. set of ordered pair
1.{(3,2), (4,0), (5,1), (2,3)}
2.{(1,2), (0,3), (1,6), (5,4)}
3.{(3,4), (3,0), (3,1), (3,3)}
4.{(4,2), (3,2), (6,2), (5,2)}
1.Function
2.Not Function
3.Not Function
4.Function

7. Functions
A function is a relation in which each element of the domain is paired
with exactly one element of the range. Another way of saying it is that
there is only one output (y) with each input (x).
Illustration of Functions:
a. set of ordered pair (x, y)
x – First element DOMAIN
Independent Variable
y – Second element
RANGE
Dependent Variable

8. Activity #1
Find the domain and the range of the ff. set of ordered pair.
Do this in a ¼ sheet of paper.
1.{(1,2), (3,4), (5,6), (7,8)}
2.{(1,28), (2,29), (3,30), (4,31)}
3.{(3,a), (4,b), (5,c), (6,d), (7,e)}
4.{(2,9), (3,9), (6,4)}
5.{(3,2), (3,3), (3,4), (3,6)}
ANSWER!
1.x = (1,3,5,7) , y = (2,4,6,8)
2.x = (1,2,3,4) , y = (28,29,30,31)
3. x = (3,4,5,6,7) , y = (a,b,c,d,e,)
4. x = (2,3,6) , y = (9,4)
5. x = (3) , y = (2,3,4,6)

9. Illustration of Functions:
b. Diagram

10. To determine if y is a function of x, solve for y in terms of x.
x² – y = 4
x² – 4= y
Evaluate:
(1)² – 4= y, (2)² - 4 = y, (3)² - 4 = y,
(4)² - 4 = y
y = -3 y = 0 y = 5
y = 12
x = (1,2,3,4) y = (-
Example 1.1.1
Determine if the given equation represents y as a function of x.
a. x² – y = 4

11. Let’s try this!
Let g(x) = x² – 5x + 2
Find the following.
a.) g(-1)
b.) g(s)
c.) g(x - 1)

12. Let’s try this!
Let g(x) = x² – 5x + 2
a. g(-1) = (-1)² -
= 1 + 5 + 2
= 8
b. g(s) = (s) ² – 5(s) + 2
=s² – 5s + 2

13. Let’s try this!
Let g(x) = x² – 5x + 2
c. g(x-1) = (x-1) ² -5(x-1) + 2
= x² – 2x + 1- 5x + 5 + 2
= x² – 7x + 8

14. ACTIVITY #2
Evaluate the function at each specified value of the
independent variable and simplify.
1. g(x) = 5x -2
a. g(0)
b. g(-2)
c. g(x+1)
2. f(t) = -2t + 3
a. f(0)
b. f (1)
c. f( t + 1)

15. Exercise #1
Evaluate the function at each specified value of the
independent variable and simplify.
1. g(x) = 10x -5
a. g(10)
b. g(-4)
c. g(x+3)
2. f(s) = -2s + 20
a. f(-15)
b. f (10)
c. f( s -5)

16. PEMDAS(PARENTHESIS, EXPONENT, MULTIPLICATION,
DIVISION, ADDITION, SUBTRACTION)
1. (0)³ + 10 =
2. 15(5)²-50 =
3. 2(10)+30(5)-100 =
4. 125+9(15)+2(5)² - 2 =
5. 1(10)³+199+40(10)² - 8 =

17. Illustration of Functions:
c. Graphing
VERTICAL LINE TEST (PENCIL TEST)
If any vertical line passes through more than
one point of the graph, then that relation is
not a function.

19. THANKYOU
FOR YOUR
ACTIVE
LISTENING!