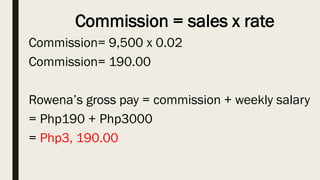
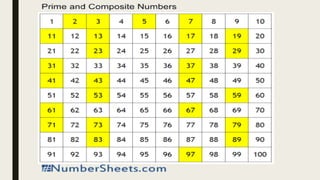
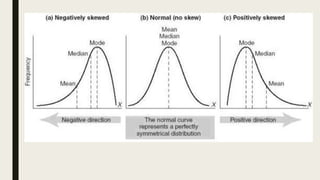
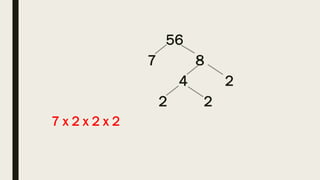
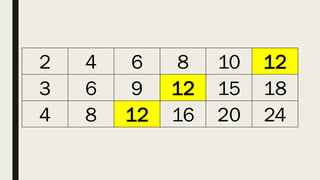
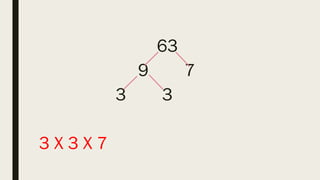
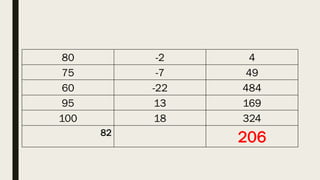
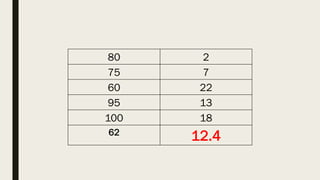
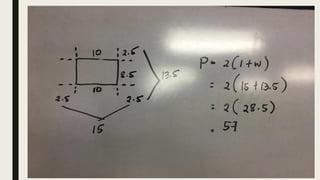
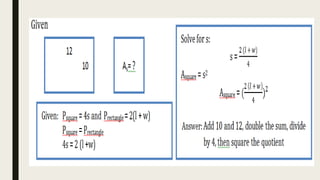
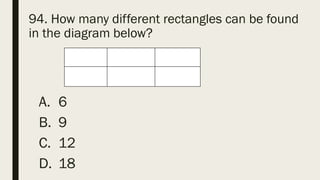
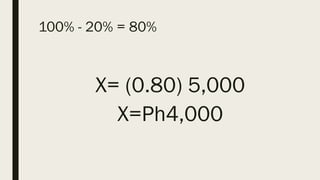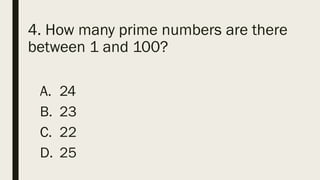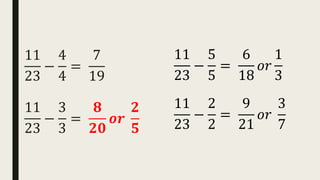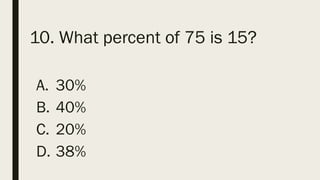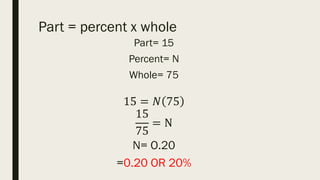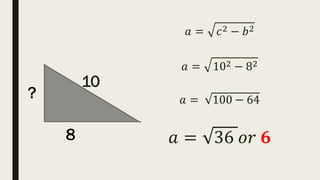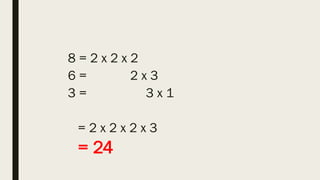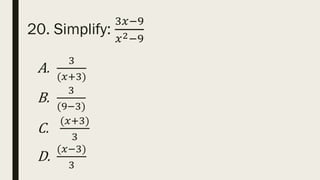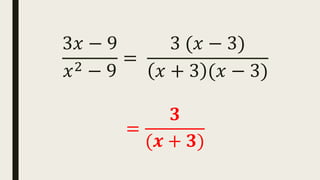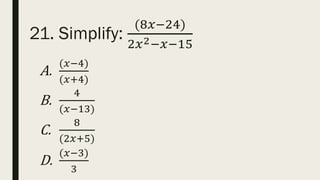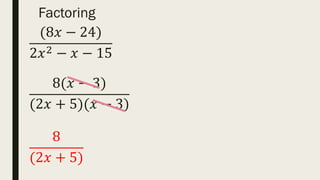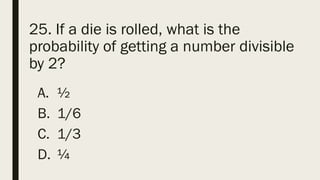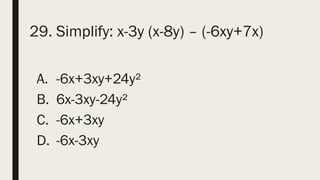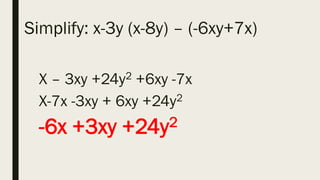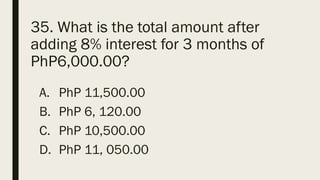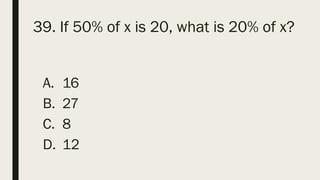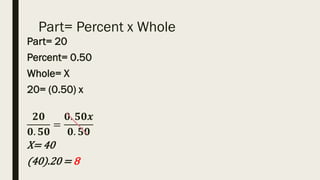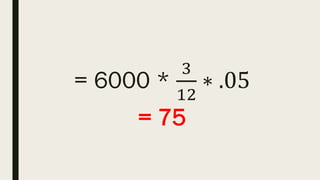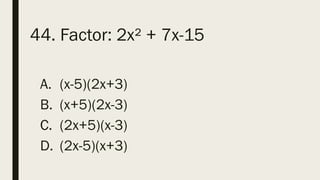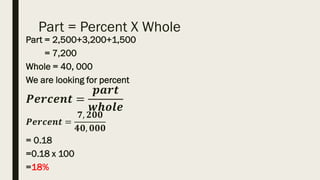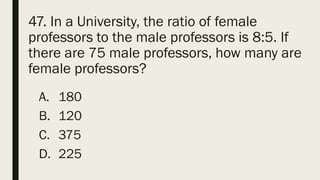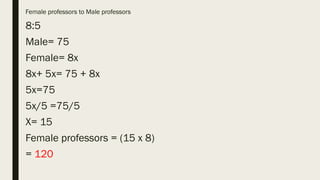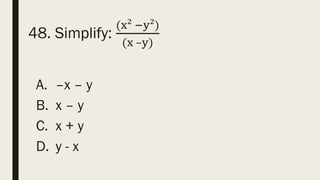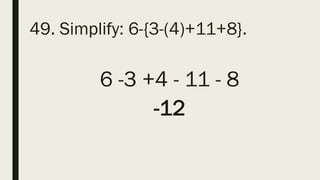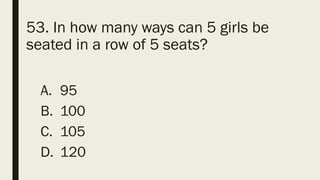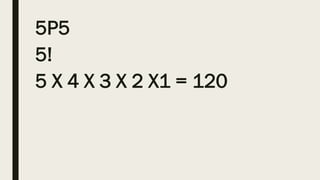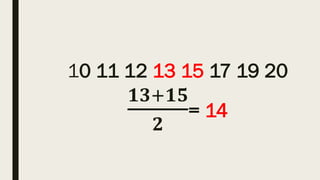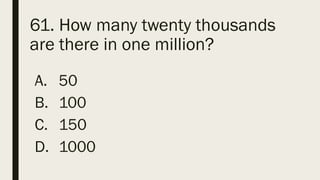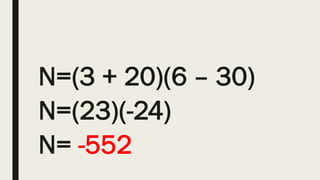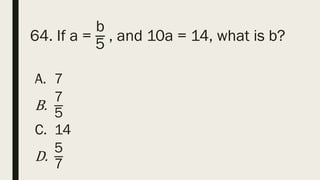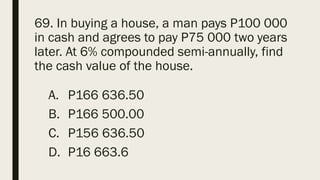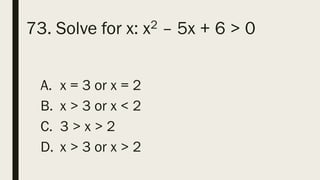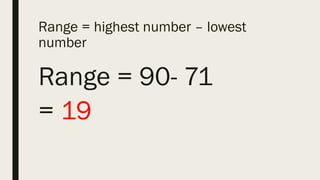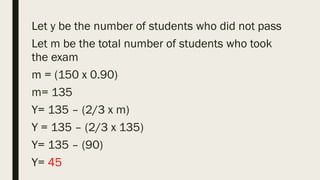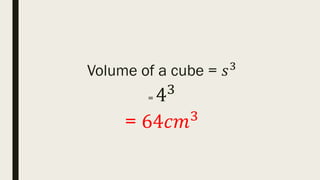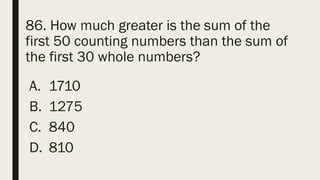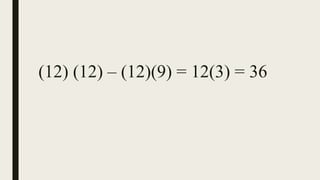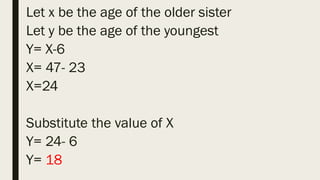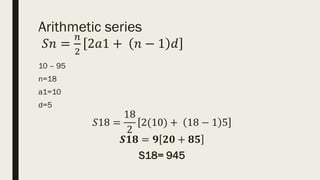This document contains a practice test with 36 multiple choice questions covering various math and science concepts. It provides instructions to take the test and wait for everyone to finish before answering. It also includes the questions, multiple choice answers, and solutions to each question. The document aims to help students prepare for an exam by providing a sample test for practice.