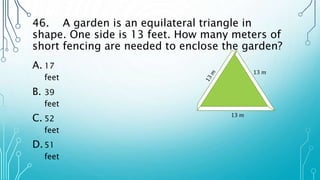
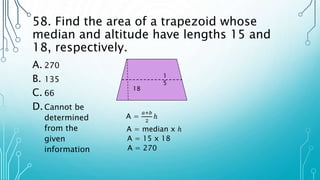
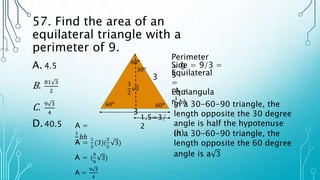
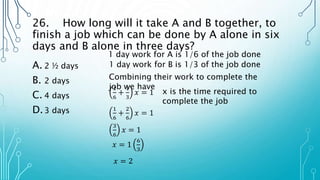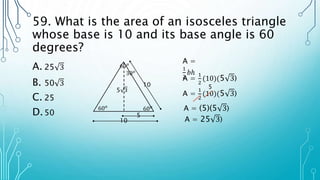The document contains multiple math word problems and their step-by-step solutions. It asks the reader to calculate various values like interest earned over time, the measures of angles, lengths and volumes of geometric shapes, rates of work, and more. The problems are explained clearly with diagrams and algebraic equations to show the rationalization for arriving at the answers.

1. CE 2 PRE-TEST 3
RATIONALIZATION

2. 4. Mr. Roy deposited P30,000.00 in the bank
at 5% simple interest per annum. How much is
his money in the bank after 5 years?
A. P37,500
B. P7,500
C. P75,000
D.P3,750
Interest = Principal x rate x time
I = P30,000.00 x 5% x 5
I = P30,000.00 x 0.05 x 5
I = 7,500.00
Amount in 5 years = 7,500.00 + Principal
Amount in 5 years = 7,500.00 + 30,000.00
Amount in 5 years = 37,500.00

3. 7. The sum of 2 numbers is 18. Four times the
smaller exceeds the larger by 7. Find the larger
number.
A. 13
B. 11
C. 7
D.5
Translate into
equations
x + y = 18 → equation
1
Let x be the smaller
number and
y the larger number
4x = y + 7 → equation
2
4x – y = 7 → transpose
y
Combine Eqn 1 and Eqn
2
x + y = 18
4x – y = 7
+
5x =
25
5 5
x = 5
Substitute to Eqn 1 or Eqn 2 to
find y
x + y = 18
5 + y = 18
y = 18 - 5
y = 13

4. 13. The sum of 2 numbers is 10. Five times the
smaller exceeds the larger by 2. Find the smaller
number.
A. 2
B. 3
C. 4
D.5
Translate into
equations
x + y = 10 → equation
1
Let x be the smaller
number and
y the larger number
5x = y + 2 → equation
2
5x – y = 2 → transpose
y
Combine Eqn 1 and Eqn
2
x + y = 10
5x – y = 2
+
6x =
12
6 6
x = 2

5. 16. Find the equation of the
line perpendicular to x + 2y -
6 = 0 and passing through the
origin.
A. 2x + y = 0
B. –2x – y =
0
C. 2x – y = 0
D.–x + 2y =
0
If m is the slope of a line, the
slope of a line perpendicular to it
is -1/m
(0, 0)
(x, y)
Transform the given equation to
slope-intercept form (y = mx +
b)
x + 2y - 6 =
0
2y = -x + 6
2 2
y = -x + 6
2 2
y = −
1
2
x + 3
y = mx + b
m = −
1
2
If m = -1/2 is the slope of the line,
the slope of a line perpendicular to
it is - (-2/1) = 2
Use the given point (0, 0) to
determine the y-intercept or b
y = mx + b 0 = 2(0) + b 0 = b
Substitute m and b to the new
equation
y = mx + b y = 2x + 0
-2x + y =
0
or 2x - y = 0

6. 17. What must be subtracted from 5𝑥3
−
2𝑥2
+ 3𝑥 − 5 to get 2𝑥3
− 8 + 5𝑥 − 2𝑥2
?
A. 3x3- 2x + 3
B. 3x3-4x2- 8x -
13
C. 7x3-4x2 + 8x -
13
D.7x3-4x2- 5x -
13
Align similar terms
5𝑥3 − 2𝑥2 + 3𝑥 − 5
2𝑥3 − 2𝑥2 + 5𝑥 − 8
3𝑥3 − 0𝑥2 − 2𝑥 +3
Subtract.
– + – +
+ Change the signs in the
subtrahend and proceed to
addition
3𝑥3 − 2𝑥 +3

7. 21. Calculate f(-2) if f(x) = 𝑥2
– 2x + 1.
A. 6
B. 7
C. 8
D. 9
Evaluating functions
f(x) = 𝑥2
– 2x + 1
f(-2) = (−2)2 – 2(-2) + 1
f(-2) = 4 + 4 + 1
f(-2) = 9

8. 19. If f(x) = 𝑥2
+ 2 and g(x) = 2/x, what is
the value of g o f(2)?
A. 3
B. 2
C. 1/3
D.1/2
Composition of functions g o f(x) =
g(f(x))
Simplify the inner function in g o f(x) =
g(f(x))
g o f(2) = g(f(2))
f(x) = 𝑥2+ 2
f(2) = 22+ 2
f(2) = 4 + 2
f(2) = 6
g o f(2) = g(f(2)) =
g(6)
g(x) = 2/𝑥
g(6) = 2/6
g(6) = 1/3

9. 23. What is the y-
intercept of 𝑓(𝑥) =
2𝑥2
− 6𝑥 + 5?
A. 2
B. 6
C. -5
D. 5
The y-intercept is the point on the
graph of a function when it crosses
the y-axis
This is represented by the ordered pair (0, y),
where x is 0
Hence, we evaluate the function 𝑓(𝑥) = 2𝑥2 − 6𝑥 + 5 when
x = 0
𝑓(0) = 2 0 2
− 6(0) + 5
𝑓(0) = 5

10. 24. A Suzuki car is travelling at a rate of 50
kph. After 2 hours, a Toyota car followed
travelling at a rate of 75 kph. How long is it
before the Toyota overtakes the Suzuki?
A. 3
hours
B. 4
hours
C. 5
hours
D.6
hours
R = D/t t = D/R D = Rt
In order for Toyota to overtake Suzuki, their distance travelled
should be equal
𝐷𝑇𝑜𝑦𝑜𝑡𝑎 = 𝑅𝑇𝑜𝑦𝑜𝑡𝑎𝑡𝑇𝑜𝑦𝑜𝑡𝑎 = 𝐷𝑆𝑢𝑧𝑢𝑘𝑖 = 𝑅𝑆𝑢𝑧𝑢𝑘𝑖𝑡𝑆𝑢𝑧𝑢𝑘𝑖
Let x be the time travelled by Suzuki when Toyota overtook it.
𝐷𝑇𝑜𝑦𝑜𝑡𝑎 = 75 𝑥 − 2 = 𝐷𝑆𝑢𝑧𝑢𝑘𝑖 = 50(𝑥)
75 𝑥 − 2 = 50(𝑥)
75𝑥 − 150 = 50𝑥
75𝑥 − 50𝑥 = 150
25𝑥 = 150
25 25
𝑥 = 6

11. 26. How long will it take A and B together, to
finish a job which can be done by A alone in six
days and B alone in three days?
A. 2 ½ days
B. 2 days
C. 4 days
D.3 days
1 day work for A is 1/6 of the job done
1 day work for B is 1/3 of the job done
Combining their work to complete the
job we have
1
6
+
1
3
𝑥 = 1 x is the time required to
complete the job
1
6
+
2
6
𝑥 = 1
3
6
𝑥 = 1
𝑥 = 1
6
3
𝑥 = 2

12. 27. A farm has chickens and pigs. Mercy
counted a total of 32 heads and 100 legs. How
many pigs were in the farm?
A. 14
B. 20
C. 18
D.12
Let x be the number of pigs and y the number of
chickens
x + y = 32 → Eqn 1 Total number of animals
4x + 2y = 100 → Eqn 2
(x + y = 32)2 → 2x +2y
= 64
Equivalent to Eqn 1
4x + 2y = 100
2x + 2y =
64
Subtract Eqn 1 from Eqn 2
2x + 0y =
36
2x = 36
2 2
x = 18

13. 29. The numerator of a fraction is 3 less than
the denominator. If the numerator and
denominator are each increased by 1, the value
of the fraction becomes 3/4. What is the original
fraction?
A. 9/12
B. 6/13
C. 7/12
D.8/11
Let x be the denominator
𝑥− 3
𝑥
𝑥−3+1
𝑥+1
=
3
4
The numerator of a fraction is 3 less than the
denominator
If the numerator and denominator are each
increased by 1, the value of the fraction
becomes 3/4
4(x-3+1) =
3(x+1)
Cross multiply
(4x-12+4) =
3x+3)
Distribute
4x-3x = 3+12 -
4)
x = 11
11− 3
11
=
8
11

14. 31. Find the value of x in the given figure
A. 50
B. 75
C. 55o
D.110o
The sum of the arcs is
360
110𝑜
x is an inscribed angle of the
circle
The measure of an inscribed
angle of a circle is half the
intercepted arc
x = 110/2 = 55 degrees

15. 34. The length of the leg of a right triangle
opposite an angle with measure of 30 degrees is
10. Find the length of its hypotenuse.
A. 5
B. 10
C. 5 3
D.20
30𝑜
60𝑜
ℎ
In a 30-60-90 triangle, the
length opposite the 30 degree
angle is half the hypotenuse
(h)
𝑎 = ℎ/2
𝑏 = 𝑎 3
a = h/2 or h = 2a
Since a = 10, then h = 2(10) =
20
90𝑜

16. 37. Lito wants to use square tiles to cover his
2.4 m by 3.2m bathroom. If the tile is 8 cm on
one side, how many tiles will he need?
A. 96 tiles
B. 120 tiles
C. 1,200
tiles
D.960 tiles
The dimension of the bathroom is 320
x 240 cm
3.2 𝑚 = 320 𝑐𝑚
2.4
𝑚
=
240
𝑐𝑚
The dimension of each tile is 8 x 8 cm
No. of tile for the length = 320/8 = 40
No. of tile for the width = 240/8 = 30
Total number of tiles = 40 x 30 = 1200
tiles

17. 38. What is volume of a
cylinder with a height of 20cm
and base radius of 5cm?
A. 100𝜋 cm3
B. 200𝜋 cm3
C. 500𝜋 cm3
D.400𝜋 cm3
𝑉 = 𝜋𝑟2ℎ
𝑉 = 𝜋52(20)
𝑉 = 𝜋25 (20)
𝑉 = 500 𝜋 cm3

18. 40. A 10 meter board leans against the wall.
The foot of the board is 8 meters from the wall.
How far up the wall does the board reach?
A. 10
meters
B. 4 meters
C. 6 meters
D.8 meters
ℎ2 = 𝑎2 + 𝑏2
8 𝑚
𝑥
102 = 82 + 𝑥2
𝑥2
= 102
− 82
𝑥 = 102− 82
𝑥 = 100 − 64
𝑥 = 36
𝑥 = 6
𝑃𝑦𝑡ℎ𝑎𝑔𝑜𝑟𝑒𝑎𝑛 𝑇ℎ𝑒𝑜𝑟𝑒𝑚
𝑃𝑦𝑡ℎ𝑎𝑔𝑜𝑟𝑒𝑎𝑛 𝑇𝑟𝑖𝑝𝑙𝑒𝑠
3,4,5 = 6,8,10 = 9,12,15
5,12,13 7,24,25 8,15,17

19. 41. The measure of an angle is 15 less than its
complement. What is the measure of the larger
angle?
A. 145
B. 125
C. 55
D.35
Let x be the measure of the angle and y the measure of its
complement
Two angles are complementary to each other if their sum
is 90 degrees
x + y = 90 Eqn
1
x = y - 15
Eqn 2
(y – 15) + y =
90
Substitute x in
Eqn 1
2y – 15 = 90
2y = 90 + 15
2y = 105
2 2
y = 52.5

20. 42. Angle A is 30 more than twice angle B. If
the angles are complementary, what is the
measure of angle A?
A. 20
B. 70
C. 60
D.140
Let A be the measure of the angle and B the measure of its
complement
A = 2B + 30 Eqn
1
A + B = 90 Eqn 2
2B + 30 + B = 90 Substitute Eqn 1 in
Eqn 2
3B = 90 - 30
3B = 60
3 3
B = 20
A = 2(20) + 30 Substitute B in Eqn 1
A = 70

21. 46. A garden is an equilateral triangle in
shape. One side is 13 feet. How many meters of
short fencing are needed to enclose the garden?
A. 17
feet
B. 39
feet
C. 52
feet
D.51
feet
13 𝑚
13 𝑚

22. 47. A wooden plank has dimensions 2 ft by
1.5 ft by 6 inches. What is the volume in
cubic inches?
A. 2,592 cu.in
B. 108 cu.in
C. 1.5 cu.in
D.216 cu.in
2 ft = 24
inches
6
inches
24 x 18 x 6 = 2592 cu. in.

23. 49. The perimeter of a school ground is 480
meters. If the width is 15 meters, what is the
length of the school ground?
A. 200
meters
B. 465
meters
C. 450
meters
D.225
meters
W
=
15
m
L
P = 2W +
2L
480 = 2(15) +
2L
480 = 30 + 2L
480 - 30 = 2L
450 = 2L
450/2 = L
225 = L

24. 50. A picture 10 cm x 8 ½ cm is mounted on a
piece of hard cardboard. If there is a margin of 2
½ cm around the picture, what is the perimeter
of the cardboard used?
A. 47 cm
B. 57 cm
C. 37 cm
D.67 cm
2.
5
2.
5
10
8.5
P = 2W +
2L
P = 2(8.5+5) + 2(10+5)
P = 2(13.5) + 2(15)
P = 27 + 30
P = 57

25. 51. A room of 10m by 7m there is a 7.5m by 5m
carpet in the middle. What percent of the room
is uncovered?
A. 46.4%
B. 53.6%
C. 48%
D.80%
Area of the room = 10 x 7
= 70
Area of the carpet = 7.5 x 5 =
37.5
Area of the room uncovered = 70 – 37.5
= 32.5
Percent of the room uncovered = 32.5/70 = 0.4642 x
100 = 46.4%

26. 55. What is the volume of air in a
spherical balloon with a diameter of
24 cm?
A. 2304 π cm3
B. 18432 π
cm3
C. 240 π cm3
D.144 π cm3
V =
4
3
𝜋𝑅3
V =
4
3
𝜋123
D = 2R =
24
R = 24/2 =
12
V =
4
3
𝜋123
V =2304𝜋 cm3

27. 58. Find the area of a trapezoid whose
median and altitude have lengths 15 and
18, respectively.
A. 270
B. 135
C. 66
D.Cannot be
determined
from the
given
information
18
1
5
A =
𝑎+𝑏
2
ℎ
A = median x ℎ
A = 15 x 18
A = 270

28. 59. What is the area of an isosceles triangle
whose base is 10 and its base angle is 60
degrees?
A. 25 3
B. 50 3
C. 25
D.50
60𝑜
10
30𝑜
60𝑜
60𝑜
10
5
5 3
A =
1
2
𝑏ℎ
A =
1
2
(10)(5 3)
A =
1
2
(10)(5 3)
5
A = (5)(5 3)
A = 25 3)

29. 60. In the given figure, the smaller square is
inscribed in the circle, and the circle is inscribed
in the larger square. If the circumference of the
circle is 4π, what is the difference in the areas of
the larger square and the smaller square?
A. 4
B. 8
C. 4𝜋
D.8𝜋
C = 2𝜋r
4𝜋 = 2𝜋r
2𝜋
2𝜋
2 = 𝑟
𝑟 = 2 Diagonal of the small
square = 4
d = s 2 = 4
s 2 = 4
(𝑠 =4/ 2)
(𝑠2
= 42
/ 2
2
)
𝑠2
=16/2
𝑠2
= 8
𝑠 = 4
Area of big square = (𝑠)2 = (4)2=
16
𝐴𝐵𝑖𝑔 − 𝐴𝑆𝑚𝑎𝑙𝑙 = 16 − 8 = 8
2 2
(𝑠 =4/ 2)
2

30. 8. Car A travelling at a rate of 70 kph leaves the
house 2 hours after car B has left and overtakes
it in 5 hours. At what rate was the car B
travelling?
A. 40 kph
B. 30 kph
C. 50 kph
D.20 kph
R = D/t t = D/R D = Rt
In order for CAR A to overtake CAR B, their distance travelled should
be equal
𝐷𝐴 = 𝑅𝐴𝑡𝐴 = 𝐷𝐵 = 𝑅𝐵𝑡𝐵
Let x be the RATE of car B.
𝑅𝐴𝑡𝐴 = 𝑋𝐵𝑡𝐵
70(5) = 𝑋𝐵(7)
70(5) = 𝑋𝐵(7)
7
7
10(5) = 𝑋𝐵 𝑋𝐵 = 50

31. 14. Two times a certain number added to 30
gives the same result as three times the same
number subtracted from 90. What is the
number?
A. 20
B. 30
C. 15
D.12
Let x be the number
2x + 30 = 90 - 3x
2x + 3x = 90 -
30
Group similar terms
5x =
60
5 5
x = 12

32. 30. Find the value of x.
A. 9
B. 24
C. 30
D.32
7x + 54 3x + 90
When 2 lines intersect, the
angles formed opposite to
each other are congruent
(measures are equal).
7x + 54 = 3x +
90
7x -3x = 90 - 54
4x = 36
4 4
x = 9
Vertical Angles

33. 32. In parallelogram ABCD, angle A is three
times angle B. What is the measure of angle
B?
A. 30
B. 45
C. 50
D.135
A B
C
D
In parallelograms, adjacent
angles are supplementary or A
+ B = 180
A = 3B
A + B =
180
3B + B =
180
4B = 180
4 4
B = 45

34. 56. A square has a diagonal with length of
6. Find its area.
A. 9
B. 36
C. 18
D.72
𝑑 = 𝑠 2
6 = 𝑠 2
2
2
s = 6/ 2
s = 6/ 2
s
=
6/
2 Area = 𝑠2
= 6/ 2
2
Area = 𝑠2
= 36/2
Area = 𝑠2
= 18
Pythagorean
Theorem
𝑎
𝑏
=
𝑎
ℎ2 = 𝑎2 + 𝑏2
ℎ2 = 𝑎2 + 𝑎2
ℎ2 = 2𝑎2
62
= 2𝑎2
36 = 2𝑎2
2
2
18 = 𝑎2

35. 57. Find the area of an
equilateral triangle with a
perimeter of 9.
A. 4.5
B. 81 3
2
C. 9 3
4
D.40.5
Perimeter
= 9
Side = 9/3 =
3
3
60𝑜
60𝑜
60𝑜
Equilateral
=
Equiangula
r
30𝑜
3
A =
1
2
𝑏ℎ
In a 30-60-90 triangle, the
length opposite the 30 degree
angle is half the hypotenuse
(h)
1.5=3/
2
In a 30-60-90 triangle, the
length opposite the 60 degree
angle is a 3
3
2
3
A =
1
2
𝑏ℎ
A =
1
2
(3)(
3
2
3)
A = (
9
4
3)
A =
9 3
4