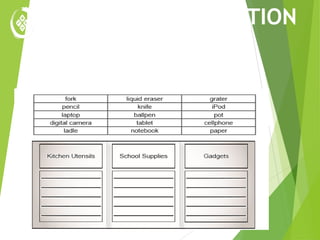
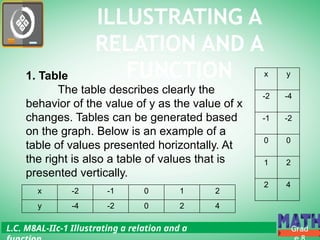
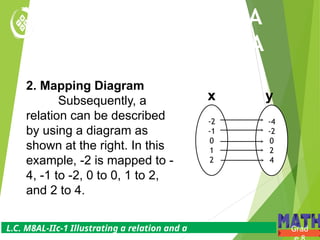
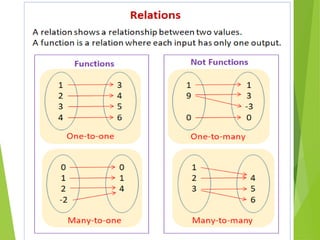
The document outlines the key concepts of relations and functions in mathematics, focusing on linear inequalities, ordered pairs, domains, and ranges. It provides examples and activities to illustrate the relationship between variables through practical scenarios, such as calculating earnings based on hours worked. Additionally, it emphasizes that all functions are relations, but not all relations are functions, teaching students how to classify and represent them in various forms.