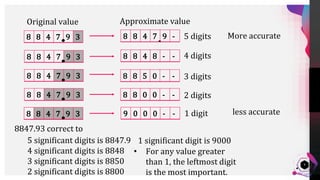
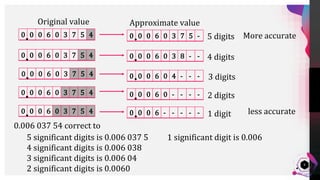
This document is a chapter from a mathematics textbook about significant figures and scientific notation. 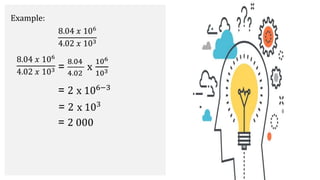It includes examples of: - Determining the number of significant figures in measurements like 12.3 units and 0.048 g - Approximating values like 8847.93 m to different degrees of accuracy by truncating digits - Applying the rules for significant figures to calculations involving quantities with differing degrees of precision - Expressing very large and small numbers using scientific notation, like writing 5.3 × 101 and 0.000387 × 101 The document provides guidance and practice problems to help students learn how to determine the number of significant figures and express values in scientific notation.

1. MATHEMATICS 7
CHAPTER 3. LESSON 2

2. Jens
Martensson
SIGNIFICANT
FIGURES
In this lesson, you will be able to …
2
⮚Determine a significant
digit in a given situation

3. Jens
Martensson
3
In fact, the height of this mountain can also be
expressed as follows:
Mount Everest is the highest mountain in the
world. According to a survey in 2005, its height is
8847.93 m including in the snow.
a. 8847.9 m (correct to the nearest 0.1m)
b. 8848 m (correct to the nearest m)
c. 8850 m (correct to the nearest 10 m)
d. 8800 m (correct to the nearest 100 m)
e. 9000 m (correct to the nearest 1000 m)
More Accurate
Less Accurate

4. Jens
Martensson
4
Original value Approximate value
8 8 4 7 9 3 8 8 4 7 9 -
8 8 4 7 9 3 8 8 4 8 - -
8 8 4 7 9 3 8 8 5 0 - -
8 8 4 7 9 3 8 8 0 0 - -
8 8 4 7 9 3 9 0 0 0 - -
5 digits
4 digits
3 digits
2 digits
1 digit
More accurate
less accurate
8847.93 correct to
5 significant digits is 8847.9
4 significant digits is 8848
3 significant digits is 8850
2 significant digits is 8800
1 significant digit is 9000
• For any value greater
than 1, the leftmost digit
is the most important.

5. Jens
Martensson
5
Guidelines in finding the number of significant figures.
1. All nonzero digits are significant.
Ex: 12.3 units
35.46 units
3 significant figures
4 significant figures
2. Zero between two other significant
digits are significant.
Ex: 5.048 g 4 significant figures
3. Zeros that precede the first
nonzero digit and tell the location of
the decimal point are not significant.
Ex: 0.053 g 2 significant figures
4. Zeros at the end of a number
may or may not be significant.
Zeros at the end of a number are
significant if they are to the right of
the decimal point.
Ex: 0.6090 mL
2 000 cm
4 SF
1 SF

6. Jens
Martensson
6
0 0 0 6 0 3 7 5 4
Original value Approximate value
0 0 0 6 0 3 7 5 -
0 0 0 6 0 3 7 5 4 0 0 0 6 0 3 8 - -
0 0 0 6 0 3 7 5 4 0 0 0 6 0 4 - - -
0 0 0 6 0 3 7 5 4 0 0 0 6 0 - - - -
0 0 0 6 0 3 7 5 4 0 0 0 6 - - - - -
3 digits
2 digits
1 digit
More accurate
less accurate
4 digits
5 digits
0.006 037 54 correct to
5 significant digits is 0.006 037 5
4 significant digits is 0.006 038
3 significant digits is 0.006 04
2 significant digits is 0.0060
1 significant digit is 0.006

7. Jens
Martensson
7
Example:
The selling price for 300 g of tea is P807.50. Find the average selling price
for 1g of tea, correct to:
a. 3 significant digits b. 2 significant digits
a. Average selling price for 1 g of tea
Correct to 3 significant digit
Correct to 2 significant digit

8. Jens
Martensson
SCIENTIFIC
NOTATION
In this lesson, you will be able to …
8
⮚Write very large or
very small numbers in
scientific notation

9. Jens
Martensson
9
Scientific Notation
Example:
5.3 =
87 =
68 000 =
0.49 =
0.000 387 5 =
How about 270 000?
How about 0.000 000 000 000 000 019 9?
⮚ 25 000 000 000
⮚ 0.074

10. Jens
Martensson
10
Example:
= 45
= 45
= 0.045

11. Jens
Martensson
11
Example:

12. Thank You
and
Godbless!