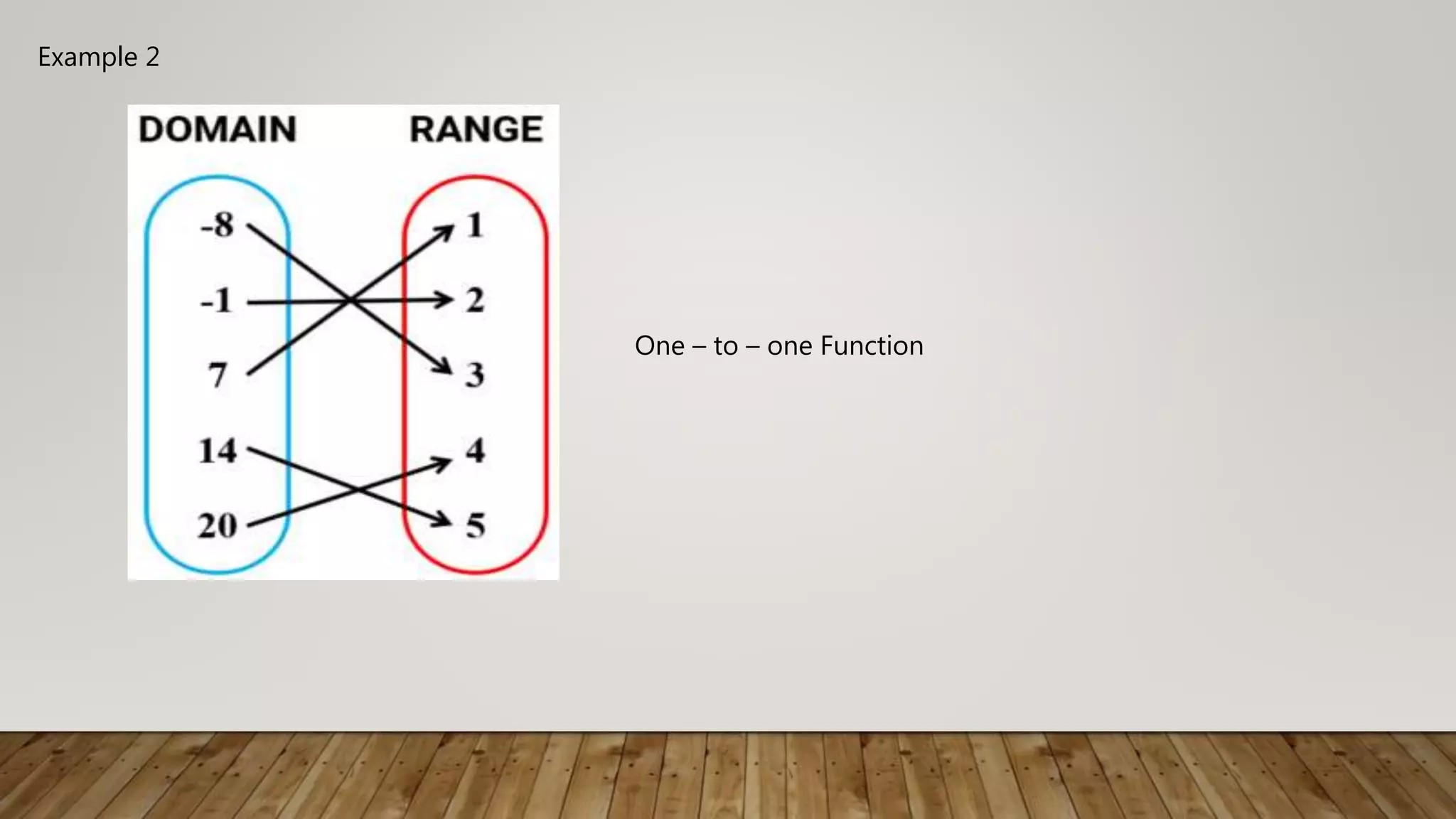
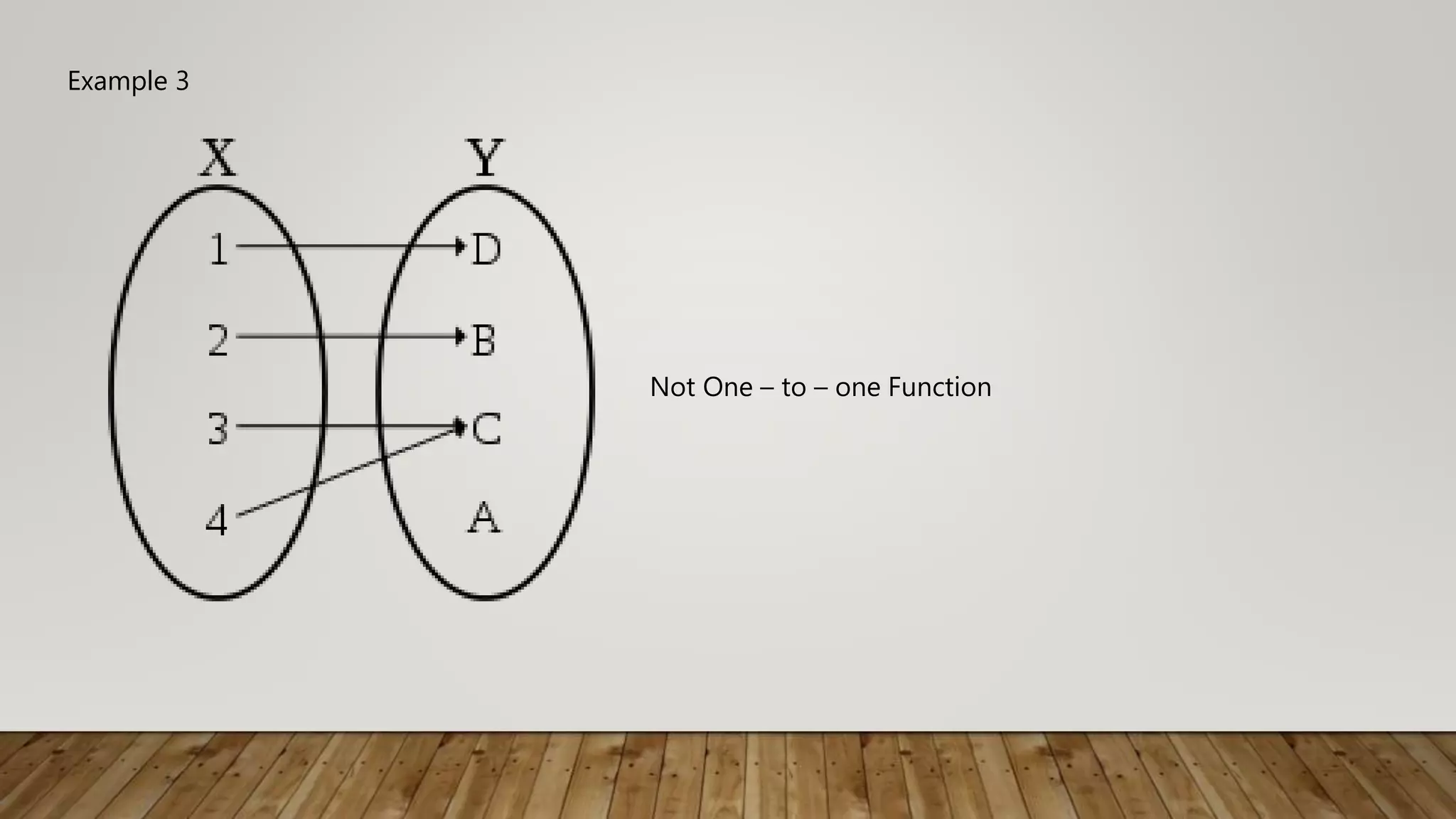
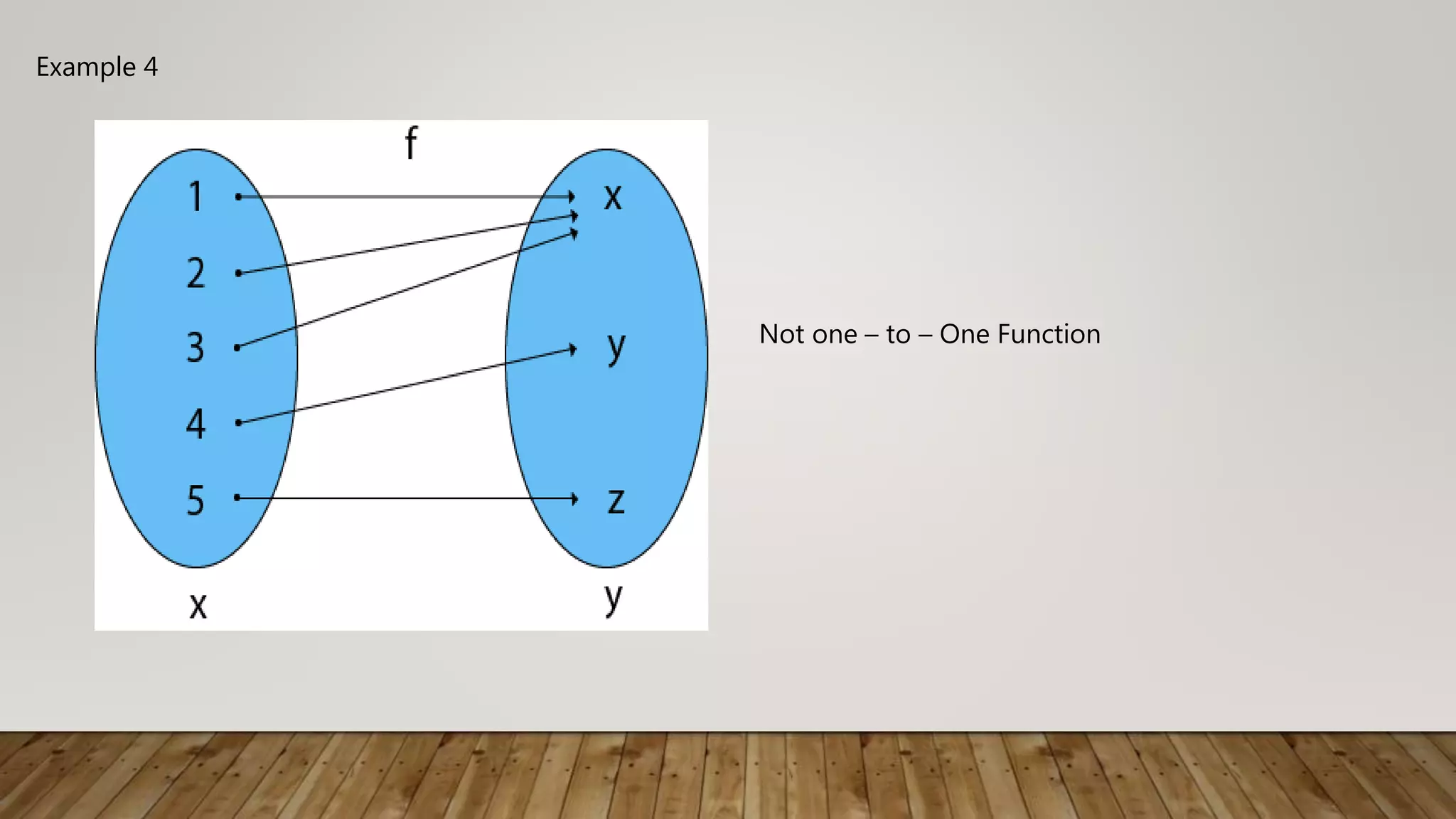
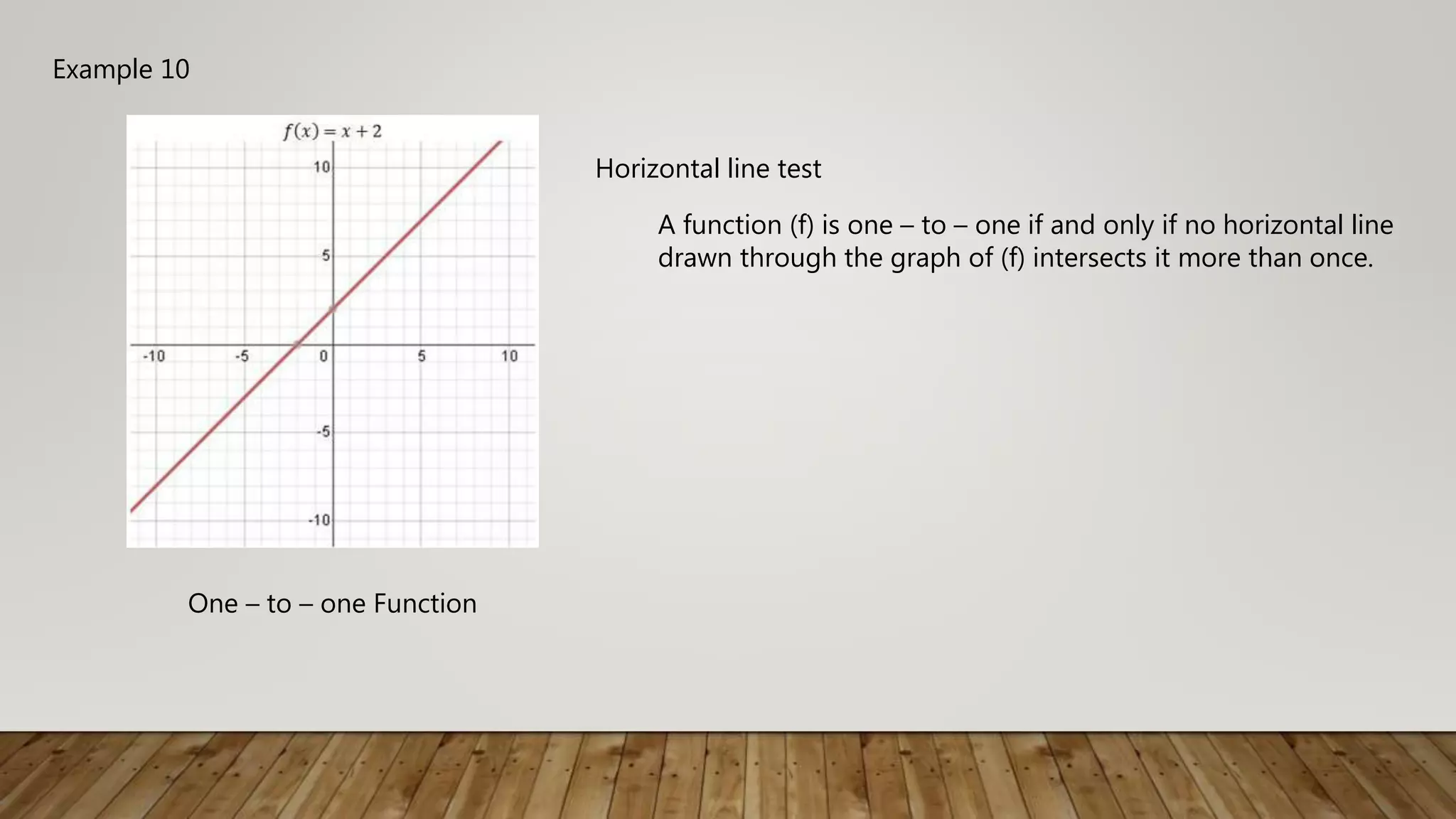
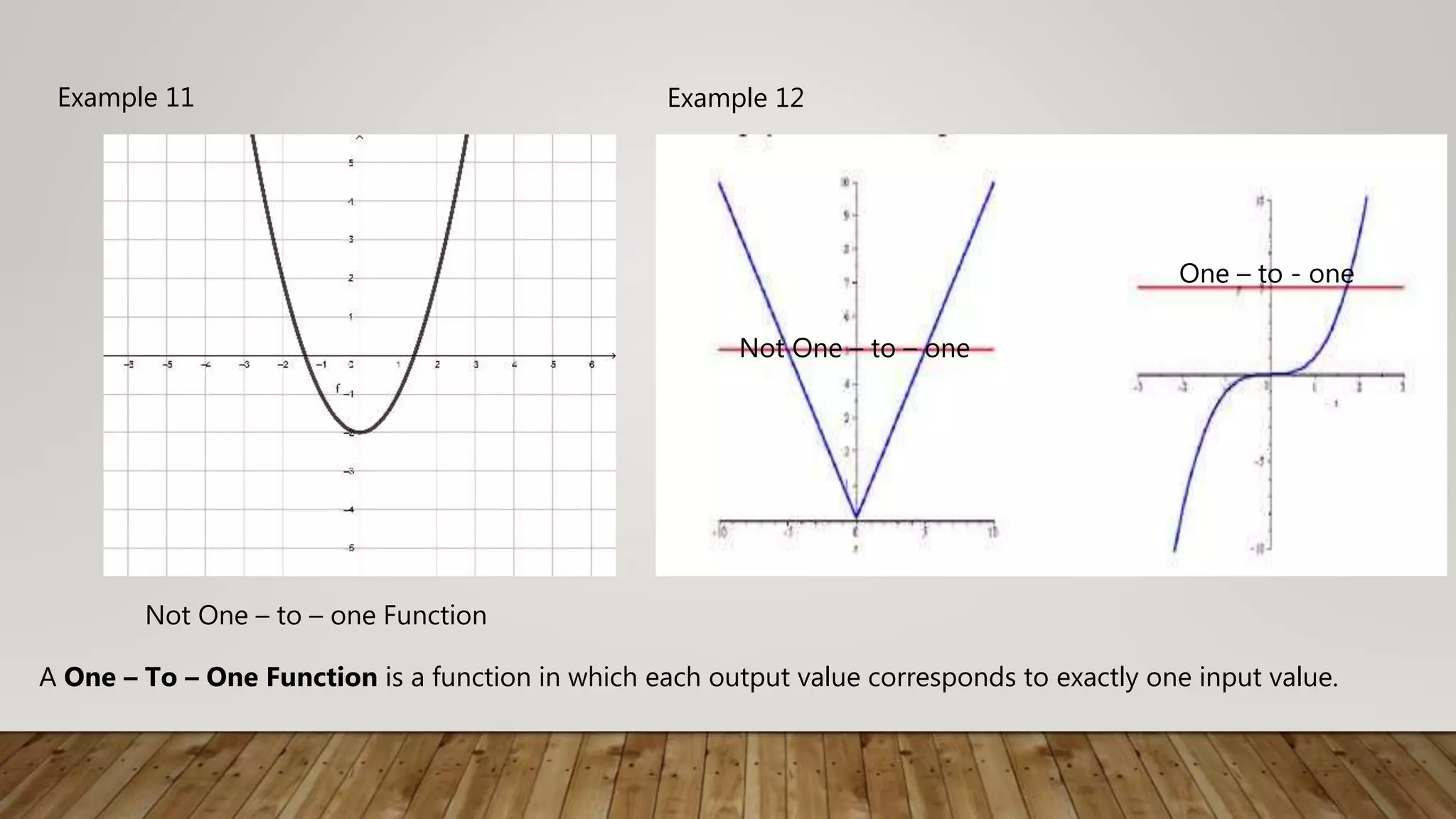
The document defines and provides examples of one-to-one functions. A function is one-to-one if each element of the domain maps to a unique element in the range, and vice versa. This can be tested graphically using the horizontal line test, where no horizontal line intersects the graph in more than one point. Examples demonstrate one-to-one functions, including linear functions like f(x)=2x-5, and non one-to-one functions where the highest degree of an even polynomial allows multiple inputs to map to the same output.

1. INVERSE OF ONE-
TO-ONE FUNCTION
ONE – TO – ONE FUNCTION

2. Target Goals :
I can define a one-to-one functions.
I can illustrates a one-to-one function.
I can use horizontal line test in determining whether the graph is a one – to –
one function or not.

3. One-To-One Function
- A relation is one-to-one function if and only if each element of its domain corresponds to a unique
element in its range, and each element of its range corresponds to a unique element in its domain.
- In other words, when a function has additional property that no two unique elements of the
domain have the same image in the range, the function is said to be one-to-one.
Example 1
One – to – one Function

4. Example 2
One – to – one Function

5. Example 3
Not One – to – one Function

6. Example 4
Not one – to – One Function

7. Example 5
( 1 ,2) (3 , 4) (5 , 6) (7 , 8) (9 , 10) One – to – one Function
Example 6
(1 , 2) ( 3 , 2) ( 4 , 5) ( 6 , 7) ( 8 , 2 ) Not One – to – one function
Example 7
One – to – one Function

8. Example 8
One – to – one Function
Example 9
x 2 3 4 5 6
y 3 5 7 2 3
Not One – to – one function

9. Example 10
Horizontal line test
A function (f) is one – to – one if and only if no horizontal line
drawn through the graph of (f) intersects it more than once.
One – to – one Function

10. Example 11
Not One – to – one Function
Example 12
Not One – to – one
One – to - one
A One – To – One Function is a function in which each output value corresponds to exactly one input value.

11. Example 13
f (x) = 2x - 5 One – to – one function
f (x1) = f (x2 )
2x1 – 5 = 2x2 - 5
2x1 – 5 + 5 = 2x2
2x1 = 2x2
2𝑥1
2
=
2𝑥2
2
x1 = x2
Example 14
f (x) = x4 + 3 Not one-to-one function
Example 15
f (x) = x + 5 One – to – one function
Example 16
f (x) = x2 + 3 Not one- to- one function
Note: When the given problem is an equation the best thing to determine whether it is a one – to – one
function or not, just observe their highest degree of function when it is an even number there is no one
- to – one function but when it is odd it is a one – to – one function.