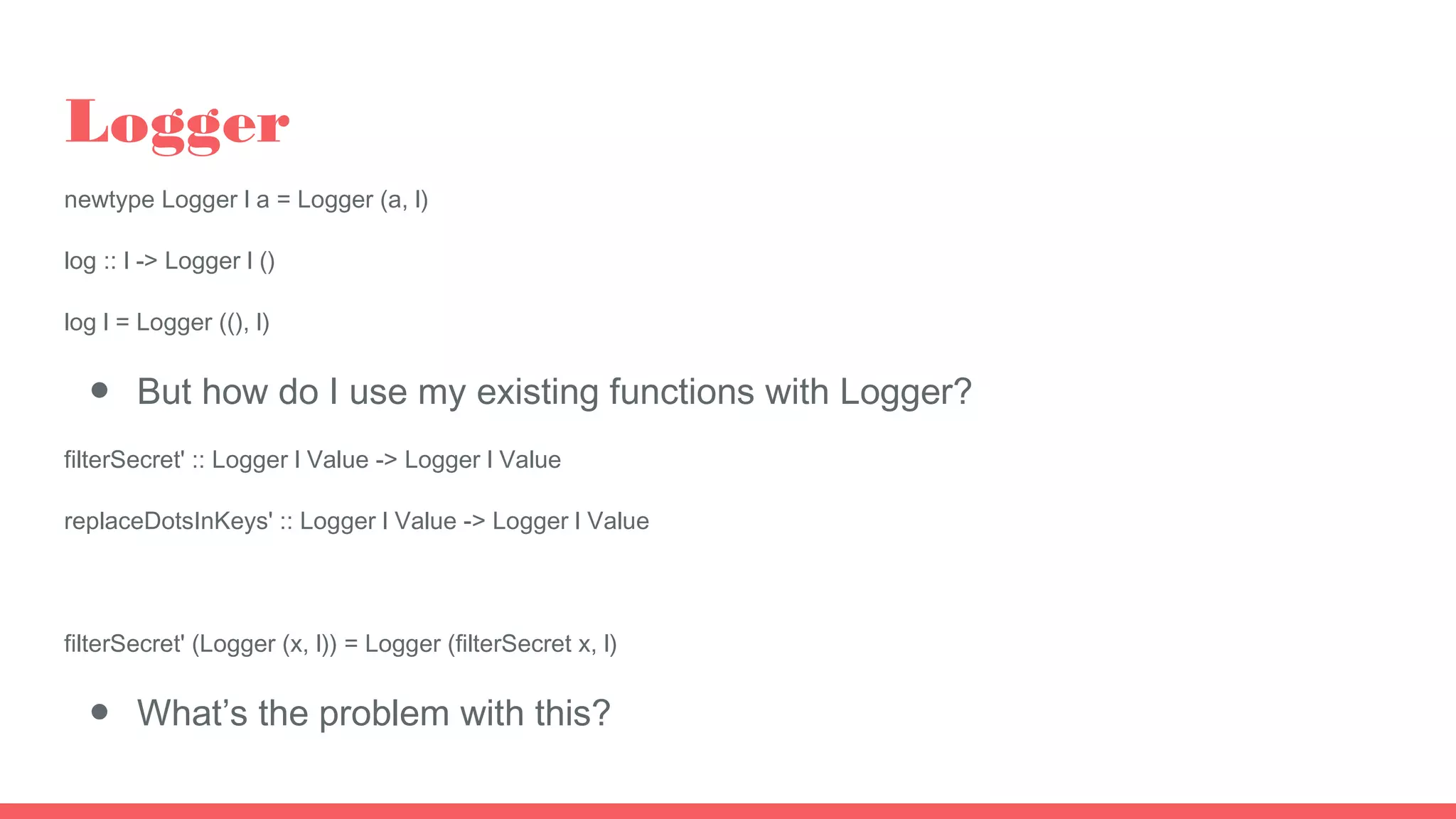
The document discusses functors, applicatives, and monads in Haskell. It provides examples of how functors allow lifting functions to work on container types like Maybe and Logger using fmap. Applicatives allow applying functions to multiple arguments within a container using <*>. Monads generalize applicatives by allowing chained computations through >>= and return, handling context and effects like logging.

1. Functors,
Applicatives,
Monads
Motivation

2. Functors, Applicatives, Monads
● Why Oh Why?
● I am going back to PHP
● Gimme my imperative code back
● Let me get my PhD first

3. Why should I bother?
7 ± 2
The Magical Number Seven, Plus or Minus Two - George Miller
Surface Area vs Volume

4. Functions vs Subroutines
int square(int n)
square :: Int -> Int

5. Functions vs Subroutines
● Totality
● Determinism
● Purity
● Parameters
● Results
● Composition

6. Function Composition
● Build larger programs by composing smaller functions together
xs = [1, 2, 3, 4, 5]
stddev xs = sqrt . average . map (square . (mu -)) xs
pyth x y = sqrt (square x + square y)
● How does values flow from function to function?

7. Functions vs Subroutines
But real world programs are not like this.
1. Null handling
2. Exceptions
3. Logging
4. IO
● Simple function composition breaks down in these cases

8. Example
replaceDotsInKeys :: Value -> Value
replaceDotsInKeys = ...
filterSecret :: Value -> Value
filterSecret = ...
processValue :: Value -> Value
processValue = replaceDotsInKeys . filterSecret

9. Logger
newtype Logger l a = Logger (a, l)
log :: l -> Logger l ()
log l = Logger ((), l)
● But how do I use my existing functions with Logger?
filterSecret' :: Logger l Value -> Logger l Value
replaceDotsInKeys' :: Logger l Value -> Logger l Value
filterSecret' (Logger (x, l)) = Logger (filterSecret x, l)
● What’s the problem with this?

10. Logger
liftLogger :: (a -> b) -> Logger l a -> Logger l b
liftLogger f (Logger (x, l)) = Logger (f x, l)
replaceDotsInKeys' :: Logger l Value -> Logger l Value
replaceDotsInKeys' = liftLogger replaceDotsInKeys

11. Maybe
data Maybe a = Just a | Nothing
● But how do I use my existing functions with Maybe?
filterSecret' :: Maybe Value -> Maybe Value
replaceDotsInKeys' :: Maybe Value -> Maybe Value
filterSecret' (Just x) = Just (filterSecret x)
filterSecret' Nothing = Nothing
● What’s the problem with this?

12. Maybe
liftMaybe :: (a -> b) -> Maybe a -> Maybe b
liftMaybe f (Just x) = Just (f x)
liftMaybe f Nothing = Nothing
replaceDotsInKeys' :: Maybe Value -> Maybe Value
replaceDotsInKeys' = liftMaybe replaceDotsInKeys

13. Functors
class Functor f where
fmap :: (a -> b) -> f a -> f b
instance Functor (Logger l) where
fmap f (Logger (x, l)) = Logger (f x, l)
instance Functor Maybe where
fmap f (Just x) = Just (f x)
fmap f Nothing = Nothing

14. Functors
processValue' :: Logger l Value -> Logger l Value
processValue' = fmap (replaceDotsInKeys . filterSecret)
processValue' :: Maybe Value -> Maybe Value
processValue' = fmap (replaceDotsInKeys . filterSecret)
processValue' :: Functor f => f Value -> f Value
processValue' = fmap (replaceDotsInKeys . filterSecret)

15. Functions with multiple arguments
fmap :: (a -> b) -> Logger l a -> Logger l b
(+) :: (Int -> (Int -> Int))
x :: Logger l Int
y :: Logger l Int
fmap (+) x :: Logger l (Int -> Int)
fmap (+) x y :: ???
● We need something that can do
Logger l (a -> b) -> Logger l a -> Logger l b

16. Applicative
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
instance Monoid l => Applicative (Logger l) where
pure x = Logger (x, mempty)
Logger (f, l) <*> Logger (x, l') = Logger (f x, l `mappend` l')

17. Applicative
(fmap (+) (pure 1)) <*> (pure 2) = pure 3
(+) <$> (pure 1) <*> (pure 2) = pure 3
((+) $ 1) $ 2 = 3
f <$> (pure x) <*> (pure y) <*> (pure z) = pure (f x y z)
f <$> (g x) <*> (h y) = do { a <- g x; b <- h y; pure (f a b) }

18. I want more!
Double f(String name)
{
Double val = hashmap.lookup(name);
Double result = sqrt(val);
log(....);
return result;
}

19. Contextual Computation
lookup :: String -> Logger l Double
sqrt :: Double -> Logger l Double
f :: String -> Logger l Double
● We are back to our composition problem

20. Contextual Computation
f name = lookup name `bind` sqrt
bind :: Monoid l => Logger l a -> (a -> Logger l b) -> Logger l b
bind (Logger (x, l)) f = let Logger (y, l') = f x
in Logger (y, l `mappend` l')

21. Monads
class Applicative m => Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
instance Monoid l => Monad (Logger l) where
return = pure
Logger (x, l) >>= f = let Logger (y, l') = f x
in Logger (y, l `mappend` l')

22. Comparison
fmap :: (a -> b) -> m a -> m b
<*> :: m (a -> b) -> m a -> m b
=<< :: (a -> mb) -> m a -> m b
● How do these compare with each other?