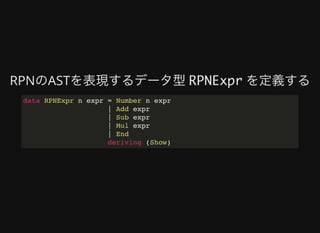
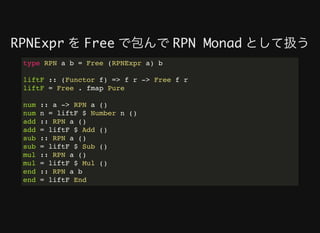
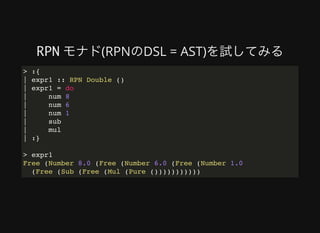
1. Free monads allow defining monadic interpreters for domain-specific languages (DSLs) by representing the DSL's abstract syntax tree as a recursive data type and making it an instance of the Functor typeclass. 2. The document provides an example of defining a DSL for reverse polish notation (RPN) expressions using a Free monad. This includes defining the RPNExpr data type, making it a Functor, lifting it into a Free monad, and writing functions for evaluation, parsing, and pretty-printing RPN expressions. 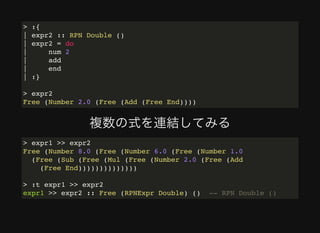3. By defining the interpreter as a monad, the RPN expressions can be combined in a composable manner while retaining the ability to run,

1. Free Monads
Getting Started

2. Self-introduction
/laʒenɔʁɛ̃k/ カマイルカlagénorhynque
(defprofile lagénorhynque
:name "Kent OHASHI"
:account @lagenorhynque
:company "Opt, Inc."
:languages [Clojure Haskell Python Scala
English français Deutsch русский]
:interests [programming language-learning mathematics]
:contributing [github.com/japan-clojurians/clojure-site-ja])

3. Contents
1. What are monads?
2. What are Free monads?
3. Example: RPN expressions

4. What are monads?

5. de nition of Monad
cf.
GHC.Base#Monad
class Applicative m => Monad m where
(>>=) :: forall a b. m a -> (a -> m b) -> m b
(>>) :: forall a b. m a -> m b -> m b
m >> k = m >>= _ -> k
{-# INLINE (>>) #-}
return :: a -> m a
return = pure
fail :: String -> m a
fail s = errorWithoutStackTrace s
scalaz/Monad.scala

6. return
値 a をモナド m に⼊れる
Haskell: return
Scalaz: point
a -> m a
A => M[A]

7. bind
値 m a に 関数 a -> m b を適⽤して m b にする
Haskell: >>=
Scalaz: bind (cf. flatMap)
m a -> (a -> m b) -> m b
M[A] => (A => M[B]) => M[B]

8. do notation (Haskell)
↓ desugar
a = Just 2
b = Just 3
c = do
x <- a
y <- b
return $ x * y
a = Just 2
b = Just 3
c = a >>= (x ->
b >>= (y ->
return $ x * y))

9. for expression (Scala)
↓ desugar
val a = Some(2)
val b = Some(3)
val c = for {
x <- a
y <- b
} yield x * y
val a = Some(2)
val b = Some(3)
val c = a.flatMap { x =>
b.map { y =>
x * y
}
}

10. What are Free monads?

11. de nition of Free
cf.
Control/Monad/Free.hs
data Free f a = Pure a | Free (f (Free f a))
instance Functor f => Monad (Free f) where
return = pure
{-# INLINE return #-}
Pure a >>= f = f a
Free m >>= f = Free ((>>= f) <$> m)
scalaz/Free.scala

12. リストのような再帰的データ構造
data [] a = [] | a : [a]
f が Functor ⇒ Free f は Monad
→ Functor のインスタンスを Free で包めば
Monad として扱える
※ GHC拡張で Functor を⾃動導出することも:
DeriveFunctor

13. Example: RPN expressions

14. repositories
cf.
lagenorhynque/freemonad-hs
FreeMonad/RPNExpr.hs
lagenorhynque/freemonad-scala
freemonad/RPNExpr.scala

15. RPN: Reverse Polish Notation
↓ with parentheses
↓ evaluate
逆ポーランド記法 - Wikipedia
8 6 1 - * 2 +
((8 (6 1 -) *) 2 +)
42

16. DSL interpreter
RPN DSL = AST -- Free monad
→ eval :: AST -> Num
→ stringify :: AST -> String
← parse :: String -> AST

17. RPNのASTを表現するデータ型 RPNExpr を定義する
data RPNExpr n expr = Number n expr
| Add expr
| Sub expr
| Mul expr
| End
deriving (Show)

18. RPNExpr を Functor にする
instance Functor (RPNExpr n) where
fmap f (Number n expr) = Number n $ f expr
fmap f (Add expr) = Add $ f expr
fmap f (Sub expr) = Sub $ f expr
fmap f (Mul expr) = Mul $ f expr
fmap _ End = End

19. RPNExpr を Free で包んで RPN Monad として扱う
type RPN a b = Free (RPNExpr a) b
liftF :: (Functor f) => f r -> Free f r
liftF = Free . fmap Pure
num :: a -> RPN a ()
num n = liftF $ Number n ()
add :: RPN a ()
add = liftF $ Add ()
sub :: RPN a ()
sub = liftF $ Sub ()
mul :: RPN a ()
mul = liftF $ Mul ()
end :: RPN a b
end = liftF End

20. RPN モナド(RPNのDSL = AST)を試してみる
> :{
| expr1 :: RPN Double ()
| expr1 = do
| num 8
| num 6
| num 1
| sub
| mul
| :}
> expr1
Free (Number 8.0 (Free (Number 6.0 (Free (Number 1.0
(Free (Sub (Free (Mul (Pure ()))))))))))

21. 複数の式を連結してみる
> :{
| expr2 :: RPN Double ()
| expr2 = do
| num 2
| add
| end
| :}
> expr2
Free (Number 2.0 (Free (Add (Free End))))
> expr1 >> expr2
Free (Number 8.0 (Free (Number 6.0 (Free (Number 1.0
(Free (Sub (Free (Mul (Free (Number 2.0 (Free (Add
(Free End))))))))))))))
> :t expr1 >> expr2
expr1 >> expr2 :: Free (RPNExpr Double) () -- RPN Double ()

22. RPNのASTを⽂字列化する関数 stringify
stringify :: (Show a) => RPN a b -> String
stringify (Free (Number n e)) = show n ++ " " ++ stringify e
stringify (Free (Add e)) = "+ " ++ stringify e
stringify (Free (Sub e)) = "- " ++ stringify e
stringify (Free (Mul e)) = "* " ++ stringify e
stringify (Free End) = "."
stringify (Pure _) = ""

23. > expr1
Free (Number 8.0 (Free (Number 6.0 (Free (Number 1.0
(Free (Sub (Free (Mul (Pure ()))))))))))
> stringify expr1
"8.0 6.0 1.0 - * "
> expr2
Free (Number 2.0 (Free (Add (Free End))))
> stringify expr2
"2.0 + ."
> stringify $ expr1 >> expr2
"8.0 6.0 1.0 - * 2.0 + ."

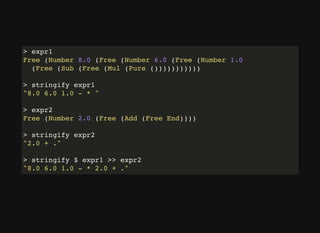
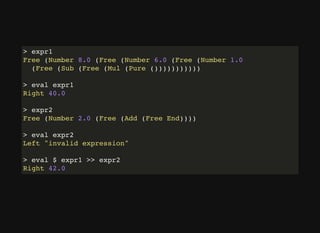
24. ⽂字列をRPNのASTに変換する関数 parse
parse :: (Read a) => String -> Either String (RPN a ())
parse = foldM rpn (Pure ()) . reverse . words
where
rpn e "+" = Right . Free $ Add e
rpn e "-" = Right . Free $ Sub e
rpn e "*" = Right . Free $ Mul e
rpn _ "." = Right $ Free End
rpn e n = case reads n of
[(v,_)] -> Right . Free $ Number v e
_ -> Left "invalid input"

25. > parse "8.0 6.0 1.0 - * " :: Either String (RPN Double ())
Right (Free (Number 8.0 (Free (Number 6.0 (Free (Number 1.0
(Free (Sub (Free (Mul (Pure ())))))))))))
> parse "2.0 + ." :: Either String (RPN Double ())
Right (Free (Number 2.0 (Free (Add (Free End)))))
> parse "8.0 6.0 1.0 - * 2.0 + ." :: Either String (RPN Double ())
Right (Free (Number 8.0 (Free (Number 6.0 (Free (Number 1.0
(Free (Sub (Free (Mul (Free (Number 2.0 (Free (Add
(Free End)))))))))))))))
> parse "2.0 3.0 /" :: Either String (RPN Double ())
Left "invalid input"

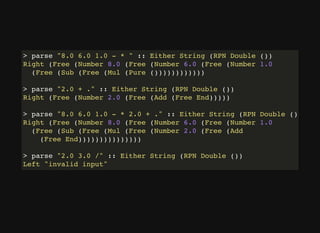
26. RPNのASTを評価する関数 eval
eval :: (Num a) => RPN a b -> Either String a
eval = calc []
where
calc stack (Free (Number n e)) = calc (n : stack) e
calc (n1:n2:ns) (Free (Add e)) = calc (n2 + n1 : ns) e
calc (n1:n2:ns) (Free (Sub e)) = calc (n2 - n1 : ns) e
calc (n1:n2:ns) (Free (Mul e)) = calc (n2 * n1 : ns) e
calc (n:_) (Free End) = Right n
calc (n:_) (Pure _) = Right n
calc _ _ = Left "invalid expression"

27. > expr1
Free (Number 8.0 (Free (Number 6.0 (Free (Number 1.0
(Free (Sub (Free (Mul (Pure ()))))))))))
> eval expr1
Right 40.0
> expr2
Free (Number 2.0 (Free (Add (Free End))))
> eval expr2
Left "invalid expression"
> eval $ expr1 >> expr2
Right 42.0

28. データ型を定義して Functor にすることで、
Free を介して Monad が得られた
例えば
データ型として定義したASTをモナドに
⇒ 合成可能なDSL(= モナド)が提供できる
⇒ AST(= モナド)を解釈する関数群を⽤意する
ことでインタプリタが書ける

29. Further Reading
/
第13章 外部作⽤とI/O
Haskell for all: Why free monads matter
独習 Scalaz
Free Monad
猫番
⾃由モナド (Free)
『Scala関数型デザイン＆プログラミング』
Functional Programming in Scala

30. free: Monads for free
Control/Monad/Free.hs
scalaz/scalaz
scalaz/Free.scala
typelevel/cats
cats/free/Free.scala

31. /
10.1 逆ポーランド記法電卓
14.6 安全な逆ポーランド記法電卓を作ろう
cf.
Interpreter パターン - Wikipedia
『すごいHaskellたのしく学ぼう！』 Learn You a
Haskell for Great Good!
MP in Scala
MP in Haskell
Functor, Applicative, Monadのシンプルな定式化