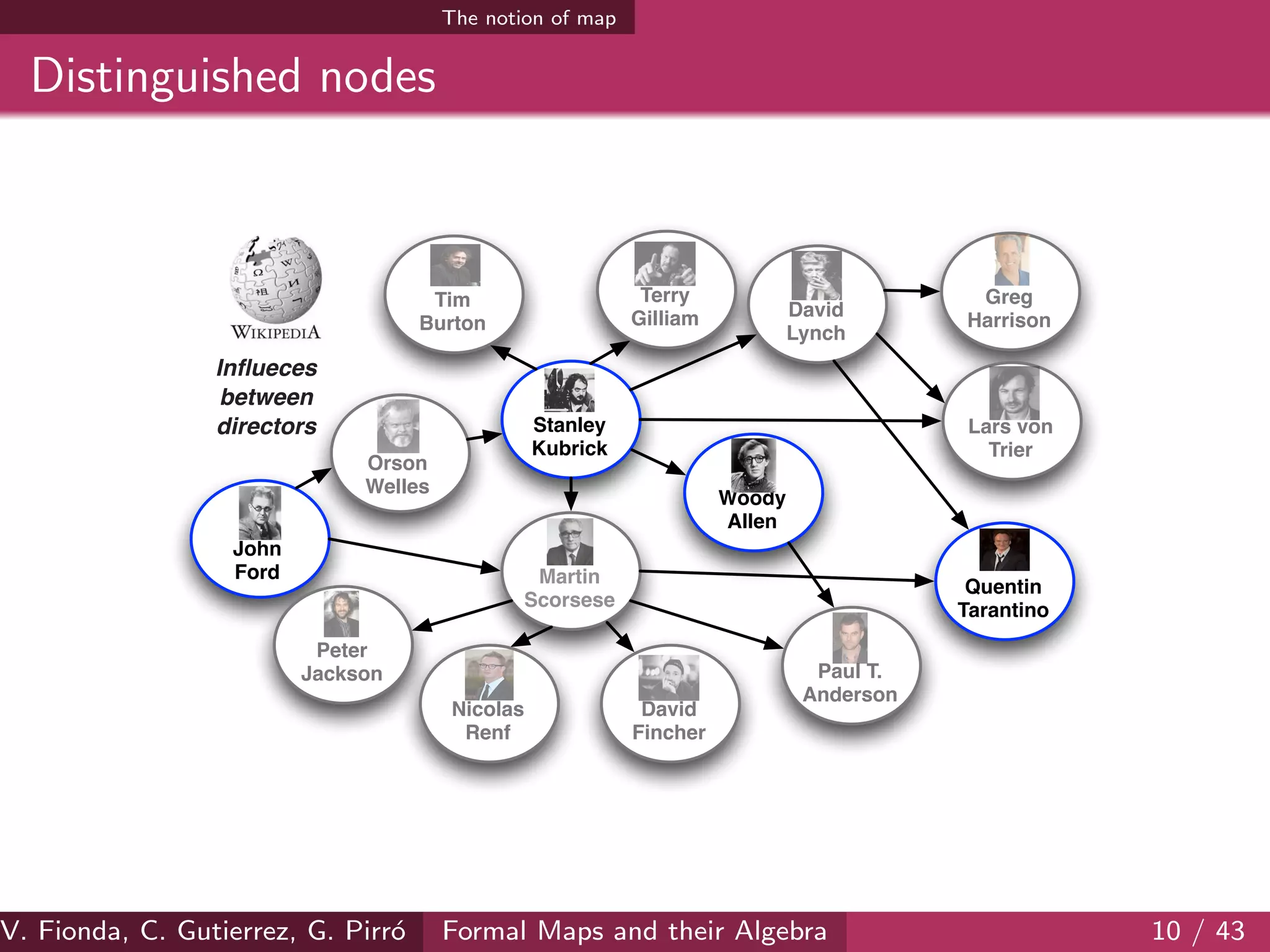
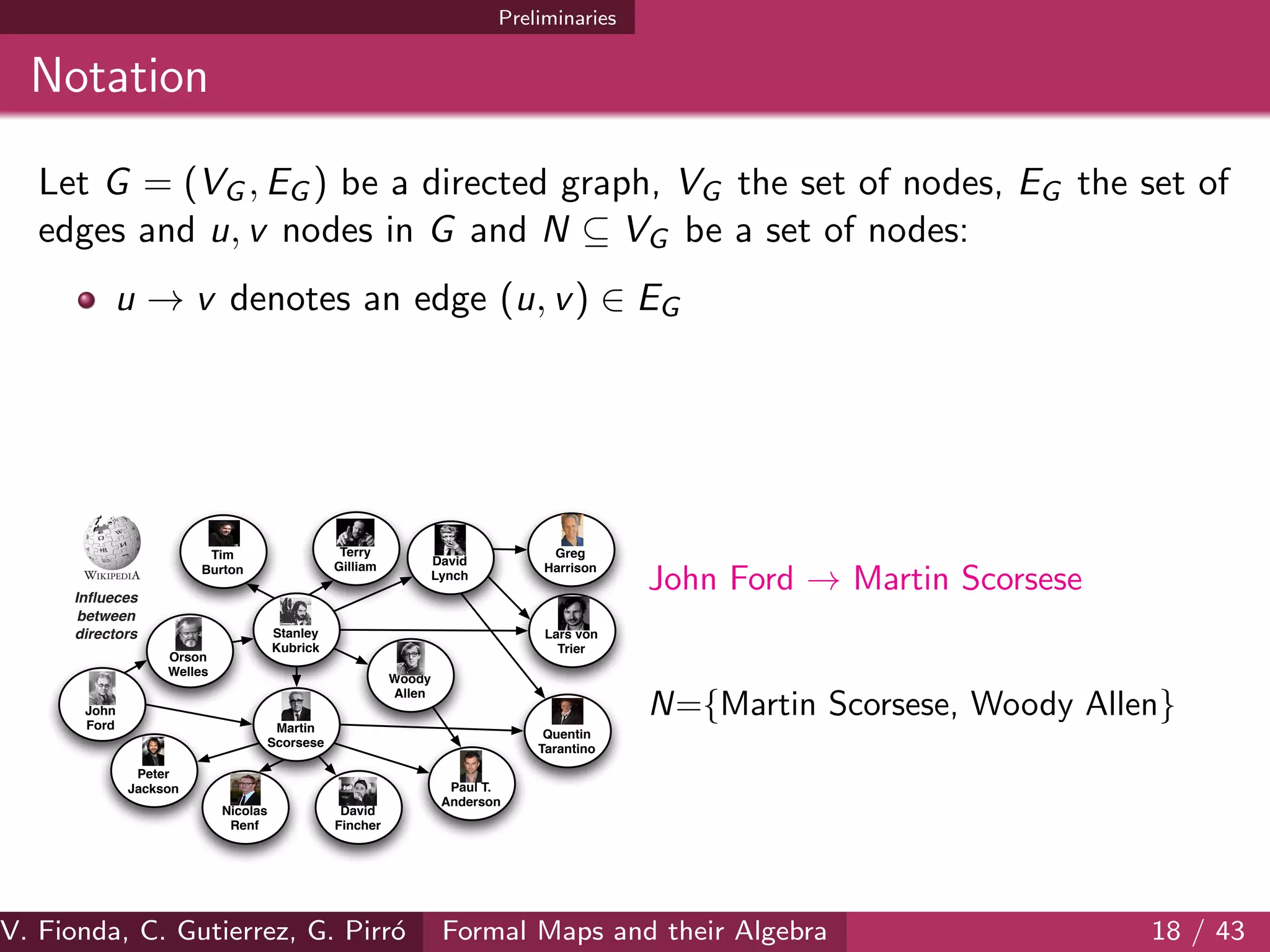
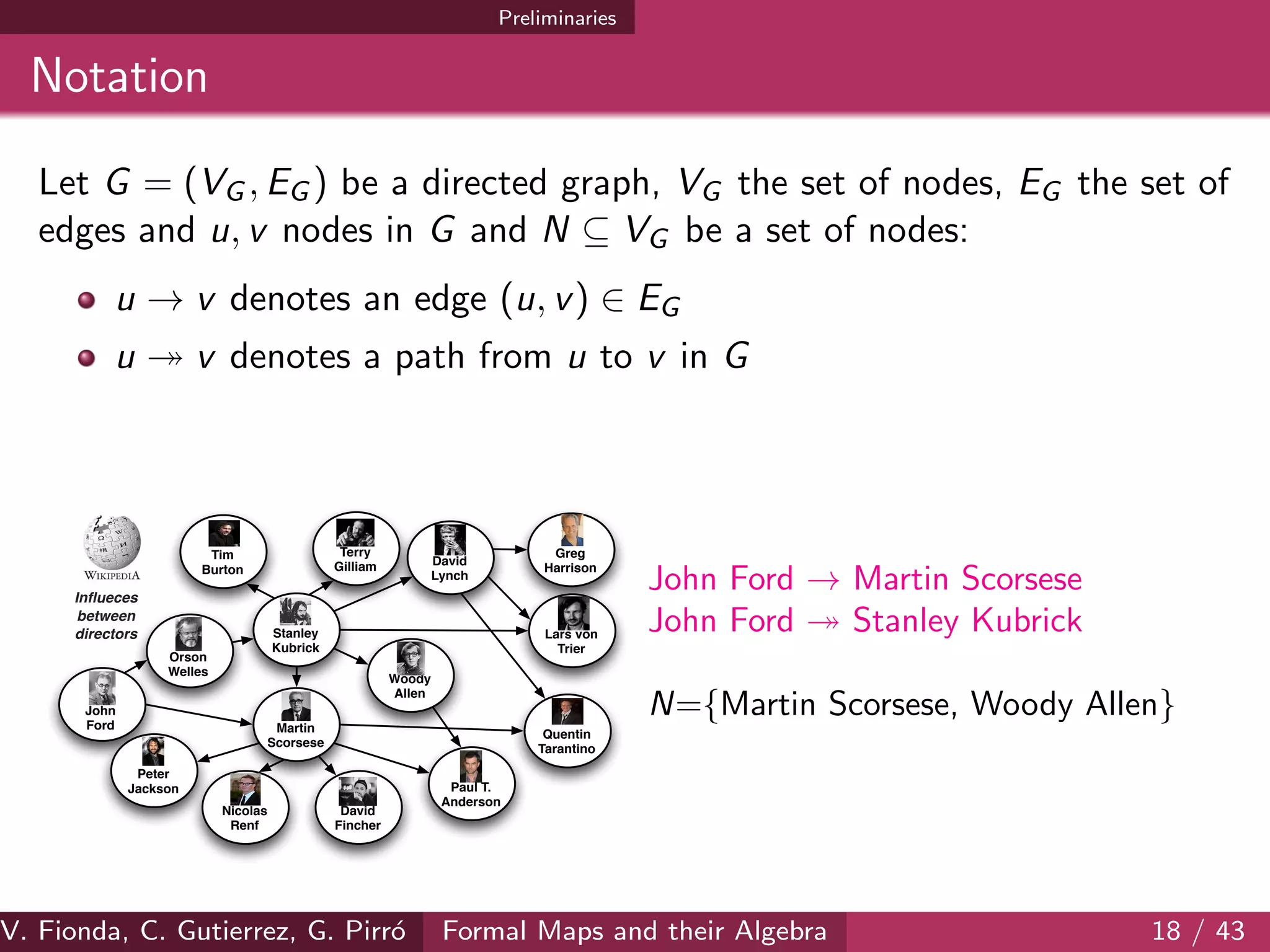
The document discusses formal maps and their algebra, focusing on how cartographical principles can be adapted for web-based applications, particularly in the context of linked data. It outlines contributions made towards providing a general framework for maps as abstractions of graphs, developing algorithms for different map types, and establishing an algebra for maps. The document also addresses challenges and methods for applying these frameworks to web navigation and representation.





















![Related research
Graph summarization
Graph summarization [1,2,3]:
Goal: produce a compressed representation of an input graph G
Determine a function F in order to find a simplified structure Gs
satisfying some requirements
Removes some of the details from the graphs in order to reduce space
consumption by usually clustering nodes in partitions.
[1] C. Faloutsos, K.S. McCurley, and A. Tomkins. Fast Discovery of Connection Subgraphs. In
KDD, pages 118-127. ACM, 2004.
[2] J. Adibi, H. Chalupsky, E. Melz, A. Valente, et al. The KOJAK Group Finder: Connecting
the Dots via Integrated Knowledge-based and Statistical Reasoning. In AAAI, pages 800-807,
2004.
[3] F. Zhou, S. Malher, and H. Toivonen. Network Simplification with Minimal Loss of
Connectivity. In ICDM, pages 659-668. IEEE, 2010.
V. Fionda, C. Gutierrez, G. Pirr´o Formal Maps and their Algebra 14 / 43](https://image.slidesharecdn.com/mapsslides-150605201225-lva1-app6891/75/Formal-Maps-and-their-Algebra-32-2048.jpg)
![Related research
Graph indexing
Graph indexing [4]:
Goal: produce a list of graph substructures with references to the
place where they can be found
Make querying the graph faster
[4] X. Yan and J. Han. Graph Indexing. Managing and Mining Graph Data 2010, pages 161-180
V. Fionda, C. Gutierrez, G. Pirr´o Formal Maps and their Algebra 15 / 43](https://image.slidesharecdn.com/mapsslides-150605201225-lva1-app6891/75/Formal-Maps-and-their-Algebra-33-2048.jpg)













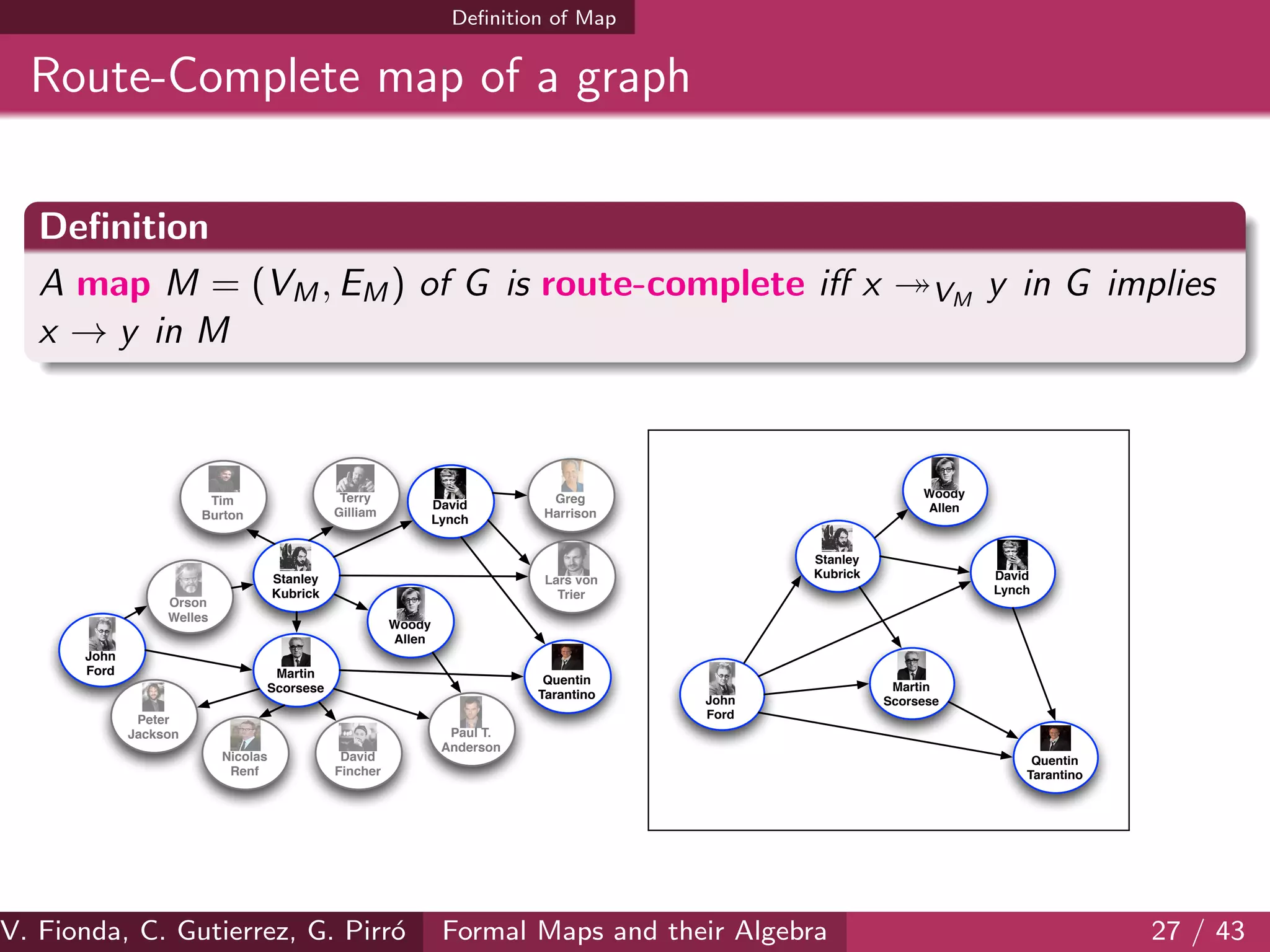

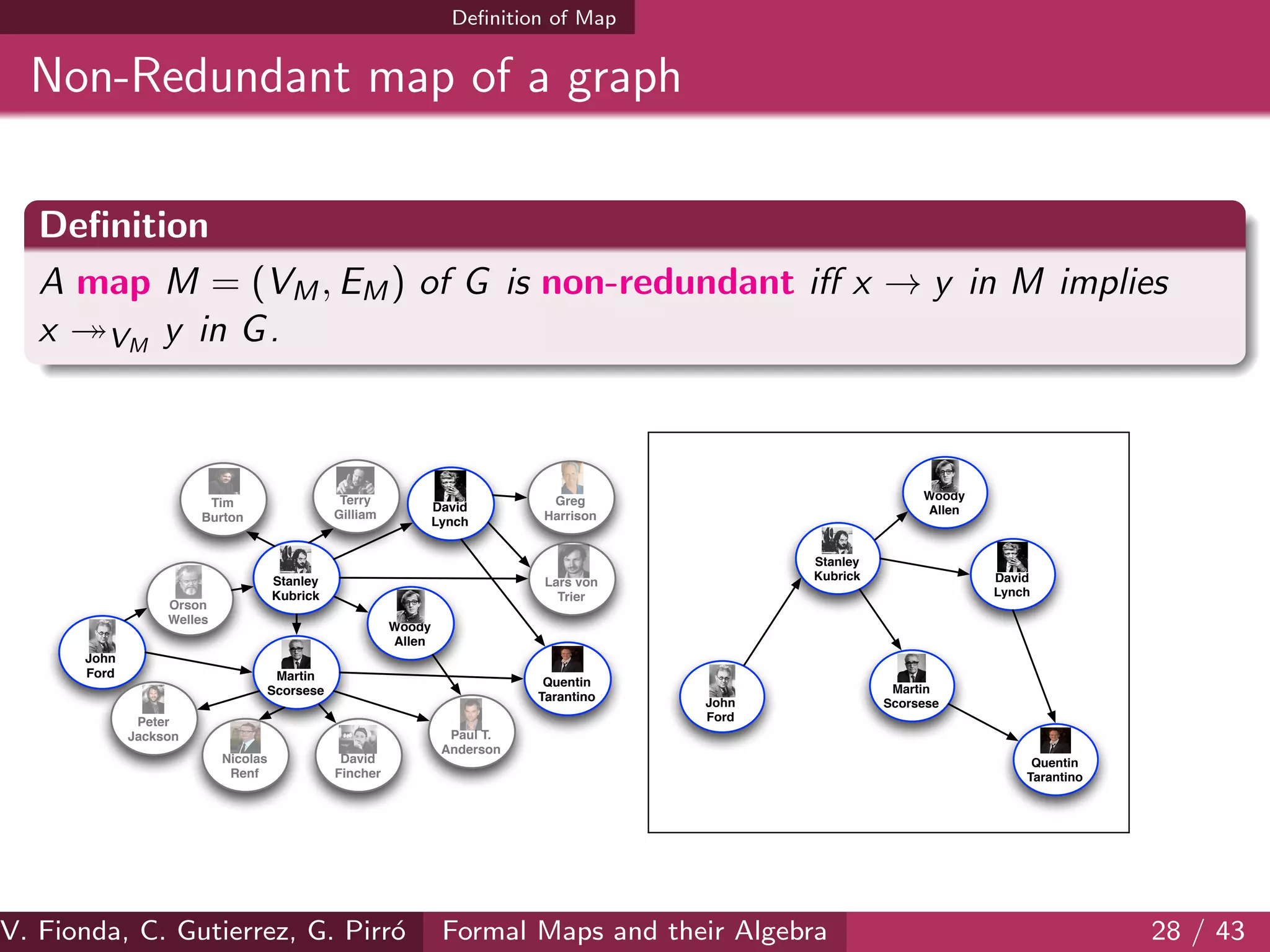

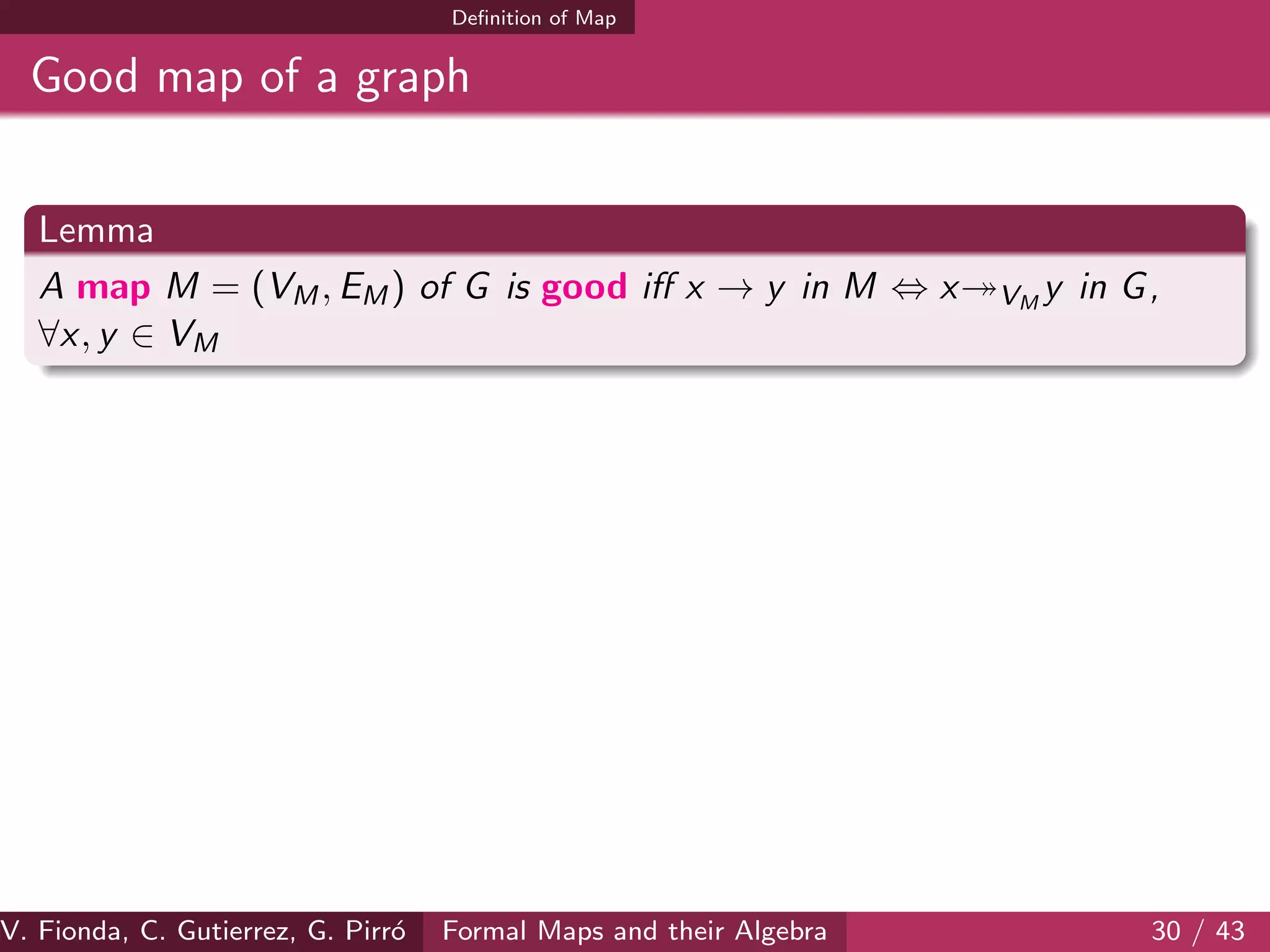



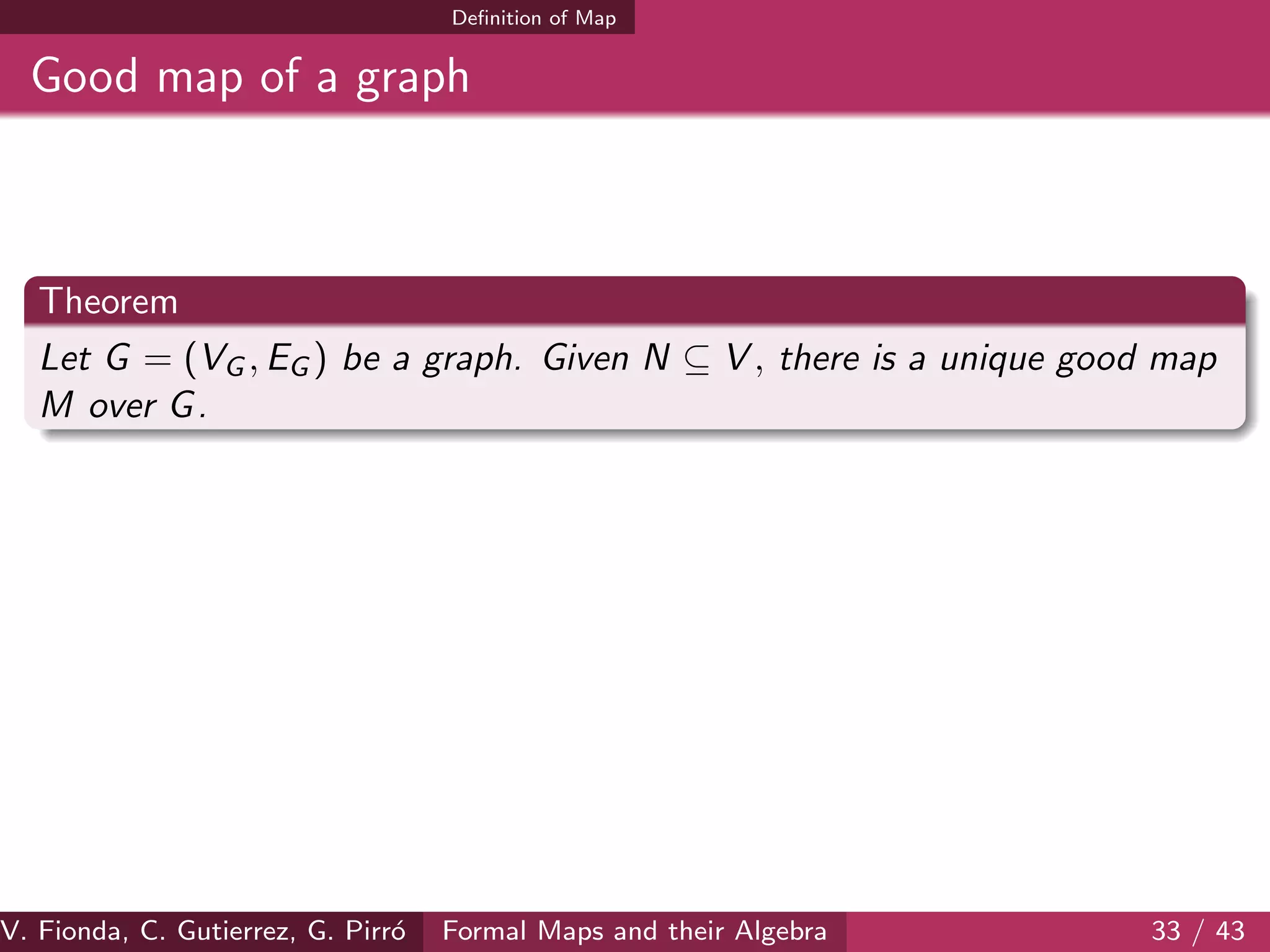





![Regions and maps on the Web
Navigational language to specify regions
Navigational languages [5,6,7] declaratively specify nodes in a graph
or sub-graph (possibly the Web).
No information about node connection is provided and then they are
not suitable for building maps.
We defined a general navigational language to deal with subgraphs
besides sets of nodes.
[5] W. W. W. Consortium. XML Path Language (Xpath) Recommendation., Nov. 1999.
[6] V. Fionda, C. Gutierrez, and G. Pirr´o. Semantic Navigation on the Web of Data:
Specification of Routes, Web Fragments and Actions. In WWW, pages 281290. ACM, 2012.
[7] F. Alkhateeb, J.-F. Baget, and J. Euzenat. Extending SPARQL with Regular Expression
Patterns (for querying RDF). JWS, 7(2):5773, 2009.
V. Fionda, C. Gutierrez, G. Pirr´o Formal Maps and their Algebra 40 / 43](https://image.slidesharecdn.com/mapsslides-150605201225-lva1-app6891/75/Formal-Maps-and-their-Algebra-69-2048.jpg)




