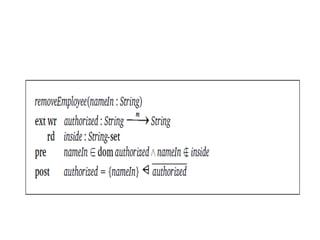
This document introduces maps and their notation. A map relates elements from one set to another, with the first set called the domain and the second called the range. The document defines map notation using examples and discusses various map operators like union, override, domain restriction, range restriction, and their applications. It also provides an example of specifying security access for a high security building using maps and shows a UML diagram.

1. Chapter 11
MAPS

2. Introduction
• Computing systems often involve relating two
types of value together. In Chapter 3 you were
introduced to the idea of a function; you saw that
a function is a set of assignments from one set to
another. A map is closely related to the concept
of functions. A map is a special sort of set, one
which contains a set of maplets. Each maplet
connects an element of one set to an element of
another set; the first set is referred to as the
domain, the second is referred to as the range.

3. Notation
• Consider Table 11.1, which shows the state of
a number of different temperature sensors
that monitor the condition of various items in
a laboratory. The condition of each item can
be either LOW, NORMAL or HIGH.

4. Notation
• We can express the Table 11.1 as a map,
which we might call sensors. This will be a
mapping from a set of sensors to the set of
possible conditions. We do this as follows.
– sensors = {A ↦ LOW, B ↦ NORMAL, C ↦ NORMAL, D ↦
HIGH, E ↦ NORMAL, F ↦ NORMAL}
• In general terms
– m = {a ↦ y, b ↦ x, c ↦ x, d ↦ z}

5. Notation
• Two important points should be noted here:
• By definition, all the domain elements in a
map are unique.
• The ordering of the maplets is not significant –
the map m above could be specified, without
changing the meaning, as:
– m = {d ↦ z, a ↦ y, c ↦ x, b ↦ x}
• You should also note that the empty map is
written as: {↦}.

6. Map Operators
• In order to illustrate the use of the various
map operators that exist, we will define the
following three maps, all of which map from
some previously defined set (the members of
which are represented here by lower case
letters) to the set of natural numbers.
– m1 = {a ↦ 1, b ↦ 2, c ↦ 2, d ↦ 3, e ↦ 4}
– m2 = {a ↦ 2, f ↦ 1, c ↦ 7}
– m3 = { f ↦ 2, g ↦ 6}

7. Domain and Range operators
• The domain operator, dom, returns the set of
all the domain elements of the maplets. The
range operator, rng, returns the set of all the
range elements.
– dom m1 = {a, b, c, d, e}
– rng m1 = {1, 2, 3, 4 }
– dom m2 = {a, f, c}
– rng m2 = {1, 2, 7}

8. The Union operator
• The union operator, U, behaves in a similar way
as it does with sets. So
– m1 U m3 = {a ↦ 1, b ↦ 2, c ↦ 2, d ↦ 3, e ↦ 4, f ↦ 2, g
↦ 6}
• The union operator is defined only if no two
domain elements are the same; if this is not the
case, then union is undefined (otherwise we
would lose the uniqueness of the keys). Thus the
following two expressions are undefined:
– m1 U m2 ---------undefined
– m2 U m3 ---------undefined

9. The Override operator
• In the case where two or more domain
elements are the same in both maps, we can
use the override operator (†). This behaves in
the same way as the union operator, but if the
domain element of a maplet is the same in
both sets, then the second maplet wins. Thus
– m1 † m2 = {a ↦ 2, b ↦ 2, c ↦ 7, d ↦ 3, e ↦ 4, f ↦
1}
– m3 † m2 = { f ↦ 1, g ↦ 6, a ↦ 2, c ↦ 7}

10. Domain restriction operator
• A domain restriction operator, , is defined
with two operands (parameters). The first is a
set and the second is a map. The result yields
a map that contains only those maplets whose
domain element is in the set. For example
– {a, c, e} ◁ m1 = {a ↦ 1, c ↦ 2, e ↦ 4}
– {e, f } ◁ m2 = {f ↦ 1}
– {} ◁ m3 = {↦}

11. Domain deletion operator
• The domain deletion operator, , behaves in a
similar way, but in this case deletes the maplet
in question:
– {a, c, e} ⩤ m1 = {b ↦ 2, d ↦ 3}
– {e, f} ⩤ m2 = {a ↦ 2, c ↦ 7}
– {} ⩤ m3 = { f ↦ 2, g ↦ 6}

12. Range restriction and range deletion
operator
• The range restriction operator, , and the range
deletion operator, , are similar to the above,
but apply to the last elements of the maplets.
Thus
– m1 ▷ {1, 2} = {a ↦ 1, b ↦ 2, c ↦ 2}
– m3 ⩥ {6, 2} = {↦}

13. Map application
• Applying a map is the same as applying a
function, and we use the same notation. Thus if
we apply our map to a particular domain
element, then the result is the range element. For
example, once again using the above maps:
– m1(d) = 3
– m2( f ) = 1
– m3( f ) = 2
– m3(x) is undefined
• Using the sensors example from section 11.2:
– sensors(A) = LOW

14. Using the Map Type in VDM-SL
• To declare a variable to be of type Map we use
a special arrow. For example, to declare a
variable m that maps characters to natural
numbers we would write:
– m : Char ℕ

15. Specifying a high security building
• Only authorized employees are allowed entry to the
building and each one consists of a user name (which is
unique) and a password, both of which must be
supplied when the individual wishes to enter the
building. If the details are correct, a signal is sent to the
hardware instructing it to open the door, and the
member of staff is recorded as being inside the
building. When the member of staff wishes to leave
the building, the individual supplies his or her user
name, and as long as the user is recorded as being
currently inside the building, a signal is sent to the
hardware to open the door, and the employee is
recorded as having left.

16. UML Diagram

26. Thanks