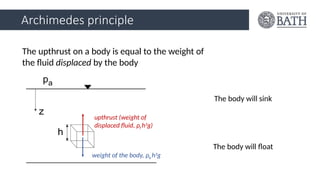
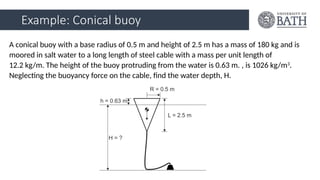
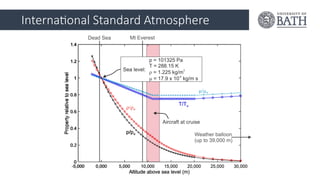
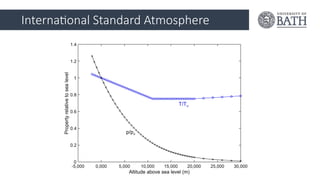
Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1 Flui Lecture 1