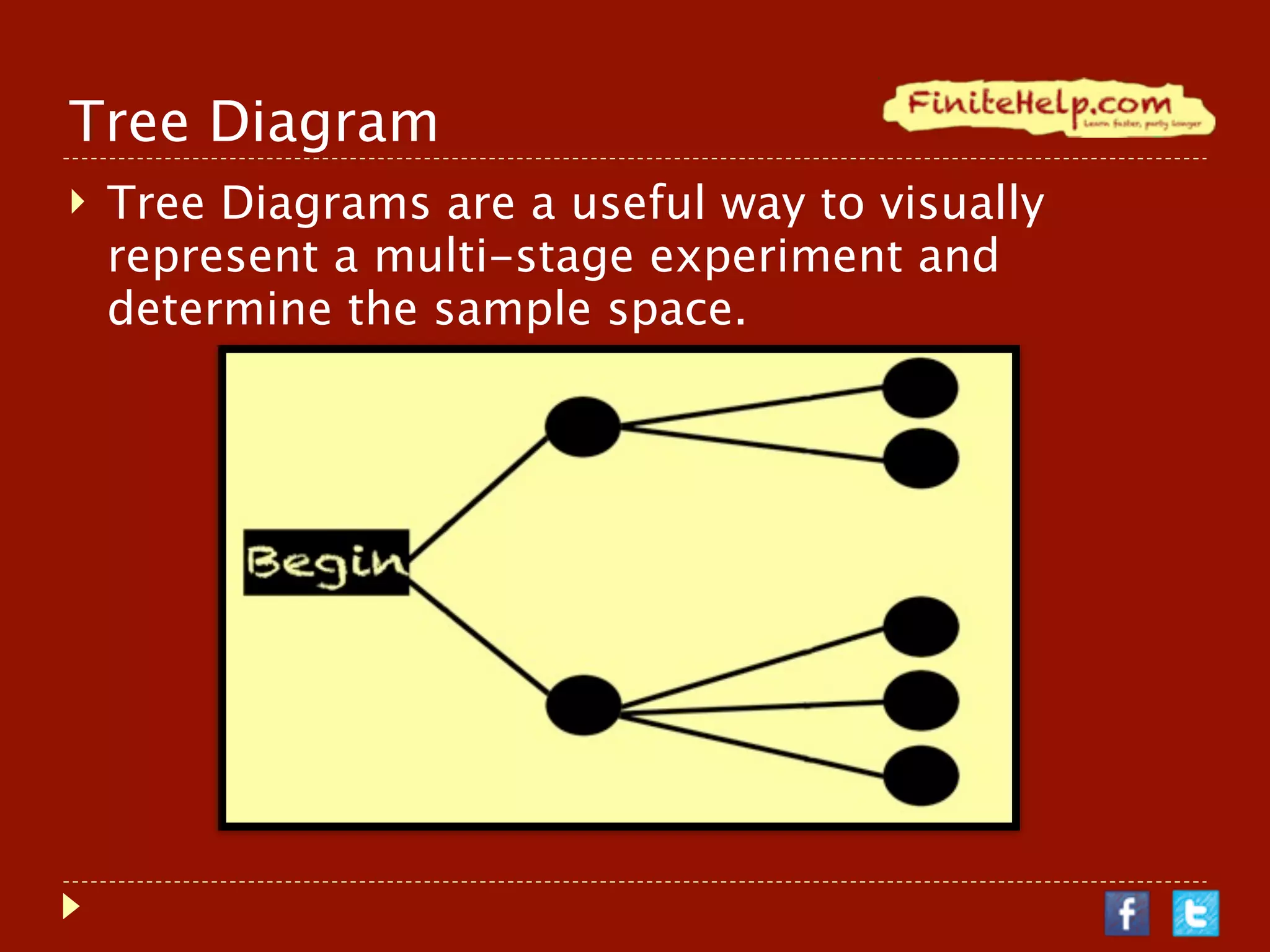
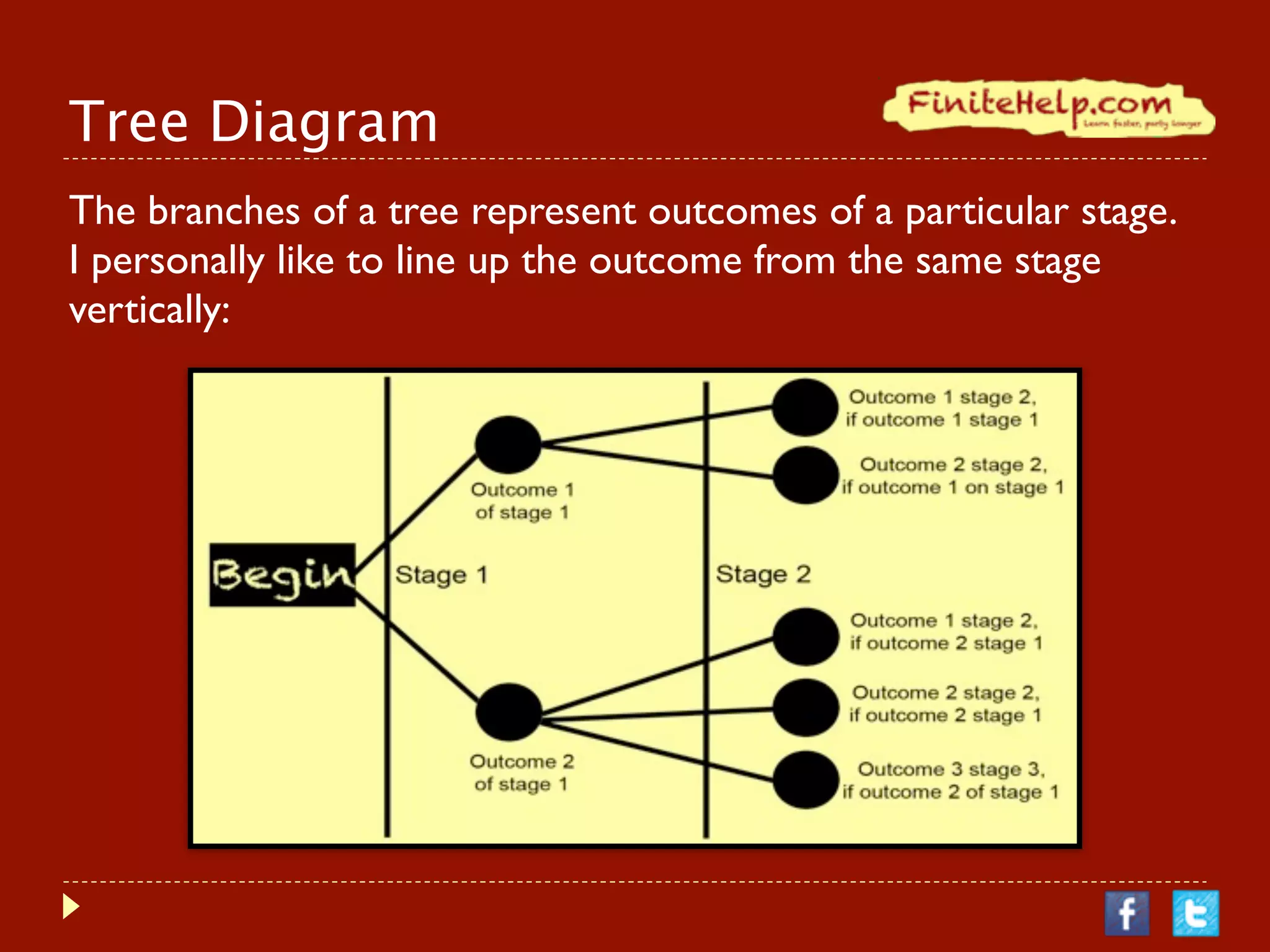
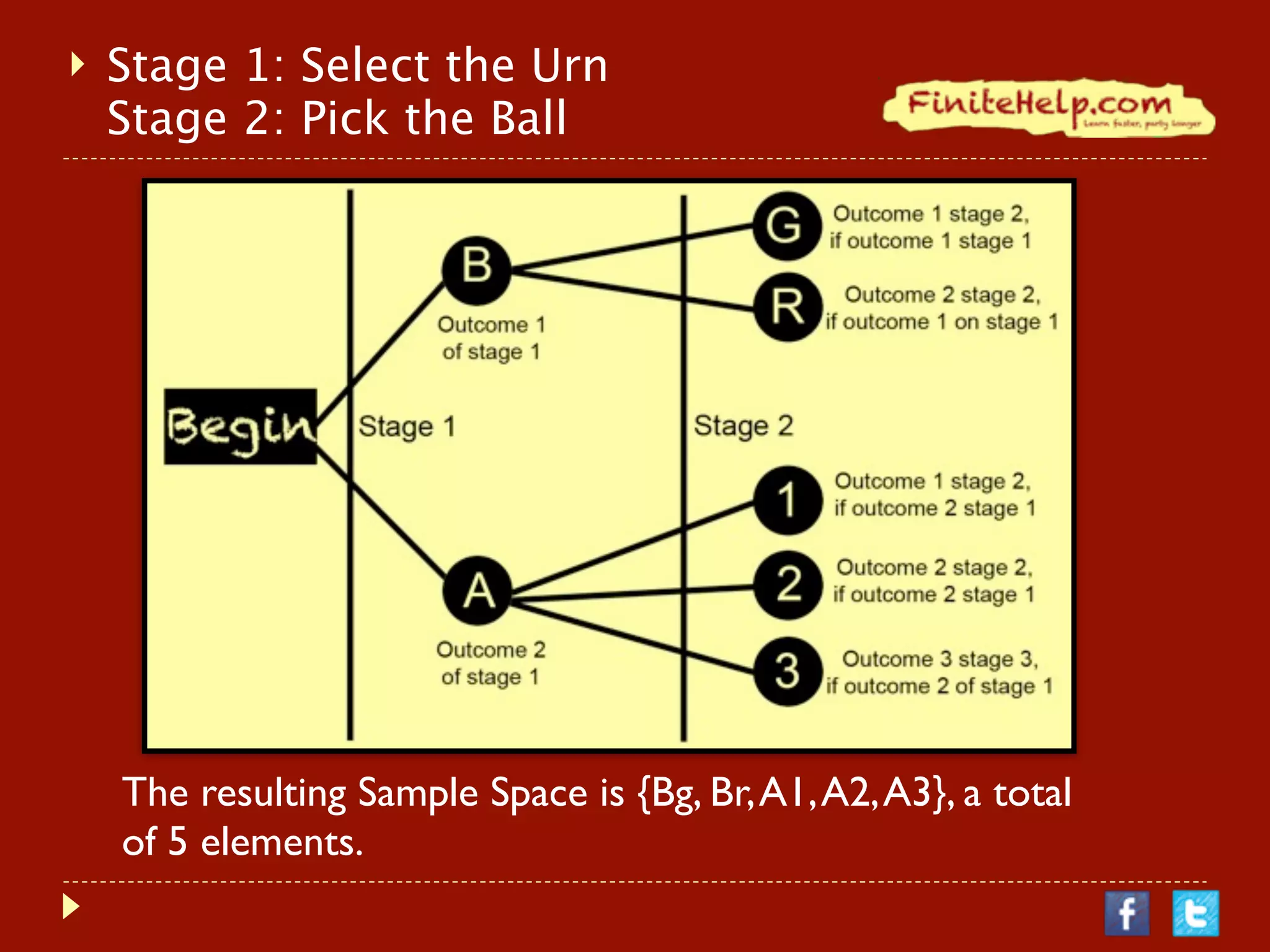
The document explains the concepts of random experiments, sample spaces, and tree diagrams, illustrating these ideas with examples and quizzes. It also covers the multiplication principle for calculating the number of outcomes in multi-stage experiments. Additionally, it promotes resources for further learning, including recorded lectures and practice problems.

1. 1.4
Sets of Outcomes and Trees

2. Random Experiment
and Sample Space
 A random experiment is an experiment with
multiple possible outcomes.
Ex: Rolling a die, flipping a coin
 A “sample space” is the set of collection of all
those outcomes.
Ex: For experiment of “rolling a dice”,
SS = {1, 2, 3, 4, 5, 6}

3. Tree Diagram
 Tree Diagrams are a useful way to visually
represent a multi-stage experiment and
determine the sample space.

4. How to
make a Tree Diagram
 Let use this following experiment as the example for
our tree:
“There is Urn A and Urn B. Urn A has balls
numbered 1, 2, 3. Urn B has balls colored green and
red. You choose an urn and draw a ball from it.”
A B

5. Tree Diagram
The branches of a tree represent outcomes of a particular stage.
I personally like to line up the outcome from the same stage
vertically:

6.  Stage 1: Select the Urn
Stage 2: Pick the Ball
The resulting Sample Space is {Bg, Br, A1, A2, A3}, a total of 5 elements.

7. Representing an outcome twice
 A common mistake many students make is to put
down a repeated outcome multiple times. Let’s say
there are 2 green balls in urn B. You would still only
have one branch representing both green balls.
Making two separate branches for one outcome is
incorrect:
B

8. Quiz 1.4.1

9. Quiz 1.4.1
 Consider the following experiment: Fred goes to
dinner and have to pay the bill, which comes to
$7. He has one $10, one $5, and three $1. He
pull random bills out of the pocket until he has
enough to pay. How many elements are in the
sample space?
A. 9
B. 10
C. 11

10. Quiz 1.4.1
 Consider the following experiment: Fred goes to
dinner and have to pay the bill, which comes to
$7. He has one $10, one $5, and three $1. He
pull random bills out of the pocket until he has
enough to pay. How many elements are in the
sample space?
A. 9
B. 10
C. 11

11. Quiz 1.4.1
 Consider the following experiment: Fred goes to
dinner and have to pay the bill, which comes to
$7. He has one $10, one $5, and three $1. He
pull random bills out of the pocket until he has
enough to pay. How many elements are in the
sample space?
A. 9
B. 10
C. 11
 Answer: C

12. Multiplication principle
 If you have a multi-stage experiment, with equal number of
possibilities in each stage regardless of the previous stage,
there’s a simple way to calculate the number of element in
sample space.
 For example, Bob goes to McDonald to get a Happy meal. He
can choose cheeseburger, nuggets, or chicken sandwich for
entrée, soft drink, juice or milk for the drink, and 4 different
toys.
 The number of combinations he could get is 3 x 3 x 4 = 36.
(3 entrée, 3 drinks, 4 toys)

13. Quiz 1.4.2
 Mike goes to subway and gets a sandwich. He
can choose between 5 kinds of bread, 4 kinds of
cheese, and 3 kinds of meat. How many
different sandwiches does he have to choose
from?
A. 20
B. 60
C. 120

14. Quiz 1.4.2
 Mike goes to subway and gets a sandwich. He
can choose between 5 kinds of bread, 4 kinds of
cheese, and 3 kinds of meat. How many
different sandwiches does he have to choose
from?
A. 20
B. 60
C. 120
 Answer: B

15. Summary
 Definition:
 Random experiment
 Sample space
 How to make a Tree Diagram
 determine sample space
 Multiplication Principle

16.  Features
 27 Recorded Lectures
 Over 116 practice problems with recorded solutions
 Discussion boards/homework help
 Visit finitehelp.com to find out more
For special offers and additional content...
Follow us on twitter @finitehelp Become a fan on Facebook