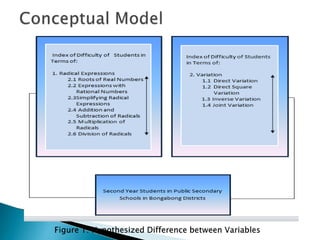
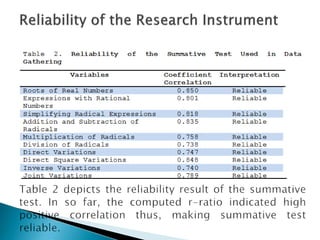
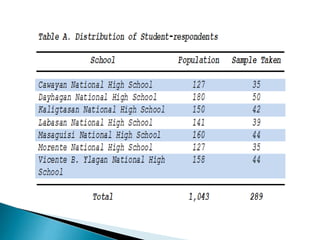
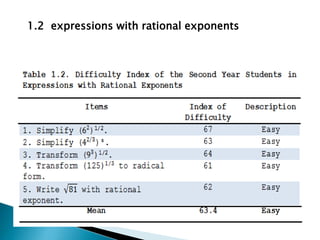
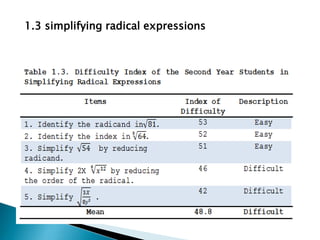
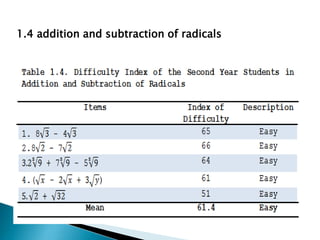
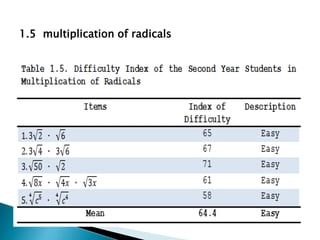
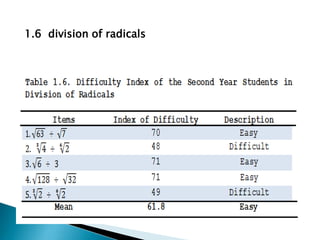
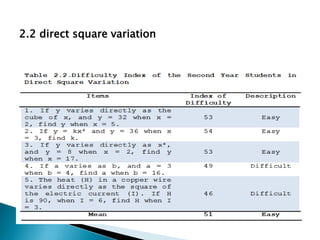
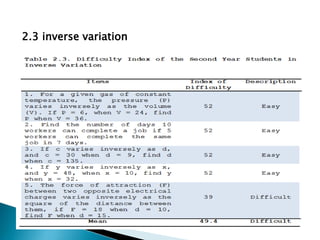
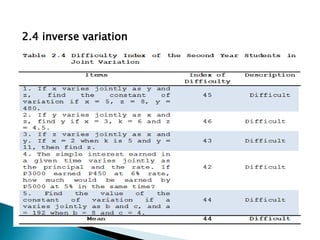
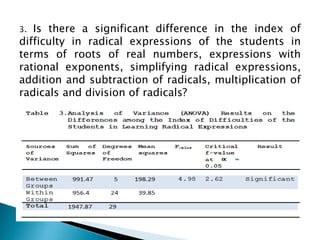
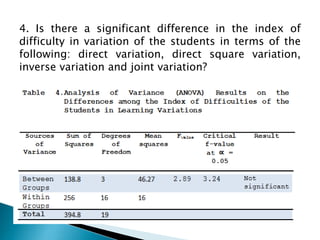
This study examined the difficulties of intermediate algebra students in the Philippines in topics related to radicals and variations. It found that students generally found roots of real numbers, expressions with rational exponents, addition/subtraction of radicals, and multiplication/division of radicals to be easy. However, students found simplifying radical expressions, direct variation, inverse variation, and joint variation to be difficult. The study also found a significant difference in students' difficulties with different radical expression topics, but no significant difference in their difficulties with different variation topics. It recommends providing more practice with simplifying radicals and variations to help students improve in these areas.

2. This study aimed to determine the difficulties in
Intermediate Algebra of Second Year students in public
secondary schools in Bongabong.
Specifically, it sought to answer the following
questions:
1.What is the index of difficulty of the students in
radical expressions in terms of the following:
1.1 roots of real numbers
1.2 expressions with rational exponents
1.3 simplifying radical expressions
1.4 addition and subtraction of radicals
multiplication of radicals
1.6 division of radicals?

3. 2. What is the index of difficulty of the students in
variation in terms of the following:
2.1 direct variation
2.2 direct square variation
2.3 inverse variation
2.4 joint variation?
3. Is there a significant difference in the index of
difficulty in radical expressions of the students in
terms of roots of real numbers, expressions with
rational exponents, simplifying radical expressions,
addition and subtraction of radicals, multiplication of
radicals and division of radicals?
4. Is there a significant difference in the index of
difficulty in variation of the students in terms of the
following: direct variation, direct square variation,
inverse variation and joint variation?

4. 1. There is no significant difference in the index of
difficulty in radical expressions of the students in
terms of roots of real numbers, expressions with
rational
exponents,
simplifying
radical
expressions, addition and subtraction of radicals,
multiplication of radicals and division of radicals.
2. There is no significant difference in the index of
difficulty in variation of the students in terms of
the following: direct variation, direct square
variation, inverse variation and joint variation.

6. The diagram shows the variables in the study
which include the index of difficulty of Second Year
Students in Public Secondary Schools in Bongabong
Districts in terms of: radicals –roots of real
numbers, expressions with rational numbers,
simplifying radical expressions, addition and
subtraction of radicals, multiplication of radicals
and division of radicals; and variation– direct
variation, direct square variation, inverse variation
and joint variation.
The
two-headed
arrow
signifies
the
hypothesized differences among the index of
difficulty in the indicators of radical expressions
and variations.

8. To determine the index of difficulty of
each item, the majority criterion (50 percent
plus one) was used as basis to describe the
Means.
Range
51% - 100%
50%
1% - 49%
Description
Easy (E)
Neither Easy nor Difficult (N)
Difficult (D)

12. 1. What is the index of difficulty of the students
in radical expressions in terms of the following:
1.1 roots of real numbers

13. 1.2 expressions with rational exponents

14. 1.3 simplifying radical expressions

15. 1.4 addition and subtraction of radicals

16. 1.5 multiplication of radicals

17. 1.6 division of radicals

18. 2. What is the index of difficulty of the students
in variation in terms of the following:
2.1 direct variation

19. 2.2 direct square variation

20. 2.3 inverse variation

21. 2.4 inverse variation

22. Is there a significant difference in the index of
difficulty in radical expressions of the students in
terms of roots of real numbers, expressions with
rational exponents, simplifying radical expressions,
addition and subtraction of radicals, multiplication of
radicals and division of radicals?
3.

23. 4. Is there a significant difference in the index of
difficulty in variation of the students in terms of the
following: direct variation, direct square variation,
inverse variation and joint variation?

24. This chapter presents the summary of the
findings, conclusions and recommendations.

25. 1. What is the index of difficulty of the students in radical
expressions terms of the following:
1.1 Roots of real numbers. This topic has a mean index of
difficulty of 66.6, described as easy.
1.2 Expressions with rational exponents. The items under
this topic have a mean index of difficulty of 63.4 described
as easy.
1.3 Simplifying radical expressions. Items under this topic
have a mean difficulty index of 48.8 described as difficult.
1.4 Addition and subtraction of radicals. This topic has an
overall mean index of difficulty 61.4 described as easy.
1.5 Multiplication of radicals. All items on multiplication of
radicals has a mean index of difficulty 64.4 described as
easy.
1.6 Division of radicals. This topic has an overall mean
index of difficulty 61.8 described as easy.

26. 2. What is the index of difficulty of the
students in variation terms of the following:
2.1 Direct variation. The mean index of
difficulty of these items is 49.2 described as
difficult.
2.2 Direct square variation. The items have a
mean difficulty index of 51 described as easy.
2.3 Inverse variation. The mean index of
difficulty for inverse variation is 49.4
described as difficult.
2.4 Joint variation. The mean difficulty index
of the items is 44 described as difficult.

27. 3. Is there a significant difference in the index of difficulty of
the students in terms of radical expressions?
The computed F-value of 4.98 was greater than the
critical f-value of 2.62 using 5 and 24 degrees of freedom
at 5% level of significance. Therefore, the null hypothesis
was rejected.
This means pupil respondents have
varied index of difficulty in learning radical expressions.
4. Is there a significant difference in the index of difficulty of
the students in terms of variation?
The computed value of 2.89 was lower than the critical
value of 3.24 using 3 and 16 degrees of freedom at 5%
level of significance. Thus, the null hypothesis was
accepted. There is no significant difference in the index of
difficulty of the students in terms of variation. This means
they encountered similar difficulties in answering the
items on variations.

28. Based on the findings of the study, the study concluded the following:
1. The study revealed that the students found roots of real numbers
easy.
2. The results also showed that expressions with rational exponents
were easy for the students.
3. Simplifying radical expressions is difficult for the students.
4. The results suggested that addition and subtraction of radicals is easy
for the students.
5. Multiplication of radicals was found out easy by the students.
6. Division of radicals was easy for the students.
7. Direct variation is difficult for the students.
8. The items for direct square variation were easy for the students.
9. Inverse variation was difficult for the students.
10. Solving joint variation was difficult for the student-respondents.
11. The index of difficulty of the students in radical expressions varies
significantly.
12. The index of difficulty of the students in variation does not vary.

29. Based on the findings and conclusions, the researcher arrived at
the following recommendations:
1. Mathematics teacher should continue using their strategies in
teaching roots of real numbers.
2. The teacher should continuously give emphasis on exponents
when teaching radical expressions with radical exponents.
3. Factoring should be given attention when teaching simplifying
radical expressions.
4. Constant drills and exercises in addition, subtraction,
multiplication and division should be done to further enhance
these skills; thus, making solving easy for the students.
5. Comprehension skills, clear understanding of direct
relationship between quantities, skills to represent and operate
the unknown, analysis and problem solving skills should be
developed to make problem-solving easy for the students.
6. Future research related to this study should be conducted to
generalize the findings of this study.

30. THANK
YOU SO
MUCH
!!!!! &
GOD
BLESS
US
ALL…..