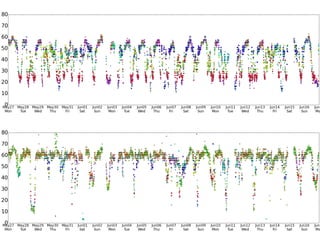
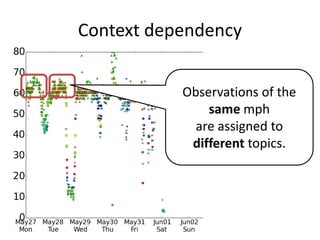
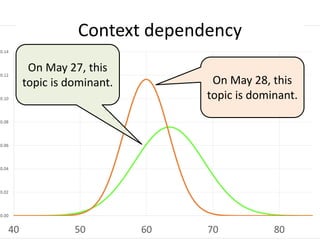
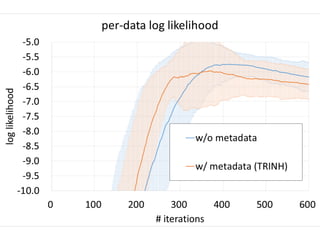
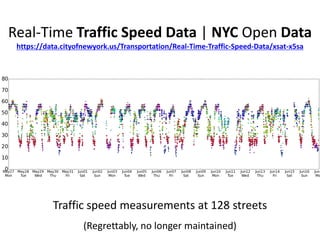
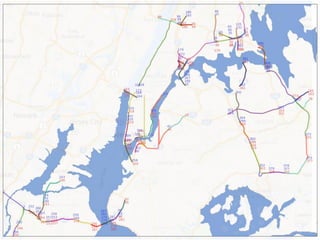
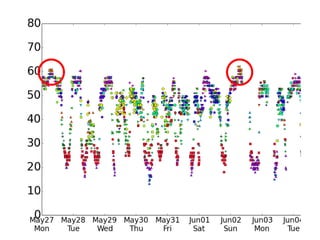
This document summarizes a hierarchical topic modeling approach for analyzing traffic speed data. The model treats each day's data as a mixture of different speed distributions. It extends latent Dirichlet allocation to model speeds as continuous gamma distributions rather than discrete words. The model further incorporates metadata on time of day and sensor location to make topic probabilities dependent on context. Model parameters are estimated using variational Bayesian inference, and the model achieves better performance than alternatives by capturing similarity between observations based on timing and location.

1. Traffic Speed Data Investigation
with
Hierarchical Modeling
Tomonari MASADA
Nagasaki University
masada@nagasaki-u.ac.jp

2. Real-Time Traffic Speed Data | NYC Open Data
https://data.cityofnewyork.us/Transportation/Real-Time-Traffic-Speed-Data/xsat-x5sa
Traffic speed measurements at 128 streets
(Regrettably, no longer maintained)

5. Problem 1
• Traffic speed data show a clear
periodicity at one day period.
• However, many different traffic speed
distribution patterns can be observed
also within each period.

6. Solution 1 [Masada+ 14]
• We take intuition from topic models
in text mining.
–The data set of each day should be
modeled as a mixture of many
different speed distributions.

7. Latent Dirichlet Allocation (LDA) [Blei+ 03]
• LDA achieves a word token level clustering.
• Not a document level clustering
• Each document is modeled as a mixture of
many different word probability distributions.
topic <-> word probability distribution
document <-> topic probability distribution

8. v3
v1
v3
v2
v2
v1 v2 v3 v4
t3
φ31
φ32
φ33
φ34
v1 v2 v3 v4
t2φ21
φ22
φ23
φ24
v1 v2 v3 v4
t1
φ11
φ12
φ13
φ14
θj1 θj2
θj3

9. An important difference
• Words are discrete entities.
– LDA uses multinomial distribution for modeling
per-topic word distribution.
• Speeds (in mph) are continuous entities.
– Our model uses gamma distribution.

10. gamma distribution

11. Comparison with LDA
• word token
<-> speed measurement (in mph)
• topic (multinomial)
<-> topic (gamma)
• document
<-> document (24 hrs from midnight)

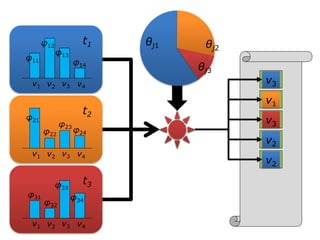
12. Full joint distribution
• We estimated parameters by a variational
Bayesian inference. [Masada+ 14]

13. Problem 2
• Traffic speed data may show a similarity
at the same time point of day.
• Traffic speed data may show a similarity
for the streets whose locations are close
to one another.

14. Solution 2 [Masada+ FDSE15]
• We use metadata in topic models.
–time points
–geographic locations

15. TRINH = TRaffic speed INvestigation
with Hierarchical modeling
• Make topic probabilities dependent on
time points and on locations
– probability that the speed measured by the sensor
s at the time point t is assigned to the topic k
𝜃 𝑑𝑡𝑘 ≡
exp(𝑚 𝑑𝑘 + 𝜆 𝑘𝑠 + 𝜏 𝑘𝑡)
𝑘′ exp(𝑚 𝑑𝑘′ + 𝜆 𝑘′ 𝑠 + 𝜏 𝑘′ 𝑡)

16. Parameters
• 𝑚 𝑑𝑘
– How often the document d provides the topic k
• 𝜆 𝑘𝑠
– How often the sensor s provides the topic k
• 𝜏 𝑘𝑡
– How often the time point t (of day) provides the
topic k

17. Priors for parameters ("hierarchical")
• 𝑚 𝑑𝑘
–K Gaussian priors
• 𝜆 𝑘𝑠
–K Gaussian process priors
• 𝜏 𝑘𝑡
–K Gaussian process priors

18. Full joint distribution

19. Inference by MCMC
• Sample from the posterior distribution
–Slice sampling for topic probability
parameters 𝑚 𝑑𝑘, 𝜆 𝑘𝑠, and 𝜏 𝑘𝑡
–Metropolis-Hastings for hyperparameters

21. Context dependency
Observations of the
same mph
are assigned to
different topics.

22. Context dependency
On May 27, this
topic is dominant. On May 28, this
topic is dominant.

23. Comparison experiment
• Log likelihood per measurement
–Larger is better.
• Data
–May 27 ~ June 16, 2013 (three weeks)
• Data files were downloaded every minute.
–20% measurements for testing

25. Prior as regularization
Too strong?

26. What we achieved
• We obtained an MCMC for a topic model
whose topic probabilities are defined by
combining multiple factors.
• And the factors are correlated via Gaussian.
– Our model can also be applied to other types of
metadata indicating intrinsic similarity of data.

27. Summary
• We proposed a topic model for traffic data analysis.
• Sensor locations and measurement timestamps
affects topic assignment.
• TRINH achieves better likelihood in earlier iterations.
• However, TRINH gives worse likelihood in later
iterations.

28. Future work
• Control the strength of regularization
– e.g. by weighting the factors.
𝜃 𝑑𝑡𝑘 ≡
exp(𝑚 𝑑𝑘 + 𝜆 𝑘𝑠 + 𝜏 𝑘𝑡)
𝑘′ exp(𝑚 𝑑𝑘′ + 𝜆 𝑘′ 𝑠 + 𝜏 𝑘′ 𝑡)
• Look for other data sets
– Location information should be more relevant.