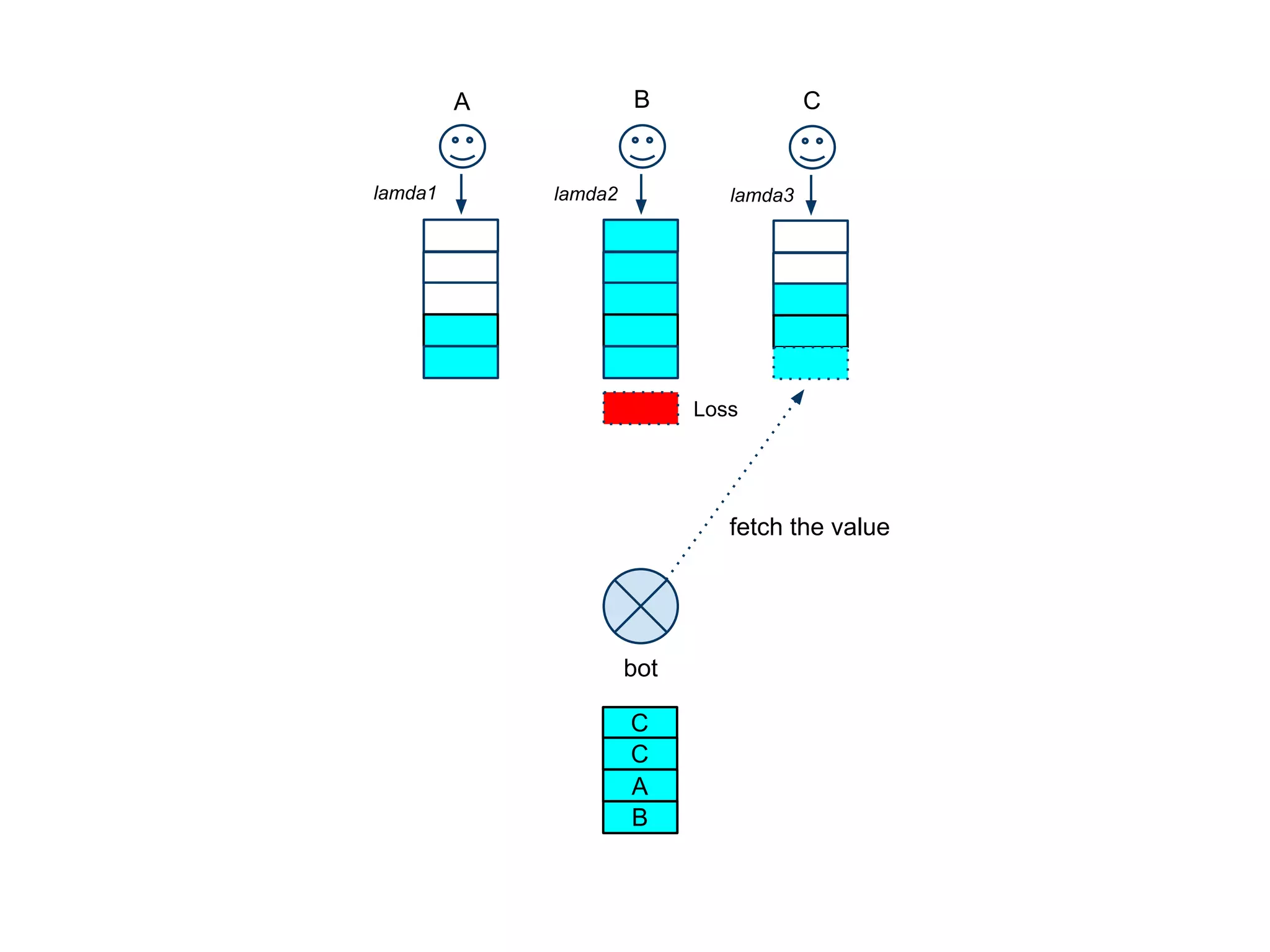
The document proposes an efficient scheme to monitor multiple queues with limited resources by modeling human behavior. It suggests distributing monitoring requests to queues based on the activity level of the users generating content for each queue. The inter-event times between tasks in each queue are modeled as following a power-law distribution based on empirical evidence. An experiment is described to generate inter-event times for each queue based on the distribution and fit within the total monitoring time available.

1. Efficient queue monitoring scheme
based on human behavior
Jae Sohn (arisohn@gmail.com)

2. Problem definition :
Which scheme is efficient(minimize loss of information) to monitor
every queue with restricted resource when N-person produce
information to own fixed length queue? (restricted resource: the
number of queue monitoring per hour)
N명의 사람이 각자의 큐(고정된 크기)에 정보를 만들때, 제한된 자
원하에서 어떻게 모든 큐를 모니터링 하는것이 효율적(손실되는 정
보양을 최소화)인것인가? (제한된 자원: 시간당 큐를 모니터링 할
수 있는 횟수)

3. Loss
bot
fetch the value
lamda1 lamda2 lamda3
A B C
C
C
A
B

4. Job Distribution Strategy
● Limited number of requests.
● Suitable number of requests must be distributed to each one
● Higher active user, more frequent requests are distributed
● Who is an active user?
○ Activity measure ( T. Zhou, H.A.T. Kiet, B.J. Kim, B.-H. Wang, and P. Holme , Role of Activity in Human
Dynamics , EPL 82, 28002 (2008) )
○ A ( activity ) = n/T where n is the number of events and T time interval between start and end time

5. Human behavior on inter-event time
● Individual executes at first a task with highest priority in the queue
● The distribution of the inter-event time(waiting time) between two consecutive tasks is
power-law( A. L. Barabasi, Nature 435, 207(2005), A. Vazquez, Exact results for the Barabasi model of human
dynamics, Phys. Rev. Lett. 95, 248701 (2005) )
● In many literatures, the Barabasi model is confirmed empirically
○ waiting time distribution( waiting time defined by time interval between a task arrival time on the
queue and execution time( leave a queue) ) has power law.
■ finite queue length: exponent ~ 3/2 : surface mail based on correspond
■ infinite queue length: exponent ~ 1 : web browsing, email, library visitation
○ task arrival rate(lambda) and execution rate(mu)
○ inter-event time

6. Modelling and Experiment
● Choose N-users with meaningful number of contents
● Grouping users with activity ( e.g. A = 0~0.1, ~0.2, ~0.3, ... )
● Given possible total requests(R), distribute requests(R_i) to each user. The
number of requests(R_i) distributed to each user depend on user's activity
(A_i).
● Find the inter-event time distribution of each user( p(tau)~tau-alpla
) by a
fitting
● construct p-1
(tau)
● In T, time interval between experiment start time and end time, generate R_i
requests. Then, the number of taus( inter-event time) for i-user is R_i.
Therefore, the sum of taus must be T. One need to scale the p-1
(tau) or
each tau-value.

7. p-1
(tau) construction
● time interval T between experiment start time and end time
● request number : r
● inter-event time : tau(1), tau(2), ...., tau(r)
● Method
○ set taumin
, taumax
( taumin
~0, taumax
~ T )
○ for( i= 1; i<r ; i++ )
■ tau(i) = p-1
(tau) 0 < tau < T(i)
■ T(i) = T(i) - tau(i)
○ i=r
■ tau(r) = p-1(tau) 0 < tau < T(r-1) or tar(r) = T(r-1)