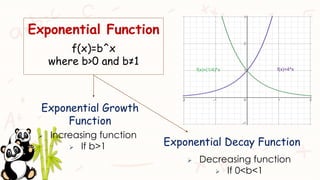
The document discusses exponential growth and decay functions. It provides examples of using exponential functions to model simple interest, compound interest, and population decay. The examples are solved step-by-step and the answers are provided in complete sentences. Various formulas are presented for exponential growth, decay, simple interest, and compound interest.

1. EXPONENTIAL
MODELS
Jessica Marie Aguirre
11-St. Pedro Calungsod

2. INTRODUCTION

3. Exponential Growth
Function
Exponential Decay Function
➢ Decreasing function
➢ If 0<b<1
f(x)=4^x
f(x)=(1/4)^x
f(x)=b^x
where b>0 and b≠1
Exponential Function
➢ Increasing function
➢ If b>1

4. EXPONENTIAL
Growth Function
S
I
M
P
L
E
I
N
T
E
R
E
S
T

5. Exponential Growth Function
(Simple Interest)
Tom operates a fast-food restaurant that earns ₱ 75 000.00. If his income’s
rate of increase is 8% annually, how much will he earn after 7 years?
Given:
a (starting number)- ₱
75,000.00
Percent
Increase/Rate- 8%
b (growth factor)-
100%+8%=108%= 1.08
x (intervals, in years)=
7
Looking for:
y (earnings after 7
years, in pesos)
Formula:
y= a · 𝑏𝑥
Solving:
y= 75,000 · (1.08) ^7
y= 75,000 · (1.71382427)
y=128536.82
Answer:
₱ 128,536.82
Answer in a sentence:
Tom will earn ₱ 128,536.82
from his fast-food restaurant
after 7 years.

6. EXPONENTIAL
Growth Function
C
O
M
P
O
U
N
D
I
N
T
E
R
E
S
T

7. Exponential Growth Function
(Compound Interest)
Margarette invested ₱ 40,000.00 at an annual rate of 3% compounded
quarterly. Find the total amount of money in her account after 9 years
considering no withdrawals or additional deposits are made.
Given:
P- ₱ 40,000.00
r- 0.03 (3%)
n-
1
4
(quarterly)
t- 9 years
Solving:
A= 40 ,000(1+
0.03
4
)9
A= 40 ,000(1.0075)9
A= 40,000 (1.06956084 )
A= ₱ 42,782.4336
Final answer:
There would be ₱ 42,782.43
in Margarette’s account after 9 years.
Looking for:
A- Compound amount
in 9 years
Formula:
A= P(1+
𝑟
𝑛
)𝑡
Compound value:
A= ₱ 42,782.43

8. EXPONENTIAL
Decay Function

9. Exponential Decay Function
Year 2004, the population of the Floreana mockingbirds is 137. If
the birds are getting extinct at a rate of 3% per year. How many
of these birds will possibly remain by year 2015?
There would be 114 Floreana
mockingbirds by year 2015.
Formula:
y= a · 𝑏𝑥
, b= 1-r
Solving:
b= 100%-3%= 97%= 0.97
y= 137 · 0.97^6
y= 137 · 0.832972005
=114.117165
=114
Given:
Original number ”a”-
137
Percent decrease- 3%
x- 6 years (from 2004
to 2015)
Looking for:
New number of the
birds by year 2015