Experimental Causal Inference

Experimental
Causal
Inference
Advanced Data Analysis
from an Elementary Point of View

Credits Team
The slides below are derived from the
Chapter 26 of the book “Advanced Data
Analysis from an Elementary Point of
View“ by Cosma Shalizi of the Carnegie
Mellon University, which was created in
order to assist the “Advanced Data
Analysis” course of the CMU.
The example we used is derived from the
notes of Prof. Rosenbaum et al for the
Department of Statistics, of the University
of Pennsylvania
Antigoni-Maria Founta,
UID: 647
Ioannis Athanasiadis,
UID: 607

Overview
➔ CI vs ECI
➔ Why ECI
➔ Example-Driver ECI
➔ Basic Idea
➔ Randomization
◆ Jargon
◆ Causal Identification & Linearity
➔ Open Issues
◆ Randomization Issues
◆ Choice of Levels
◆ Other Issues

CI vs ECI
Causal Inference (CI) is the undertaking of trying to
answer causal questions from empirical data.
Experimental Causal Inference (ECI) is CI that is based on
experiments rather than observations.
“You can only prove causality with statistics.”
F. Mosteller

Why ECI?
Experimental CI is very useful to answer particular questions!
Observations suffer from hidden bias.
Using experiments to prove causality is very powerful,
...but...
Things are much more complicated (need to design the experiments).

Example-driven ECI
● At age 45, Ms. Smith is diagnosed with stage II breast cancer.
● Her oncologist discusses with her two possible treatments: (i) lumpectomy
alone, or (ii) lumpectomy plus irradiation. They decide on (ii).
● Ten years later, Ms. Smith is alive and the tumor has not recurred.
● Her surgeon, Steve, and her radiologist, Rachael debate:
Rachael says: “The irradiation prevented the recurrence – without it, the tumor
would have recurred.”
Steve says: “You can’t know that. It’s a fantasy – you’re making it up. We’ll never
know.”

Basic Idea behind Experimental Design
1. Maximize Useful Variation
2. Eliminate Unhelpful Variation
3. Randomize what we cannot Eliminate

1. Maximize Useful Variation
● If treatments are identified as important regarding causation, then we want to
maximize the possible manipulations in order to spot any interesting behaviour.
● That idea applies even if we want to show that a treatment has no effect.
Basically: we can only learn anything about how Y relates
to X if X varies.

2. Eliminate Unhelpful Variation
A. Precision of Measurement
// Easy to say and often the right thing to do, but typically reaches limits.
B. Homogenization of Units
// Can raise concerns about generalization to a less-homogeneous population.
C. Limiting comparison to similar units
//The principle behind doing a paired t-test rather than an unpaired, and generally of
trying to eliminate the consequences of uncontrolled variation by matching.

3. Randomize what can’t be eliminated
The great trick of Ronald Fisher!*
// Makes the distribution of uncontrolled variables the same across treatments, so they are
statistically homogeneous.
*Author of the book “The arrangement of Field Experiments” (1926), precursor of the “Design
of Experiments” book!

Important: randomly assigned Z!

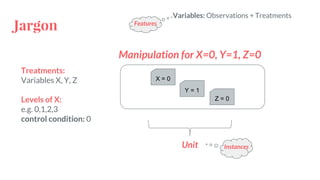
Jargon
Unit
X = 0
Y = 1
Z = 0
Treatments:
Variables X, Y, Z
Levels of X:
e.g. 0,1,2,3
control condition: 0
Manipulation for X=0, Y=1, Z=0
Features
Instances
Variables: Observations + Treatments

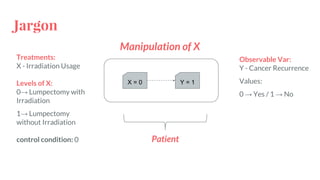
Jargon
Patient
X = 0 Y = 1
Treatments:
X - Irradiation Usage
Levels of X:
0→ Lumpectomy with
Irradiation
1→ Lumpectomy
without Irradiation
control condition: 0
Manipulation of X
Observable Var:
Y - Cancer Recurrence
Values:
0 → Yes / 1 → No

Randomization & Linear Models
In all the below-mentioned cases, linear models (e.g. Linear Regression) can be
sufficient for the estimation of the expected causal effects, either entirely or under
conditions.
● Randomize one treatment
○ Binary Values
Coefficient on X: E[Y|X=1]-E[Y|X=0]
○ Discrete Values
Coefficients on X: E[Y|X=x]-E[Y|X=0] //for all x
● Randomize multiple treatments
E[Y|do(X=x,Z=z)] = μ + fX
(x) + fZ
(z) + fXZ
(x,z) //only if levels of X and Z are discrete

Randomization & Non-Linear Models
● If the levels of the treatments are continuous and have been discretized for the
purpose of the experiment, then linear models are not fitting well.
Why? Because we can’t generalize without concerning the continuous nature of the
treatment!
● It is better to use non-linear models (like a spline or a kernel).
● Important: at least three levels are needed!

Linear vs Non-Linear
In a randomized experiment with
discrete levels of a treatment X, linear
models can be perfectly adequate to
estimate the expected causal effects
for those levels. Instead, when there is a need for
generalization to any values of X we
should use an established regression
model.

Randomization Issues
● Modes of Randomization: Assignment of Treatments
○ IID Assignment: Independent assignment of treatments to each unit
// easy; may lead to lack of balance & issues with constraints
○ Planned Assignment: Assignment according to a fixed schedule applied independently of the
units’ attributes
// complexity; guarantee of balance and constraints
● Perspectives: Units vs Treatments
○ Unit Perspective: fixed units, variate treatments
○ Treatment Perspective: fixed treatment levels, variate unit sampling
// The second is more useful (though harder to understand), because we care about consequences of
treatments, not units!

Choice of Levels
Discretization of continuous values depends on the goal of the experiment.
Goals:
1. Parameter Estimation or Prediction
2. Maximizing Yield
3. Model Discrimination
4. Multiple Goals

Other Issues
● Multiple Manipulated Variables: we want to consider all combinations of all variables.
To achieve that: factorial design!
○ Advantages: can detect all possible interactions
○ Disadvantages: cost!
→ Solution: Partial factorial design!
● Blocking: Divide experimental units into relatively-homogeneous “blocks”.

Other Issues
● “What the experiments died of” aka failures of randomization:
○ Subjectivity of influence (placebo effect, expectations, Hawthorne effect)
○ Threat to generalization to other populations
e.g. experimentation on a school vs generalizing on all schools
○ Non-compliance
○ Non-adequate sample in order to generalize
○ Interference between units

Experimental Causal Inference

More Related Content

What's hot

Viewers also liked

Similar to Experimental Causal Inference

Recently uploaded

Experimental Causal Inference