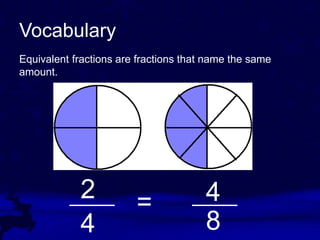
Equivalent fractions are fractions that represent the same amount. To create equivalent fractions, you can multiply or divide the numerator and denominator by the same number. Multiplying makes fractions larger and dividing makes them smaller. Fractions are in simplest form when the numerator and denominator do not share any common factors other than 1. To write a fraction in simplest form, find the greatest common factor of the numerator and denominator and divide both numbers by the greatest common factor.

1. Equivalent Fractions

2. Vocabulary
Equivalent fractions are fractions that name the same
amount.
2
4
= 4
8

3. Creating Equivalent Fractions
•Multiply the numerator and denominator by the same
number.
•Divide the numerator and denominator by the same
number (it has to be a common factor to work with
division)
3
5
We can choose any number to multiply
by. Let’s multiply by 2.
x 2
x 2
=
6
10
So, 3/5 is equivalent to
6/10.

4. If you have larger numbers, you can make equivalent
fractions using division. Divide by a common factor.
28
35
In this example, we can
divide both numbers by 7.
÷ 7
÷ 7
=
4
5
28/35 is equivalent to 4/5.

5. Fractions in Simplest Form
Fractions are in simplest form when the numerator and
denominator do not have any common factors besides 1.
Examples of fractions that are in simplest form:
4
5
2
11
3
8

6. Writing Fractions in Simplest
Form.
• Find the greatest common factor (GCF) of
the numerator and denominator.
• Divide both numbers by the GCF.

7. Example:
20
28
20
1 x 20
2 x 10
4 x 5
28
1 x 28
2 x 14
4 x 7
20: 1, 2, 4, 5, 10, 20
28: 1, 2, 4, 7, 14, 28
Common Factors: 1, 2, 4
GCF: 4
We will divide by 4.
÷ 4
÷ 4
=
5
7
Simplest
Form