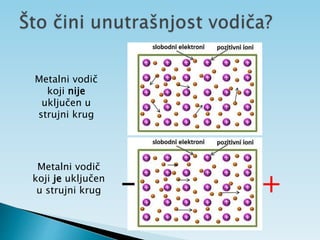
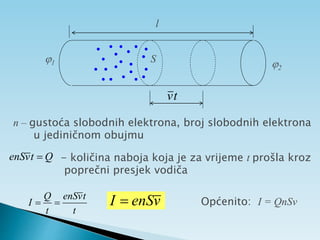
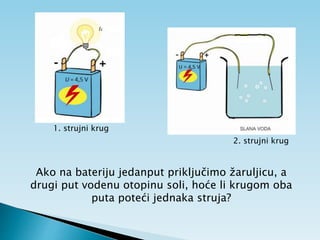
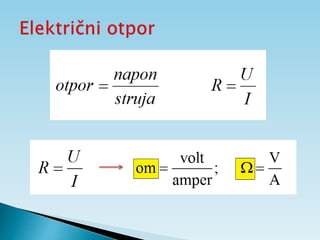
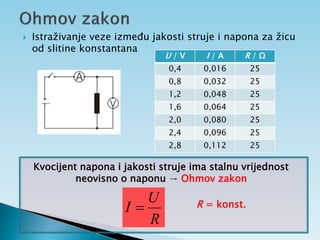
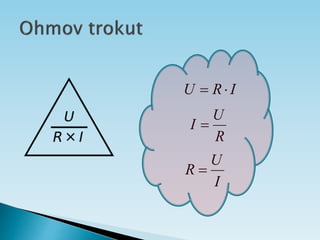
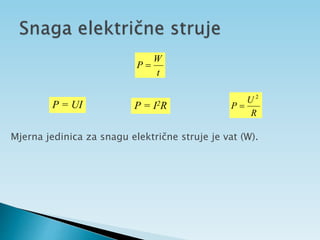
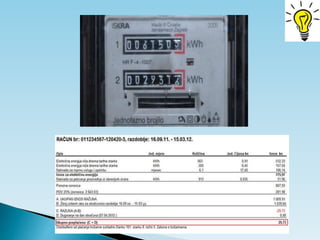
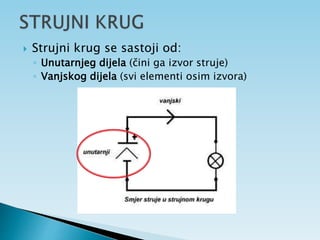
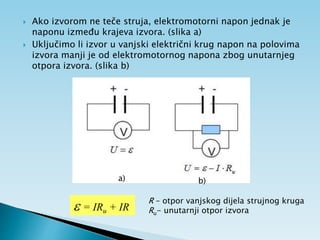
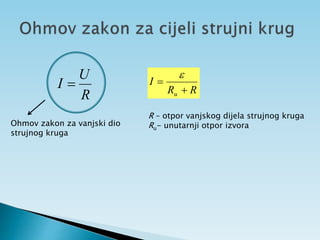
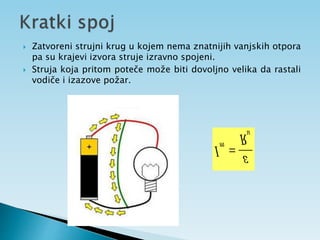
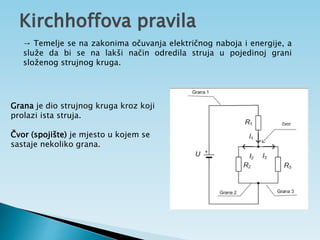
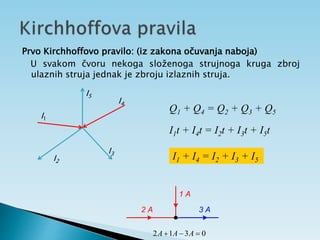
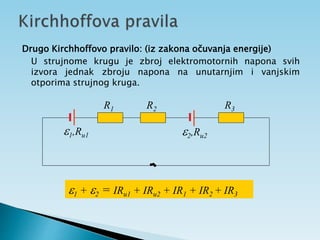
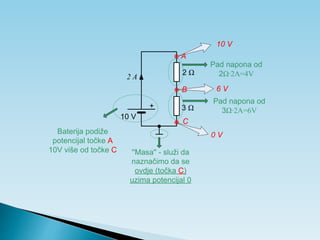
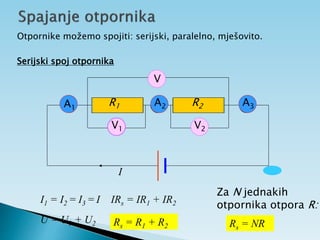
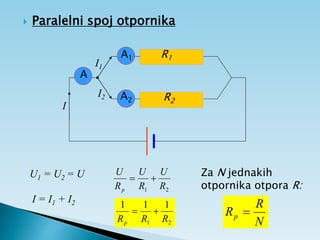
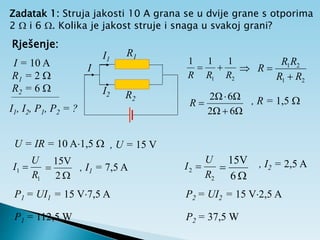
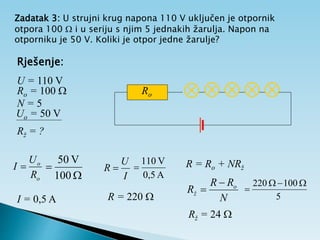
Dokument objašnjava osnovne pojmove vezane uz električnu struju, uključujući usmjereno kretanje elektrona, jakost i gustoću struje te električni otpor. Također sadrži primjere zadataka koji se bave proračunima struje, napona i otpora u različitim električnim krugovima. Uključuje i podatke o energiji i snazi električnih struja te principima mjerenja i analize strujnih krugova.

2. Metalni vodič
koji nije
uključen u
strujni krug
Metalni vodič
koji je uključen
u strujni krug - +

3.  Struju u metalnim vodičima čini usmjereno gibanje
elektrona od negativnog ka pozitivnom polu izvora.
 Struju u tekućinama čine ioni koji se usmjereno gibaju.
 Struju u plinovima čini usmjereno gibanje elektrona i
iona.
 Dogovoreni smjer struje je od pozitivnog ka negativnom
polu izvora, suprotno stvarnome smjeru struje.

4.  Oznaka za jakost električne struje je I
 Jakost električne struje kroz vodič iskazana je
nabojem koji u jednoj sekundi prođe kroz
poprečni presjek vodiča.
 Jedinica jakosti struje je C/s ili amper (A).
 Često se koriste manje jedinice: mikroamper i
miliamper
t
Q
I 
mA
1000
A
1 
μA
000
000
1
A
1 

5.  uređaj za mjerenje jakosti struje
 u strujni krug se uključuje u seriju s trošilom

6.  Oznaka za gustoću struje je J
 Jedinica za gustoću struje je A/m2.
S
I
J 
I – jakost električne struje
S – površina okomita na smjer struje

7. l
1 2
t
v
S
n – gustoća slobodnih elektrona, broj slobodnih elektrona
u jediničnom obujmu
- količina naboja koja je za vrijeme t prošla kroz
poprečni presjek vodiča
t
t
v
enS
t
Q
I 

Q
t
v
enS 
v
enS
I  Općenito: I = QnSv

8.  Zadatak 1: Koliko elektrona svake sekunde prođe
presjekom vodiča kada njime teče struja jakosti 1
A?
 Zadatak 2: Struja jakosti 2 A teče žicom tijekom
vremena od 2 min. Koliki ukupni električni naboj i
koliko elektrona prođe kroz žicu tijekom toga
vremena?
 Zadatak 3: Srebrnim vodičem površine presjeka 2,5
mm2 teče stalna struja jakosti 5 A. Izračunajmo:
a)broj elektrona koji svake sekunde prođe površinom
presjeka vodiča
b) srednju brzinu usmjerenog gibanja slobodnih elektrona
ako je njihova gustoća u srebru 5,8·1028 m-3.

9. S = 2,5 mm2
I = 5 A
a) N = ?
N = 3,125·1019
b) ?

v
v
enS
I 
enS
I
v 
2
6
3
-
28
19
m
10
5
,
2
m
10
5,8
C
10
6
,
1
A
5








v
-1
4
s
m
10
2 


v
n = 5,8·1028 m-3
= 2,5·10-6 m2
t
Q
I 
t
Ne

e
It
N 

C
10
1,6
s
1
A
5
19
-



N

10. 1. strujni krug
2. strujni krug
Ako na bateriju jedanput priključimo žaruljicu, a
drugi put vodenu otopinu soli, hoće li krugom oba
puta poteći jednaka struja?

13.  Električni otpor vodiča ovisi o:
◦ vrsti materijala (otpornost )
◦ duljini vodiča
◦ površini presjeka vodiča S
S
l
R 

ZAKON ELEKTRIČNOG OTPORA

l
Električni otpor ovisi o vrsti
tvari, proporcionalan je
duljini vodiča, a obrnuto je
proporcionalan površini
presjeka vodiča.

14.  Zadatak 1: Koliki je otpor bakrene žice duljine 1 km i
promjera 2 mm?
 Zadatak 2: Mjedena žica poprečnog presjeka 0,5 mm2 i
duljine 50 m priključena je na napon 8 V. Kolika je
jakost struje kroz žicu?
 Zadatak 3: Srebrna žica duga je 0,5 m, ima površinu
presjeka 0,8 mm2 i spojena je na bateriju napona 6 V.
Kolika struja teče žicom? (ρ = 1,6·10-8 Ωm)

15.  Istraživanje veze između jakosti struje i napona za žicu
od slitine konstantana
Kvocijent napona i jakosti struje ima stalnu vrijednost
neovisno o naponu → Ohmov zakon
R
U
I  R = konst.
U / V I / A R / Ω
0,4 0,016 25
0,8 0,032 25
1,2 0,048 25
1,6 0,064 25
2,0 0,080 25
2,4 0,096 25
2,8 0,112 25

16. R
U
I 
I
R
U 

I
U
R 

17.  Grafički prikaz
ovisnosti jakosti
struje o naponu
nazivamo U, I –
karakteristika
vodiča.
 Ako je R = konst.
Tada je U,I-
karakteristika
pravac koji prolazi
ishodištem
koordinatnog
sustava. (slika 1)
Slika 1

18.  Omski vodiči – vodiči za koje vrijedi Ohmov zakon,
odnosno vrijednost otpora ne ovisi o naponu (npr.
metali)
 Neomski vodiči – vodiči za koje ne vrijedi Ohmov zakon,
vrijednost otpora se mijenja ovisno o naponu (npr.
poluvodička dioda)

19.  Zadatak 1: Možemo li voltmetrom koji ima mjernu
ljestvicu do 20 V izmjeriti napon na krajevima otpornika
4,2 Ω kad njime teče struja jakosti 5,3 A?
 Zadatak 2: Struja jakosti 100 mA i veće izaziva stezanje
srčanog mišića, što može biti smrtonosno. Je li čovjekov
život u opasnosti kada mu se tijelo nađe pod naponom
220 V ako je otpor tijela 1000 Ω?
 Zadatak 3: Kroz žarulju spojenu na napon 4,5 V teče
struja 0,05 A. Izračunajmo:
a) koliki je otpor žarulje
b) kolika bi struja tekla kroz žarulju ako je spojimo na
napon 1,5 V?

20. Rad što ga izvor napona mora obaviti da bi potekla struja I
kroz trošilo otpora R u vremenu t jednak je:
W = UQ = UIt W = UIt = IRIt W = I2Rt Rt
R
U
2
2
 t
R
U
W
2

Električna energija – električna potencijalna energija +
kinetička energija slobodnih elektrona.
Mjerna jedinica za rad električne struje i električnu energiju
je džul (J). Često se koristi i kilovatsat (kWh).
1 kWh = 3,6 · 106 J

21. t
W
P 
R
U
P
2

P = UI P = I2R
Mjerna jedinica za snagu električne struje je vat (W).

22.  Električna energija se ne troši, nego samo pretvara u
drugi oblik energije (toplinsku, mehaničku, svjetlosnu...)
 Električno brojilo mjeri pretvorenu električnu energiju u
kilovatsatima.

24. Zadatak 1:Grijalo priključeno na napon 220 V ima
snagu 800 W.
a) Koliki je otpor grijala?
b) Kolika je jakost struje kroz grijalo?
Rješenje:
U = 220 V
P = 800 V
a) R = ?
2
R
U
P 
P
U
R
2


800W
V)
220
( 2
 R = 60,5 
b) I = ? P = UI
U
P
I 
V
220
W
800
 I = 3,64 A


25. Zadatak 2: Struja jakosti 10 A prolazi bakrenom žicom duljine
1 m i površine presjeka 0,1mm2. Koliko se topline oslobodi u
žici svake sekunde? Električna otpornost bakra je
0,017210-6  m.
Rješenje:
I = 10 A
l = 1 m
S = 0,1 mm2 = 0,110-6 m2
t = 1 s
Q = ?
Q = W= I2Rt
S
l
R 

t
S
l
I
Q 
2
 s
1
m
10
0,1
m
1
m
10
0172
,
0
)
A
10
( 6
-
6
2






 
Q = 17,2 J
 = 0,017210-6  m

26. Zadatak 3: Zaboravili ste isključiti žarulju snage 100 W pa je ona
svijetlila 24 sata. Koliko ćete platiti električnu energiju pretvorenu
u žarulji ako 1 kWh električne energije stoji 0,90 kuna?
Zadatak 4: Električnim glačalom otpora 20 Ω prolazi struja jakosti
5 A. Kolika će se toplina prenijeti na glačalo tijekom 30 sekundi?
Zadatak 5: Koliku električnu snagu troši električna žarulja s
otporom R = 240 Ω, kada njome teče struja jakosti I =0,5A?7
Zadatak 6: Za 1 sat 1500 C naboja prođe presjekom vodiča otpora
20 Ω. Koliki je napon na krajevima vodiča?
Zadatak 7: Žaruljom otpora R, priključenom na bateriju napona 12
V, zanemarivog unutarnjeg otpora, teče struja 0,6 μA. Izračunajte:
a) Otpor žarulje
b) Snagu žarulje
c) Energiju koju elektroni predaju žarulji svake sekunde
Rješenja: 2,16 kn, 15000 J, 60 W, 8,4 V, 2·107 Ω, 7,2 ·10-6 W, 7,2
·10-6 J

27.  Strujni krug se sastoji od:
◦ Unutarnjeg dijela (čini ga izvor struje)
◦ Vanjskog dijela (svi elementi osim izvora)

28.  Električni izvor
◦ bilo koji sustav koji stvara elektromotorni napon
◦ uređaji u kojima se neki od oblika energije (mehanička,
svjetlosna, kemijska...) pretvara u električnu energiju.

29.  Električni izvor
◦ Ima dva pola (plus i minus) različitih potencijala → stvara se
napon, izvor održava razliku potencijala,
razdvajanje raznovrsnih naboja
◦ Izvori istosmjerne (baterije, akumulator) i
izmjenične (generatori u elektranama) struje.
 Elektromotorni napon ℇ (elektromotorna sila)
◦ Unutarnji napon električnog izvora
◦ Rad koji neelektrična sila vrši nad jediničnim nabojem pri
premještanju naboja.
Q
Wne



30.  Ako izvorom ne teče struja, elektromotorni napon jednak je
naponu između krajeva izvora. (slika a)
 Uključimo li izvor u vanjski električni krug napon na polovima
izvora manji je od elektromotornog napona zbog unutarnjeg
otpora izvora. (slika b)
 = IRu + IR
R – otpor vanjskog dijela strujnog kruga
Ru- unutarnji otpor izvora
a) b)

31. R
R
I
u 


R
U
I 
R – otpor vanjskog dijela strujnog kruga
Ru- unutarnji otpor izvora
Ohmov zakon za vanjski dio
strujnog kruga

32.  Zatvoreni strujni krug u kojem nema znatnijih vanjskih otpora
pa su krajevi izvora struje izravno spojeni.
 Struja koja pritom poteče može biti dovoljno velika da rastali
vodiče i izazove požar.
u
m
R
I



33.  Zadatak 1: Elektromotorni napon izvora iznosi 12 V, a
struja kratkog spoja 6 A. Izračunajte:
a) unutarnji otpor izvora
b) jakost struje kada je u njemu vanjski otpor 10 Ω
Rješenje: a) Ru = 2Ω b) I = 1A

34. Zadatak 2: Otpornik od 12  spojimo na izvor
elektromotornog napona 6,3 V i unutarnjeg otpora 0,6 .
Izračunajte:
a) napon na otporniku
b) snagu na otporniku
Rješenje:
R = 12 
 = 6,3 V
Ru = 0,6 
U, P = ?
R
R
I
u 


V
12
6
,
0
V
3
,
6


 = 0,5 A
U = IR = 0,5 A12  , U = 6 V P = UI = 6 V0,5 A
P = 3 W

35. Zadatak 3: Graf na slici prikazuje međusobnu ovisnost jakosti
struje i napona na vanjskom dijelu strujnog kruga. Odredite:
a) elektromotorni napon
b) jakost struje u kratkom spoju
c) unutarnji otpor izvora.
Rješenje:
I /A
U/ V
2
4
6
4 8 12
 = 4,5 V
Im = 9 A u
m
R
I


m
u
I
R



A
9
V
5
,
4
 , Ru = 0,5 

36. Zadatak 4: Nekim krugom u kratkom spoju teče struja 100 A,
a kada je u krugu otpornik otpora 14  jakost je struje 10 A.
Koliki su unutarnji otpor i elektromotorni napon izvora?
Rješenje:
Im = 100 A
R = 14 
I = 10 A
Ru , = ?
u
m
R
I

   = ImRu
 = IRu + IR
ImRu = IRu + IR
I
I
IR
R
m
u


10A
-
100A
14
A
10 


Ru = 1,56 
 = 100 A1,56 
 = 156 V

37. Zadatak 5: Pri naponu na vanjskom dijelu strujnog kruga
1,45 V krugom teče struja jakosti 0,2 A, a pri naponu 1,25 V
jakost struje je 0,6 A. Izračunajte unutarnji otpor i
elektromotorni napon izvora.
Rješenje:
U1 = 1,45 V
I1 = 0,2 A
U2 = 1,25 V
I2 = 0,6 A
Ru , = ?
 = IRu + IR IR = U
 = IRu + U
 = I1Ru + U1 ,  = I2Ru + U2
I1Ru + U1 = I2Ru + U2
I1Ru – I2Ru = U2 – U1
2
1
1
2
I
I
U
U
Ru



A
0,6
-
A
2
,
0
V
1,45
-
V
25
,
1
 Ru = 0,5 
 = 0,2 A0,5  + 1,45 V  = 1,55 V

38. Kirchhoffova pravila
Grana je dio strujnog kruga kroz koji
prolazi ista struja.
Čvor (spojište) je mjesto u kojem se
sastaje nekoliko grana.
→ Temelje se na zakonima očuvanja električnog naboja i energije, a
služe da bi se na lakši način odredila struja u pojedinoj grani
složenog strujnog kruga.

39. Prvo Kirchhoffovo pravilo: (iz zakona očuvanja naboja)
U svakom čvoru nekoga složenoga strujnoga kruga zbroj
ulaznih struja jednak je zbroju izlaznih struja.
Q1 + Q4 = Q2 + Q3 + Q5
I1t + I4t = I2t + I3t + I5t
I1 + I4 = I2 + I3 + I5
I1
I5
I2
I3
I4
2 A
1 A
3 A
2 1 3 0
A A A

 

40. Drugo Kirchhoffovo pravilo: (iz zakona očuvanja energije)
U strujnome krugu je zbroj elektromotornih napona svih
izvora jednak zbroju napona na unutarnjim i vanjskim
otporima strujnog kruga.
1,Ru1 2,Ru2
R1 R2 R3
1 + 2 = IRu1 + IRu2 + IR1 + IR2 + IR3

41. 10 V
3 Ω
2 Ω
+
2 A
''Masa'' - služi da
naznačimo da se
ovdje (točka C)
uzima potencijal 0
A
B
C
10 V
0 V
6 V
Baterija podiže
potencijal točke A
10V više od točke C
Pad napona od
2Ω∙2A=4V
Pad napona od
3Ω∙2A=6V

42. Otpornike možemo spojiti: serijski, paralelno, mješovito.
Serijski spoj otpornika
U = U1 + U2
I1 = I2 = I3 = I
I
IRs = IR1 + IR2
Rs = R1 + R2 Rs = NR
Za N jednakih
otpornika otpora R:
R1 R2
V
V1 V2
A1
A3
A2

43.  Paralelni spoj otpornika
R1
R2
U1 = U2 = U
I = I1 + I2
2
1 R
U
R
U
R
U
p


2
1
1
1
1
R
R
Rp


Za N jednakih
otpornika otpora R:
N
R
Rp 
I
I2
I1
A2
A
A1

44. Zadatak 1: Struja jakosti 10 A grana se u dvije grane s otporima
2  i 6 . Kolika je jakost struje i snaga u svakoj grani?
Rješenje:
I = 10 A
R1 = 2 
R2 = 6 
I1, I2, P1, P2 = ?
I
I1
I2
R1
R2
1
1
1
2
1 R
R
R


2
1
2
1
R
R
R
R
R



, R = 1,5 
U = IR = 10 A1,5  , U = 15 V
1
1
R
U
I 


2
V
15
, I1 = 7,5 A
P1 = UI1 = 15 V7,5 A
, I2 = 2,5 A
6Ω
2Ω
6Ω
2Ω



R
P1 = 112,5 W
2
2
R
U
I 


6
V
15
P2 = UI2 = 15 V2,5 A
P2 = 37,5 W

45. Zadatak 2: Tri su otpornika spojena u strujni krug prema shemi na
slici. Izračunajte: a) ukupni otpor b) jakost struje kroz svaki od
otpornika c) napon na svakom od otpornika
Unutarnji otpor izvora zanemarite.
Rješenje:
U = 24 V
R1 = 50 
R2 = 100 
R3 = 200 







200
100
200
100
R23 =
3
2
3
2
R
R
R
R

R23 = 66,7 
R = R1 + R23 = 50  + 66,7 
R = 116,7 
24 V
50 
100 
200 
I1 I2
I3
R
U
I 
1


116,7
V
24
I1 = 0,206 A
U 23 = I1R23 = 0,206 A66,7 
U 23 = 13,7 V
U1 = I1R1 = 0,206 A50 
U1 = 10,3 
2
23
2
R
U
I 


100
V
7
,
13
, I2 = 0,137 A
3
23
3
R
U
I 


200
V
7
,
13 , I3 = 0,069 A

46. Zadatak 3: U strujni krug napona 110 V uključen je otpornik
otpora 100  i u seriju s njim 5 jednakih žarulja. Napon na
otporniku je 50 V. Koliki je otpor jedne žarulje?
Rješenje:
U = 110 V
Ro = 100 
N = 5
Uo = 50 V
Rž = ?
    
Ro
o
o
R
U
I 


100
V
50
I = 0,5 A
I
U
R 
A
0,5
V
10
1

R = 220 
R = Ro + NRž
N
R
R
R o
ž


5
100
20
2 



Rž = 24 

47.  Galvanometar – uređaj koji služi za mjerenje električnih
veličina: jakosti struje, napona i električnog otpora.
Prolaskom struje kroz galvanometar njegova se kazaljka
zakreće.
 Ovisno o tome kako je uključen u strujni krug galvanometar
može biti: ampermetar, voltmetar i ommetar.

48.  Ampermetar – galvanometar koji služi za mjerenje jakosti
struje.
 Električni otpor ampermetra treba biti vrlo malen kako se
njegovim uključivanjem u strujni krug jakost struje u krugu
ne bi znatno smanjila.
 Ampermetar se u strujni krug uključuje serijski.

49.  Voltmetar– galvanometar koji služi za mjerenje napona na
krajevima otpornika.
 Električni otpor voltmetra treba biti velik kako bi njegov
utjecaj na ukupni otpor i jakost struje u krugu bio što manji.
 Voltmetar se u strujni krug uključuje paralelno na trošilo.