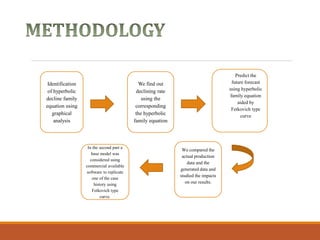
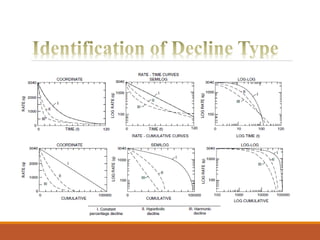
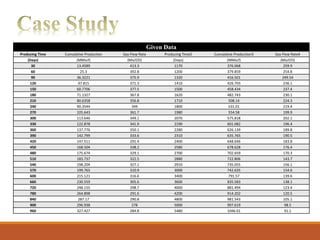
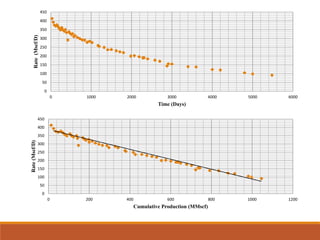
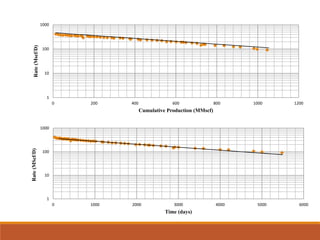
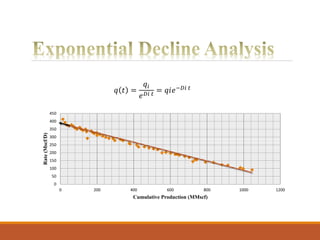
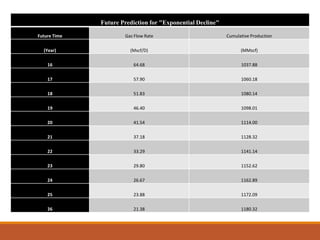
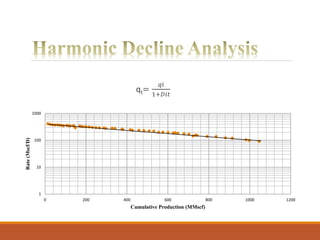
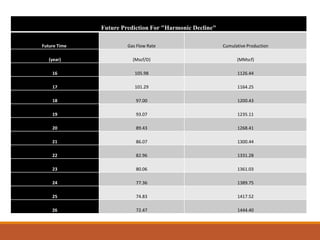
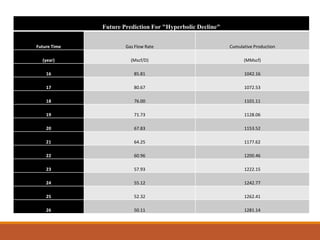
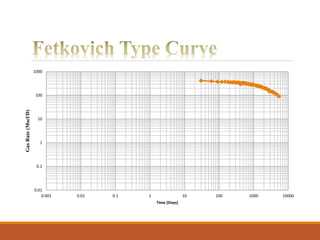
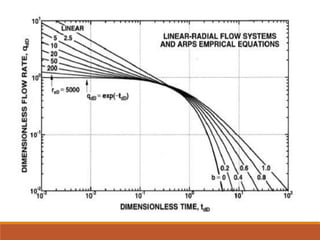
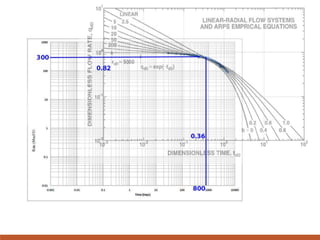
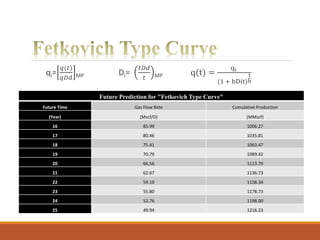
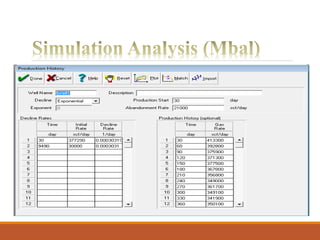
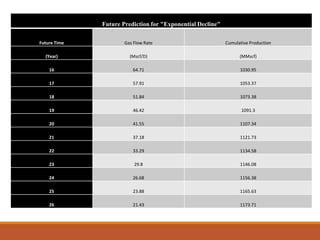
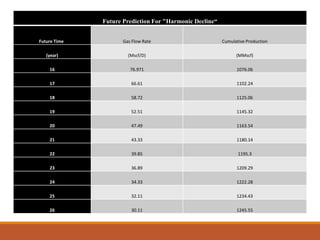
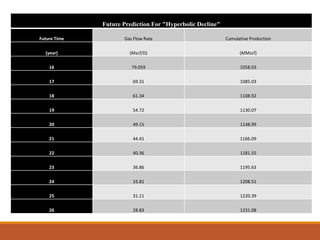
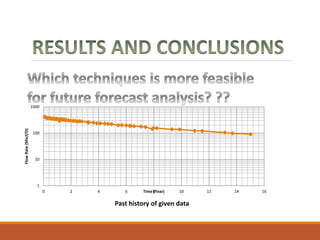
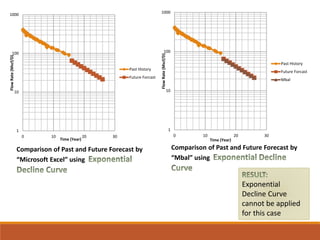
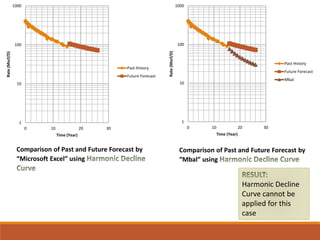
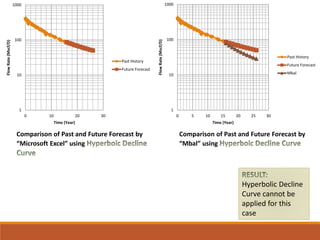
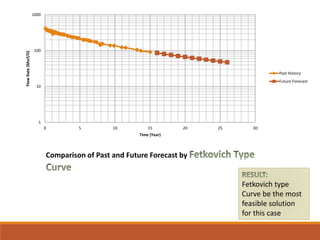
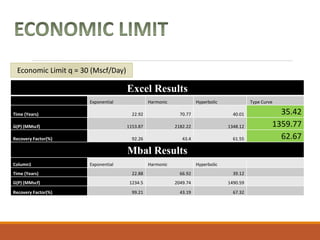
The document discusses decline curve analysis (DCA) for estimating reserves in conventional and unconventional reservoirs. It proposes using a Fetkovich type curve method in Microsoft Excel and comparing results to commercial software. The key steps are identifying the hyperbolic decline curve from production data, forecasting future production using the curve equation, and comparing actual vs predicted production to evaluate accuracy. DCA provides more accurate reserve estimates than other methods using less data as it accounts for production trends over time.

5. •Importance
•Unconventional reservoirs
•Arps Vs. Fetkovich type
•Requires less data and give better estimates

6. “Overview of proposed method to calculate reserves
for conventional reservoirs and interpretation of case
study using Microsoft Excel and MBAL”

7. Identification
of hyperbolic
decline family
equation using
graphical
analysis
Predict the
future forecast
using hyperbolic
family equation
aided by
Fetkovich type
curve
We compared the
actual production
data and the
generated data and
studied the impacts
on our results.
We find out
declining rate
using the
corresponding
the hyperbolic
family equation
In the second part a
base model was
considered using
commercial available
software to replicate
one of the case
history using
Fetkovich type
curve.

8. •Effective future forecast
•Overview of composite profile decline curve
analysis
•Comparative Analysis between MICROSOFT
EXCEL & MBAL

9. •Economic time limit computation more precisely
•More precise forecast analysis
•Effective computation of recoverable reserves

10. Introduction to DCA

11. Classical curve fit of historical production data
•Exponential Decline
•Harmonic Decline
•Hyperbolic Decline
Type-curve matching technique
•Fetkovich Type Curve
•Carter Type Curve

12. Arps’ Equation
q(t) =
qi
(1 + bDit)
1
b
Where,
b = Decline exponent t = Time, days
qi = Initial rate, Mscf/day Di = Initial decline rate, day-1

14. Decline curves characterized by 3 factors:
Initial Production Rate
Curvature of decline
Rate of decline
Ikuko Analysis
Production must Have been stable
Stable reservoir conditions
DCA is used in evaluation of new investment

15. •Stable production
•Stable reservoir conditions
•Boundary dominant conditions

16. Theoretical plots of solutions.
 Uses log-log graph.
Find the flow characteristics of individual well.

17. • Fetkovich Type Curve
•Carter Type Curve

18. Based on analytical solutions
Can be used for analyzing hydraulically fractured wells
Include both flow regimes.

19. Plot q(t) & Gp (t) vs time on log-log paper
Match the production data to the best fitting type curve
Record the values of corresponding parameters.

21. ASSUUMPTIONS:
•Constant BHP
•Permeability and skin
•Boundary Conditions
•Volumetric Reservoir

22. •Fetkovich (1980)
•Holditch (2006)
•Holditch and Madani (2010)
•Naik (2013)

23. Given Data
Producing Time Cumulative Production Gas Flow Rate Producing Time2 Cumulative Production3 Gas Flow Rate4
(Days) (MMscf) (Mscf/D) (Days) (MMscf) (Mscf/D)
30 13.4589 413.3 1170 376.068 259.9
60 25.3 392.8 1200 379.859 254.8
90 36.3221 375.9 1320 416.501 249.54
120 47.815 371.3 1410 426.793 236.1
150 60.7706 377.5 1500 458.434 237.4
180 71.1327 367.8 1620 482.743 230.1
210 80.6358 356.8 1710 508.14 224.3
240 90.3544 349 1800 531.01 219.4
270 105.643 361.7 1980 554.58 199.9
300 113.646 349.1 2070 575.818 202.1
330 122.878 341.9 2190 601.082 196.4
360 137.776 350.1 2280 626.139 189.8
390 142.799 333.6 2310 635.765 190.5
420 147.511 291.4 2400 648.646 183.8
450 168.504 338.2 2580 678.628 176.4
480 175.674 329.1 2700 702.659 170.3
510 183.737 322.5 2880 722.806 143.7
540 198.204 327.1 2910 735.055 156.1
570 199.765 310.9 3000 742.635 154.6
600 215.121 316.6 3400 791.57 139.6
660 230.559 305.6 3600 835.583 138.1
720 248.155 298.7 4000 881.494 123.4
780 264.898 291.6 4200 914.202 120.5
840 287.17 290.8 4800 981.543 105.1
900 296.938 278 5000 997.619 98.5
960 327.427 284.8 5480 1046.01 91.1

24. 0
50
100
150
200
250
300
350
400
450
0 1000 2000 3000 4000 5000 6000
Rate(Mscf/D)
Time (Days)
0
50
100
150
200
250
300
350
400
450
0 200 400 600 800 1000 1200
Rate(Mscf/D)
Cumulative Production (MMscf)

25. 1
10
100
1000
0 200 400 600 800 1000 1200
Rate(Mscf/D)
Cumulative Production (MMscf)
1
10
100
1000
0 1000 2000 3000 4000 5000 6000
Rate(MScf/D)
Time (days)

26. 0
50
100
150
200
250
300
350
400
450
0 200 400 600 800 1000 1200
Rate(Mscf/D)
Cumulative Production (MMscf)
𝑞 𝑡 =
𝑞𝑖
𝑒 𝐷𝑖 𝑡
= 𝑞𝑖𝑒−𝐷𝑖 𝑡

27. Future Prediction for "Exponential Decline"
Future Time Gas Flow Rate Cumulative Production
(Year) (Mscf/D) (MMscf)
16 64.68 1037.88
17 57.90 1060.18
18 51.83 1080.14
19 46.40 1098.01
20 41.54 1114.00
21 37.18 1128.32
22 33.29 1141.14
23 29.80 1152.62
24 26.67 1162.89
25 23.88 1172.09
26 21.38 1180.32

28. qt=
𝑞i
1+𝐷𝑖𝑡
1
10
100
1000
0 200 400 600 800 1000 1200
Rate(Mscf/D)
Cumulative Production (MMscf)

29. Future Prediction For "Harmonic Decline"
Future Time Gas Flow Rate Cumulative Production
(year) (Mscf/D) (MMscf)
16 105.98 1126.44
17 101.29 1164.25
18 97.00 1200.43
19 93.07 1235.11
20 89.43 1268.41
21 86.07 1300.44
22 82.96 1331.28
23 80.06 1361.03
24 77.36 1389.75
25 74.83 1417.52
26 72.47 1444.40

30. qt =
𝑞𝑖
(1+𝐷𝑖𝑏𝑡)1/𝑏
Iteration Technique

31. Future Prediction For "Hyperbolic Decline"
Future Time Gas Flow Rate Cumulative Production
(year) (Mscf/D) (MMscf)
16 85.81 1042.16
17 80.67 1072.53
18 76.00 1101.11
19 71.73 1128.06
20 67.83 1153.52
21 64.25 1177.62
22 60.96 1200.46
23 57.93 1222.15
24 55.12 1242.77
25 52.32 1262.41
26 50.11 1281.14

32. 0.01
0.1
1
10
100
1000
0.001 0.01 0.1 1 10 100 1000 10000
GasRate(Mscf/D)
Time (Days)

35. qi=
𝑞(𝑡)
𝑞𝐷𝑑 MP Di=
𝑡𝐷𝑑
𝑡 MP q(t) =
qi
(1 + bDit)
1
b
Future Prediction for "Fetkovich Type Curve"
Future Time Gas Flow Rate Cumulative Production
(Year) (Mscf/D) (MMscf)
16 85.99 1006.27
17 80.46 1035.81
18 75.41 1063.47
19 70.79 1089.42
20 66.56 1113.79
21 62.67 1136.73
22 59.10 1158.34
23 55.80 1178.73
24 52.76 1198.00
25 49.94 1216.23

37. Future Prediction for "Exponential Decline"
Future Time Gas Flow Rate Cumulative Production
(Year) (Mscf/D) (MMscf)
16 64.71 1030.95
17 57.91 1053.37
18 51.84 1073.38
19 46.42 1091.3
20 41.55 1107.34
21 37.18 1121.73
22 33.29 1134.58
23 29.8 1146.08
24 26.68 1156.38
25 23.88 1165.63
26 21.43 1173.71

38. Future Prediction For "Harmonic Decline“
Future Time Gas Flow Rate Cumulative Production
(year) (Mscf/D) (MMscf)
16 76.971 1076.06
17 66.61 1102.24
18 58.72 1125.06
19 52.51 1145.32
20 47.49 1163.54
21 43.33 1180.14
22 39.85 1195.3
23 36.89 1209.29
24 34.33 1222.28
25 32.11 1234.43
26 30.11 1245.55

39. Future Prediction For "Hyperbolic Decline"
Future Time Gas Flow Rate Cumulative Production
(year) (Mscf/D) (MMscf)
16 79.059 1058.03
17 69.31 1085.03
18 61.34 1108.92
19 54.72 1130.07
20 49.15 1148.99
21 44.41 1166.09
22 40.36 1181.55
23 36.86 1195.63
24 33.81 1208.51
25 31.11 1220.39
26 28.83 1231.08

40. 1
10
100
1000
0 2 4 6 8 10 12 14 16
FlowRate(Mscf/D)
Time (Year)
Past history of given data

41. 1
10
100
1000
0 10 20 30
FlowRate(Mscf/D)
Time (Year)
Past History
Future Forcast
1
10
100
1000
0 10 20 30
FlowRate(Mscf/D)
Time (Year)
Past History
Future Forcast
Mbal
Comparison of Past and Future Forecast by
“Microsoft Excel” using
Comparison of Past and Future Forecast by
“Mbal” using
Exponential
Decline Curve
cannot be applied
for this case

42. 1
10
100
1000
0 10 20 30
Rate(Mscf/D)
Time (Year)
Past History
Future Forecast
1
10
100
1000
0 10 20 30
Rate(Mscf/D)
Time (Year)
Past History
Future Forecast
Mbal
Comparison of Past and Future Forecast by
“Microsoft Excel” using
Comparison of Past and Future Forecast by
“Mbal” using
Harmonic Decline
Curve cannot be
applied for this
case

43. 1
10
100
1000
0 10 20 30
FlowRate(Mscf/D)
Time (Year)
Past History
Future Forecast
1
10
100
1000
0 5 10 15 20 25 30
FlowRate(Mscf/D)
Time (Year)
Past History
Future Forecast
Mbal
Comparison of Past and Future Forecast by
“Microsoft Excel” using
Hyperbolic Decline
Curve cannot be
applied for this
case
Comparison of Past and Future Forecast by
“Mbal” using

44. 1
10
100
1000
0 5 10 15 20 25 30
FlowRate(Mscf/D)
Time (Year)
Past History
Future Forecast
Comparison of Past and Future Forecast by
Fetkovich type
Curve be the most
feasible solution
for this case

45. Excel Results
Exponential Harmonic Hyperbolic Type Curve
Time (Years) 22.92 70.77 40.01 35.42
G(P) (MMscf) 1153.87 2182.22 1348.12 1359.77
Recovery Factor(%) 92.26 43.4 61.55 62.67
Mbal Results
Column1 Exponential Harmonic Hyperbolic
Time (Years) 22.88 66.92 39.12
G(P) (MMscf) 1234.5 2049.74 1490.59
Recovery Factor(%) 99.21 43.19 67.32
Economic Limit q = 30 (Mscf/Day)

46. •DCA can be applied on any type of reservoir whether it is gas reservoir or oil reservoir
with equal accuracy & whether it is conventional one or unconventional and we just
need past production history.
•While applying DCA for unconventional reserves just keep in mind the very low
permeability factor because our reservoir should be in the pseudo steady state.
•DCA can be used to estimate ultimate gas recovery, remaining productive life of the
field at some abandonment pressure, drainage radius and pore volume, skin &
permeability of the reservoir.

47. •DCA is much more accurate and requires less data as compared to the
MBE technique and volumetric technique, since it predicts future
forecast using past production history and it accommodates the time
factor as well, i.e. how much time this reservoir will take to recover this
amount of reserves and in petroleum sector “time is money”.

48. •DCA can be applied only if the past production trends follows one of the “Hyperbolic
family of equations i.e. exponential, hyperbolic or harmonic trends”, if it is not
happening, we cannot estimate reserves in an effective way.
•DCA can only give precise future estimates if production controlling factors will
continue in the future following the past trends & production mechanism will remains
same e.g. if we install artificial lift system on a reservoir after DCA estimation, in that
case DCA results becomes erroneous.

49. •Utilize all available techniques:
Utilizes curve matching technique as well other than hyperbolic equations for
high effective results.
•Comparison between the data base and software base:
Use of data base and compares their results with commercial available
software to estimates better reserves.
•Utilize modern techniques for unconventional reservoirs:
Use of modern techniques like “Exponental+Hyperbolic decline” & “Power
exponential decline” for unconventional reservoirs etc.

50. https://www.onepetro.org/download/conference-paper/IPTC-18188-
MS?id=conference-paper%2FIPTC-18188-MS
https://www.onepetro.org/search?q=iptc-14801-
ms&peer_reviewed=&published_between=&from_year=&to_year=&rows=10
https://www.onepetro.org/download/conference-paper/SPE-170945-
MS?id=conference-paper%2FSPE-170945-MS
Reservoir Engineering Handbook by Tarek Ahmed (Fourth Edition)
John Lee and Robert A. Wattenbarger. Copyright 1996. Gas Reservoir
Engineering. Society of Petroleum Engineers Inc
E.I. Shirman. Universal Approach to Decline Curve Analysis. Louisiana State
University.
J.J Arps. 1994. Decline Curve Analysis. A.I.M.E

51. QESTIONS ARE
WELCOME…