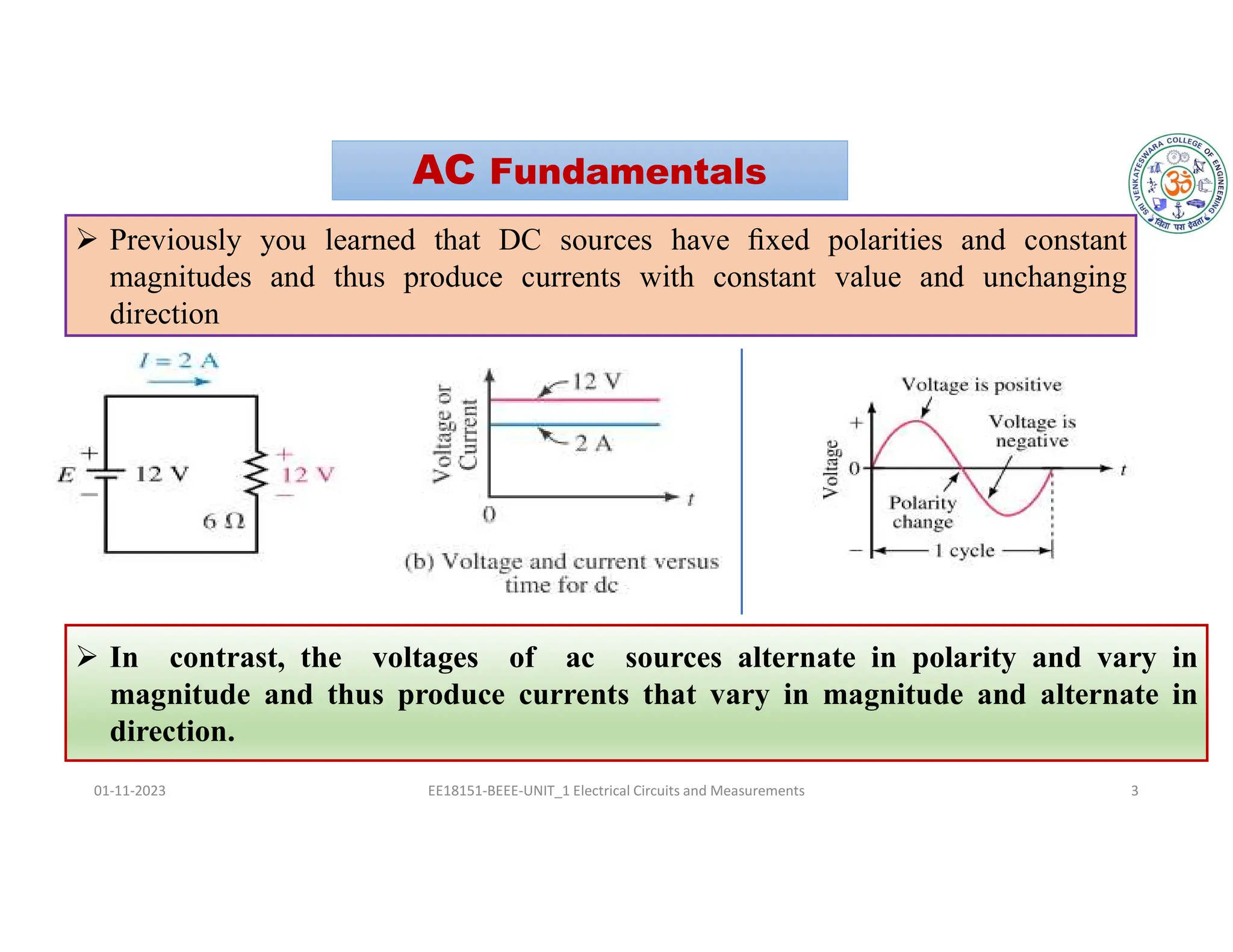
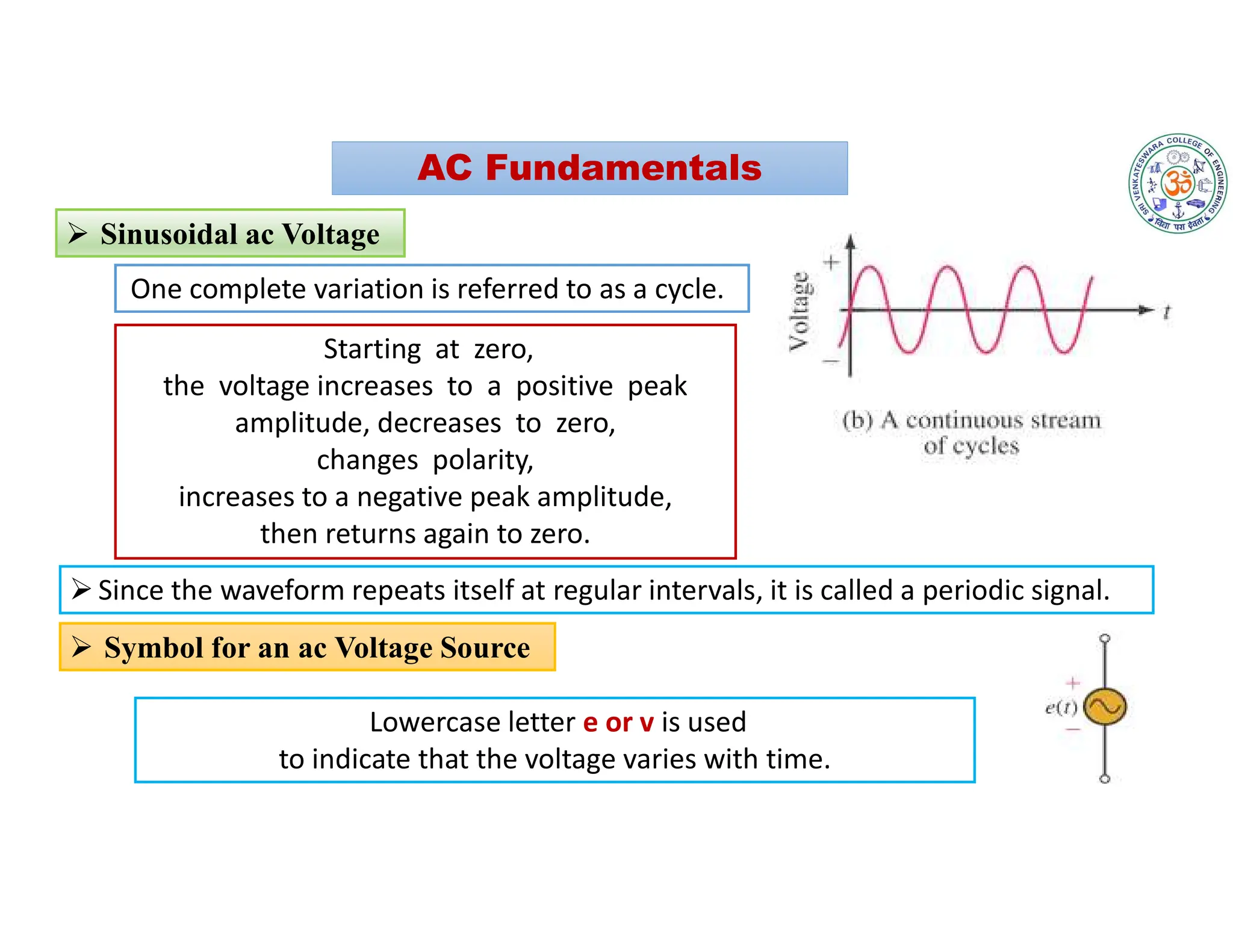
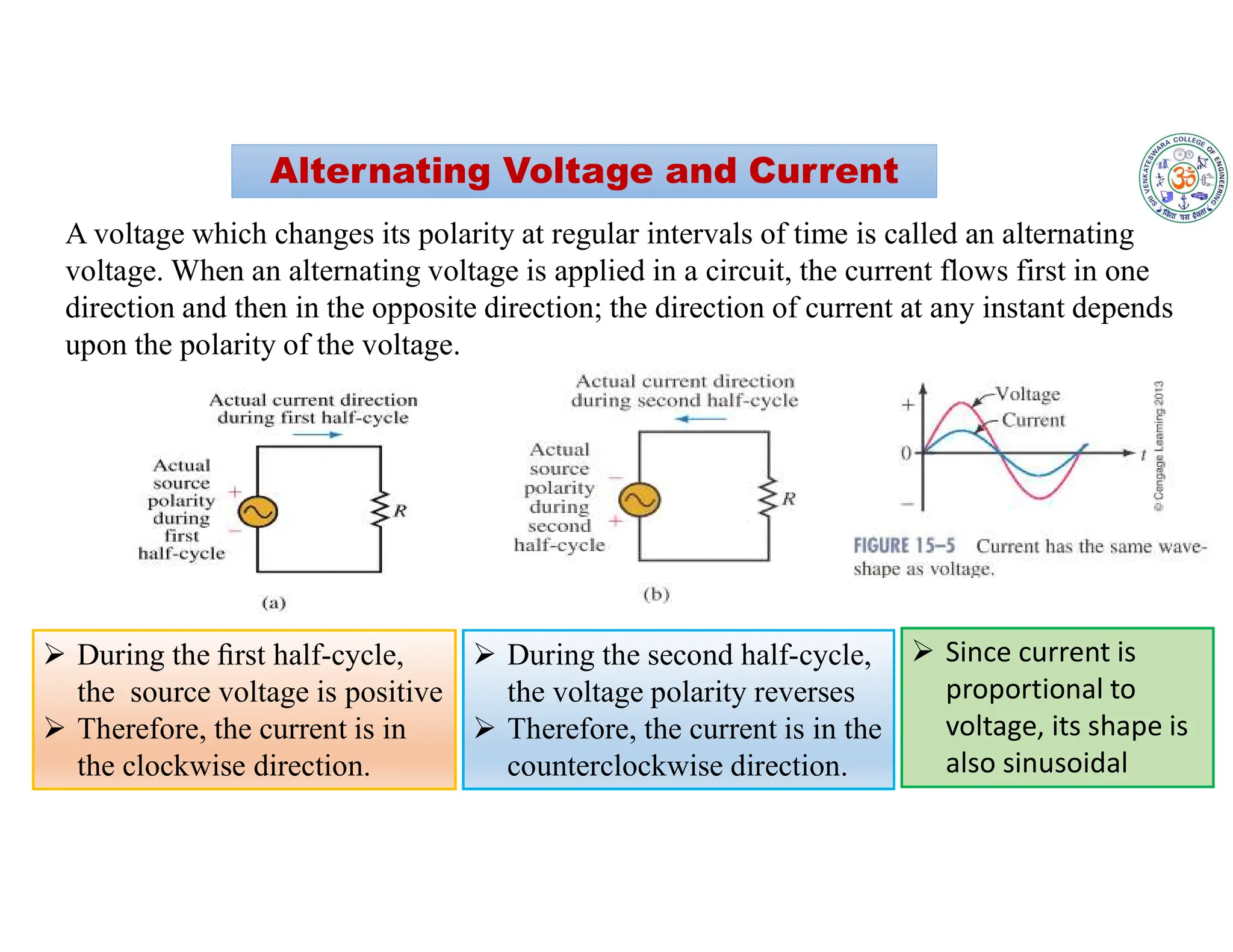
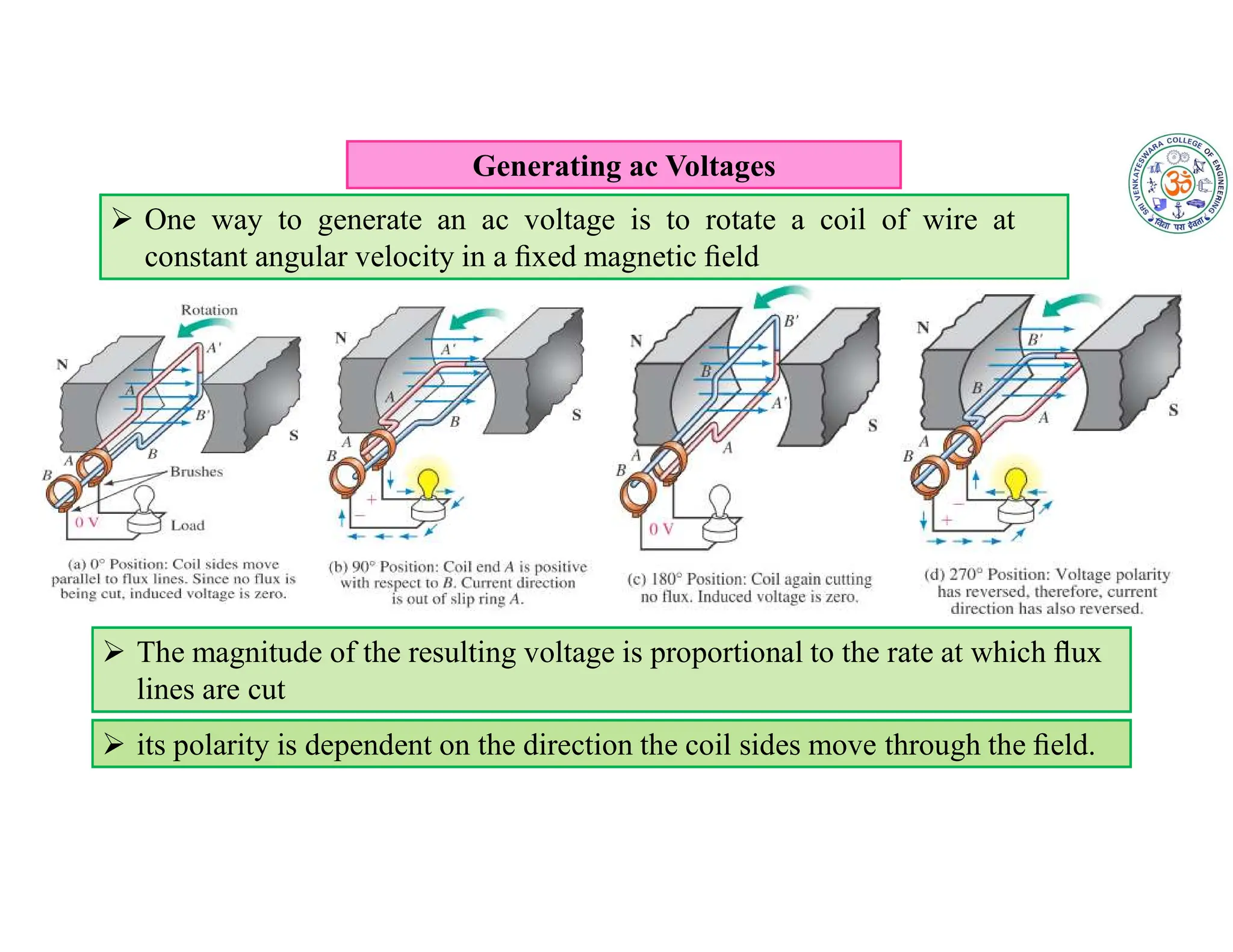
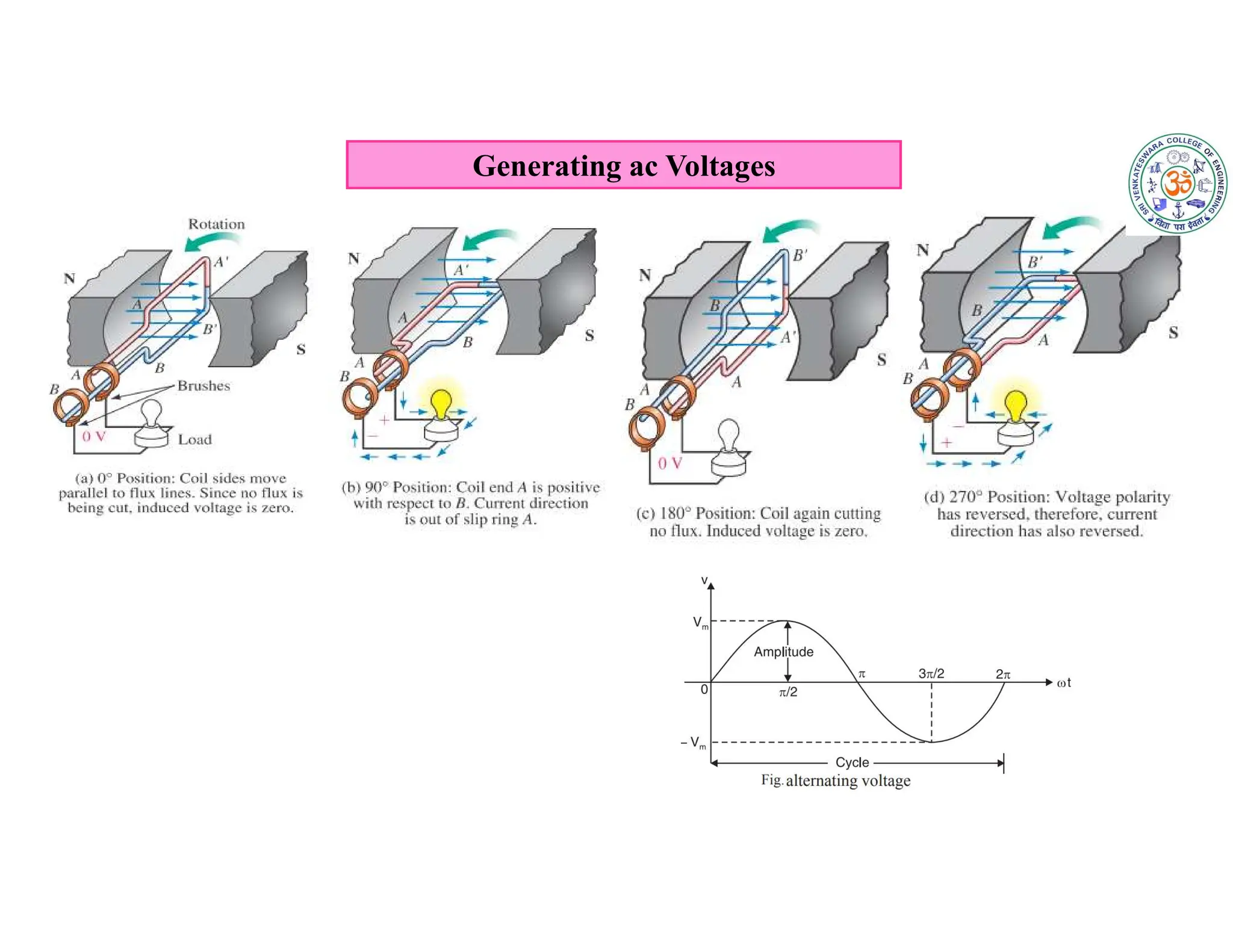
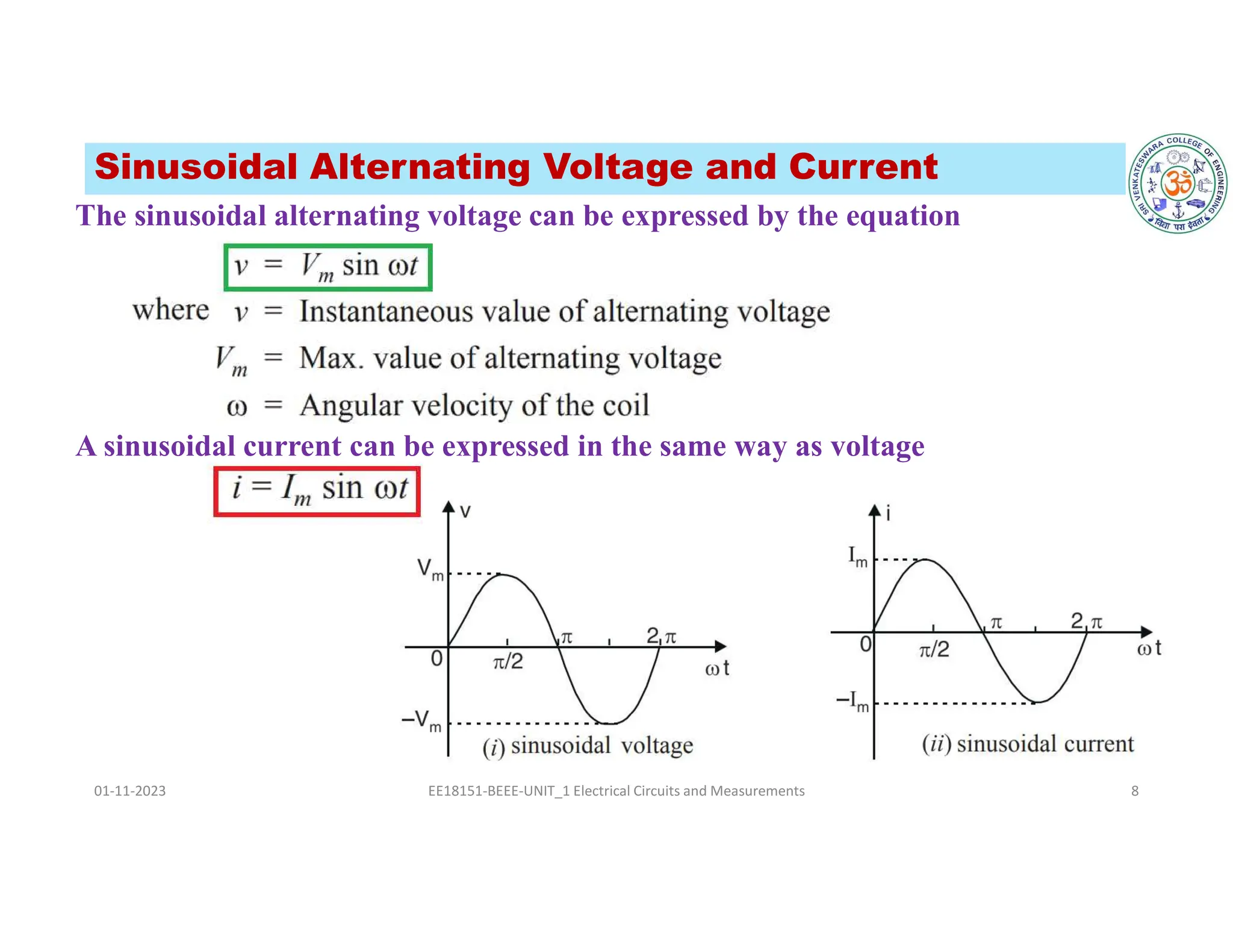
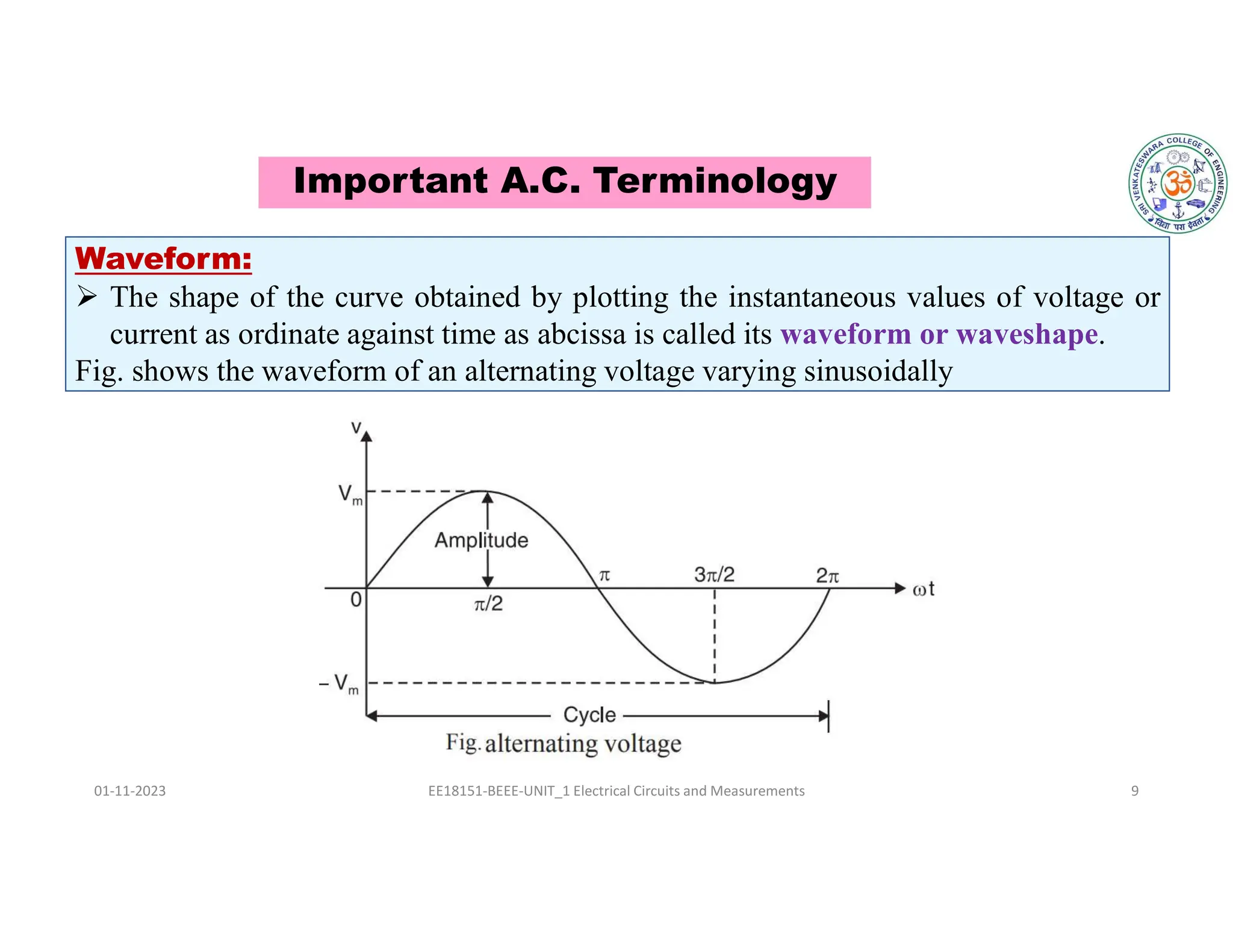
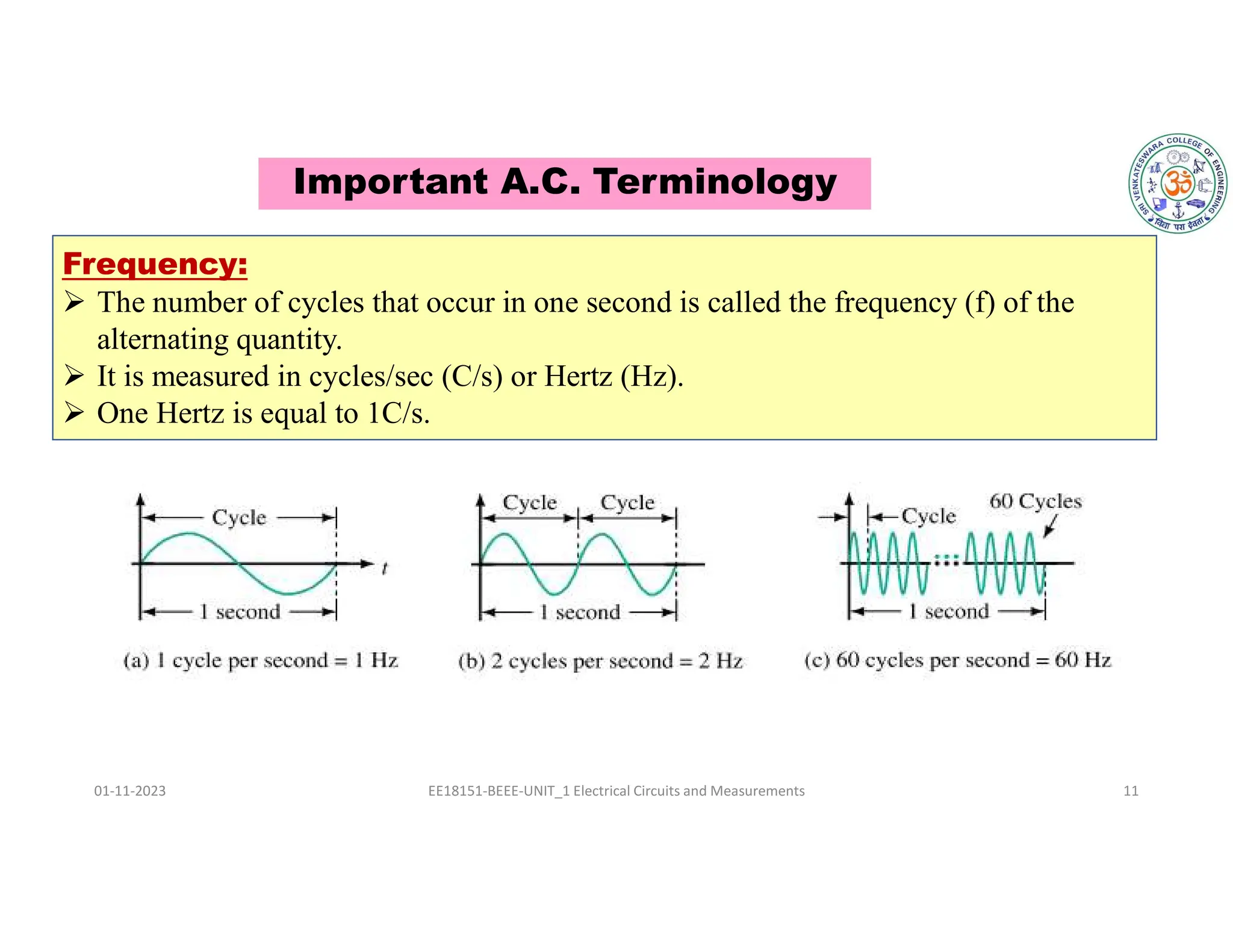
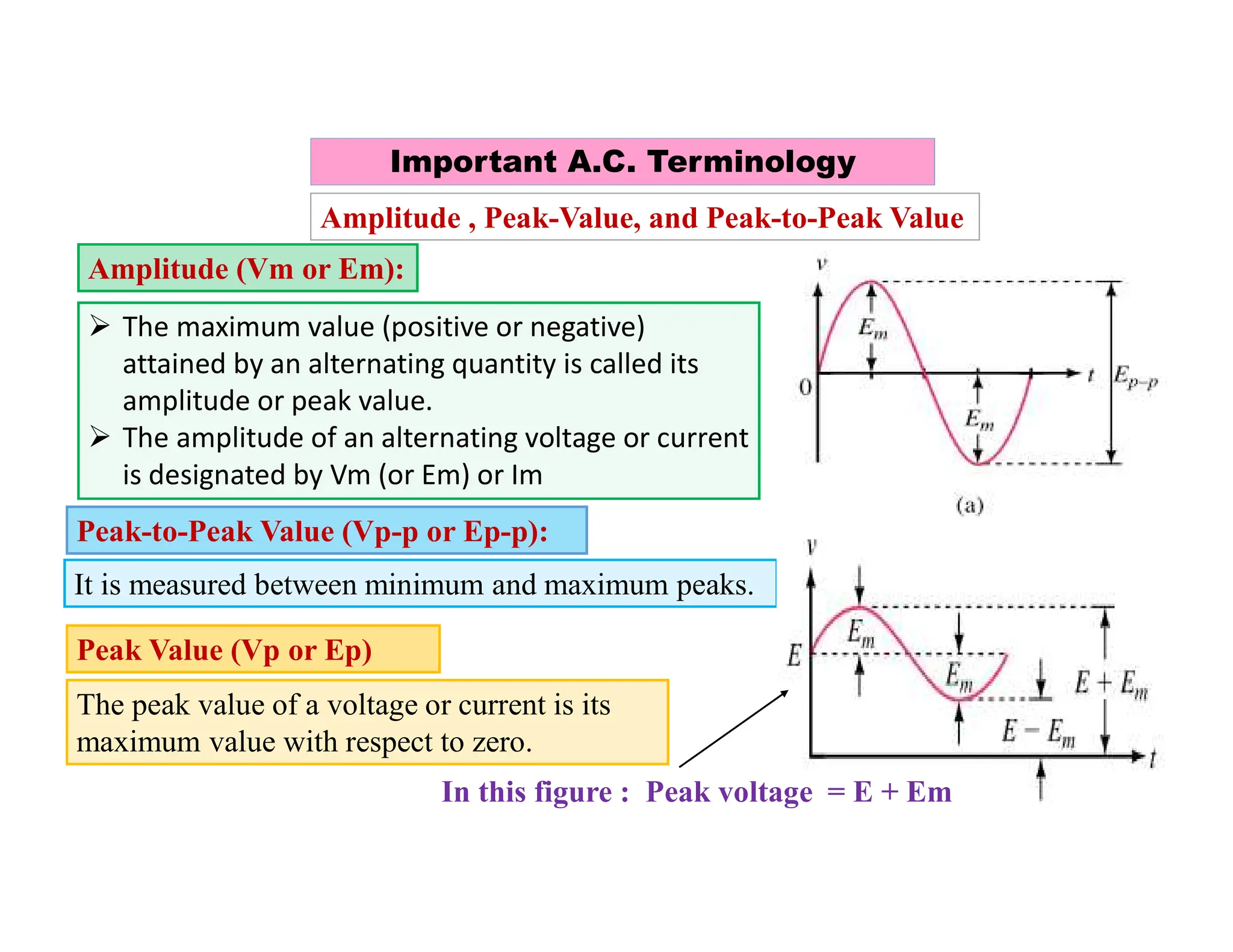
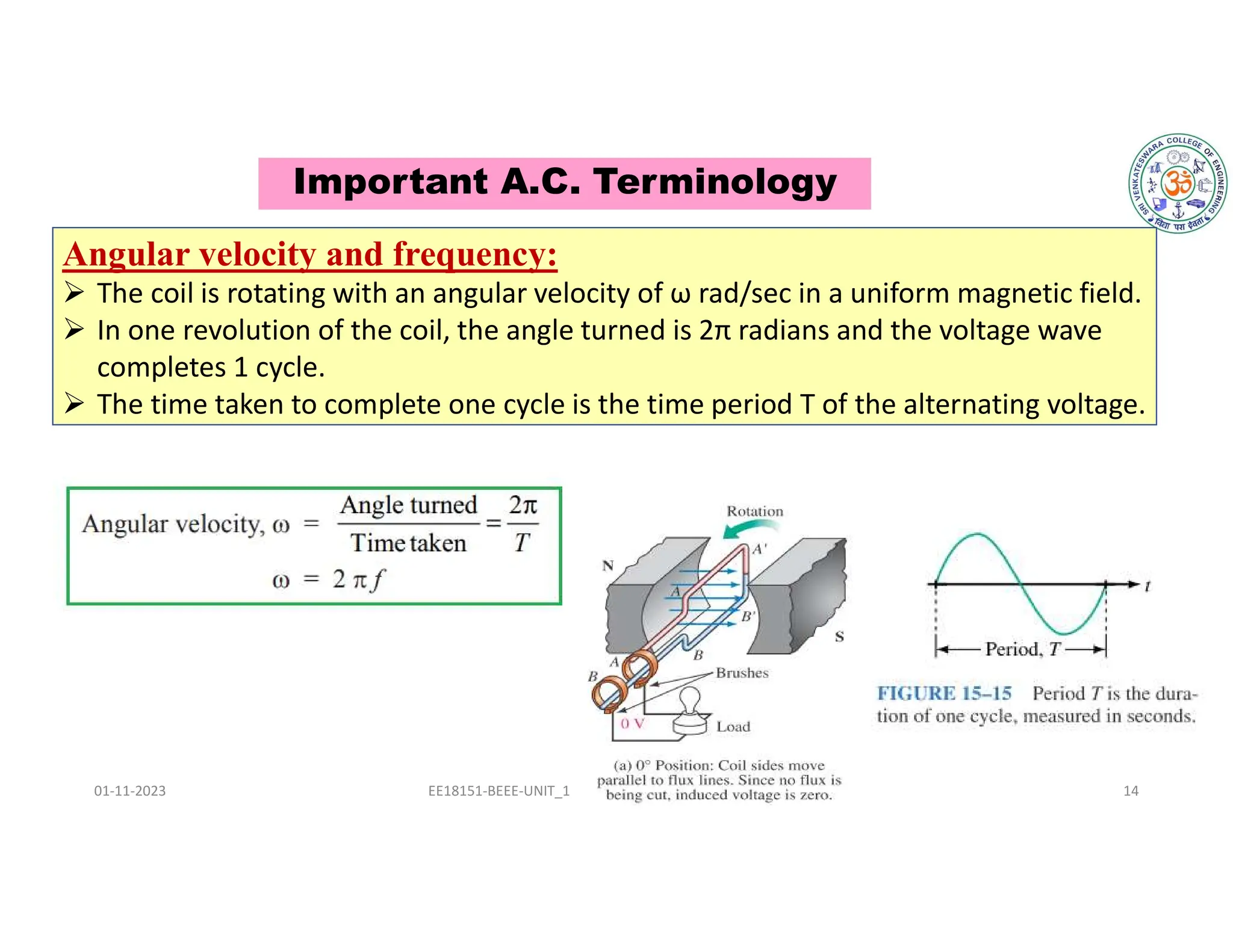
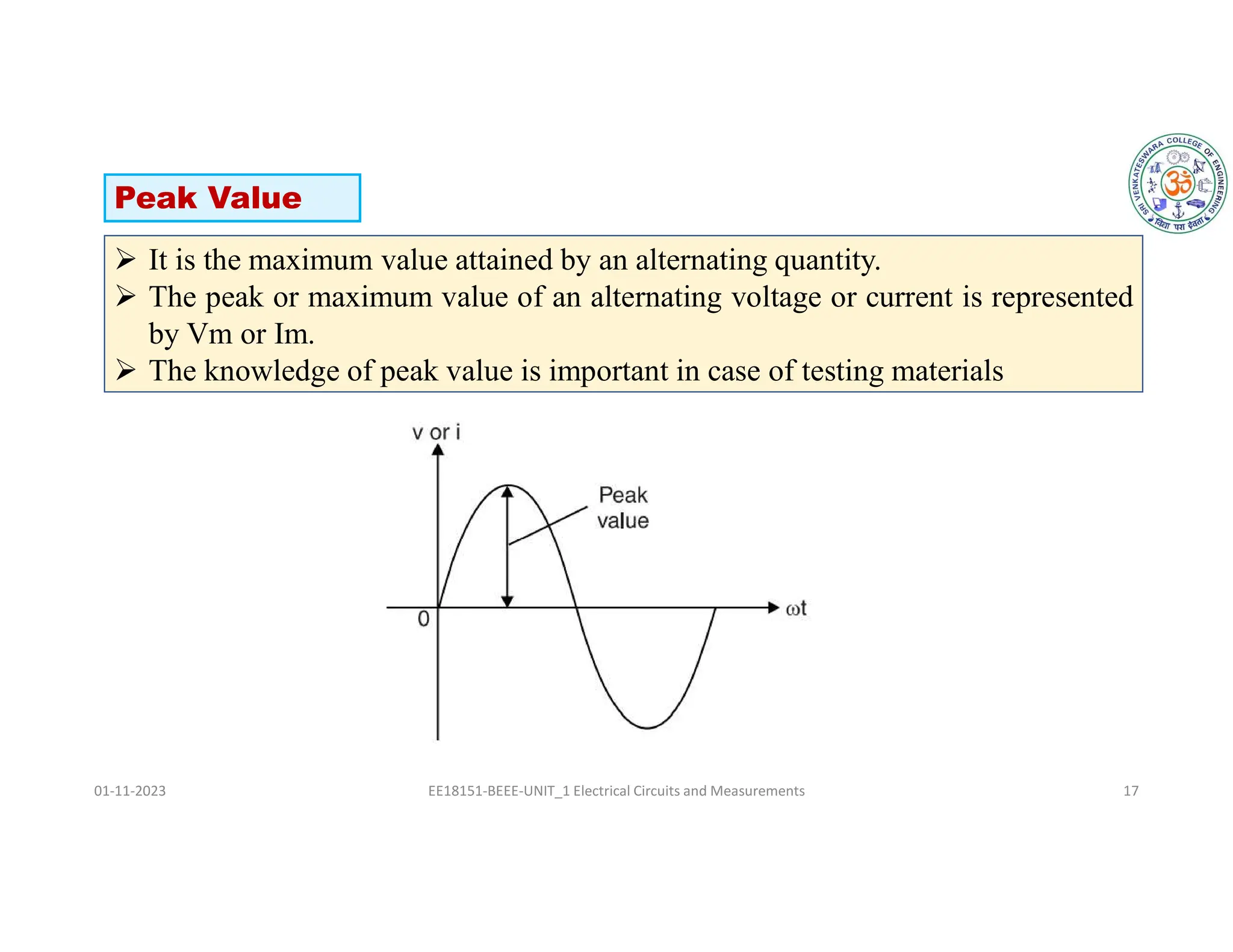
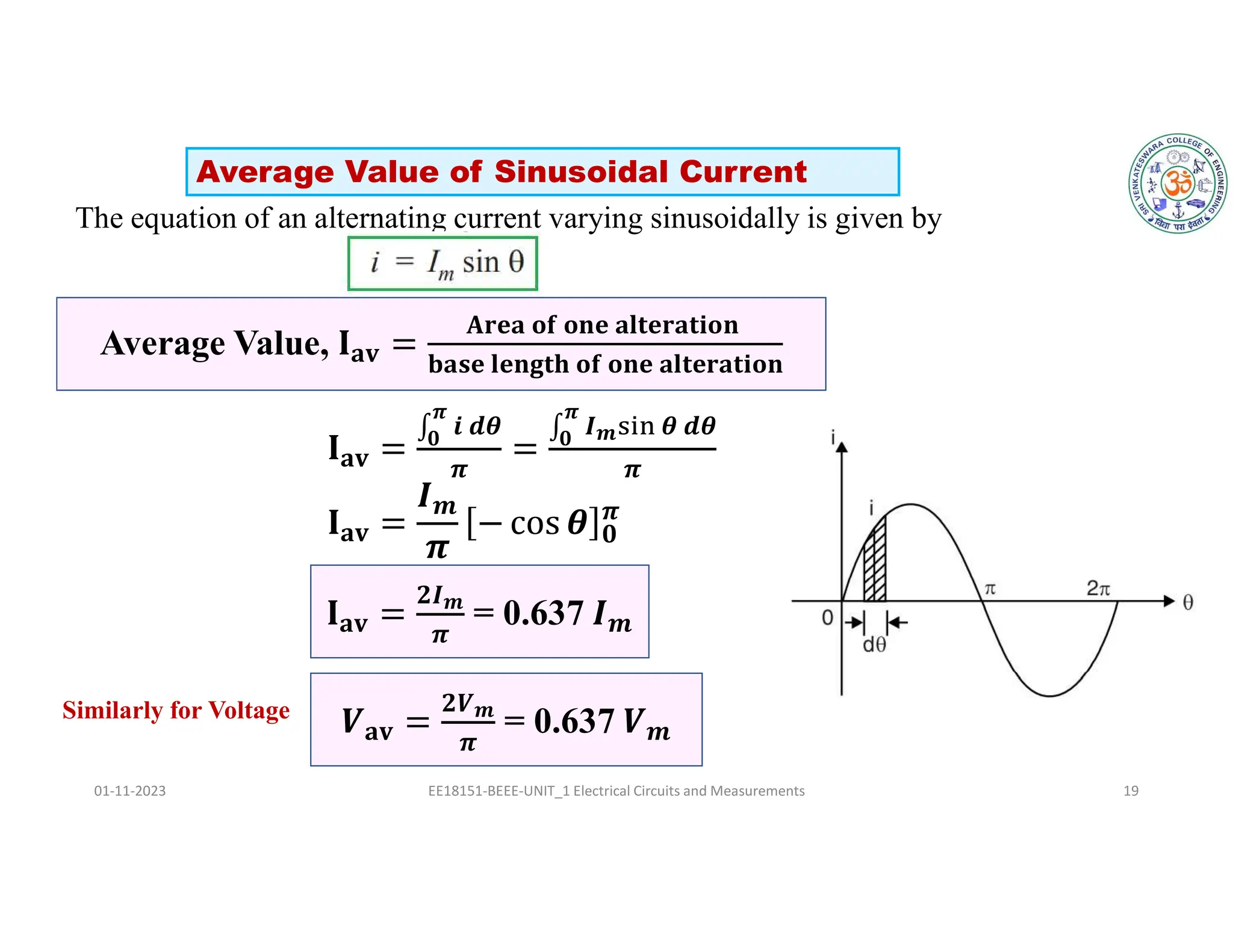
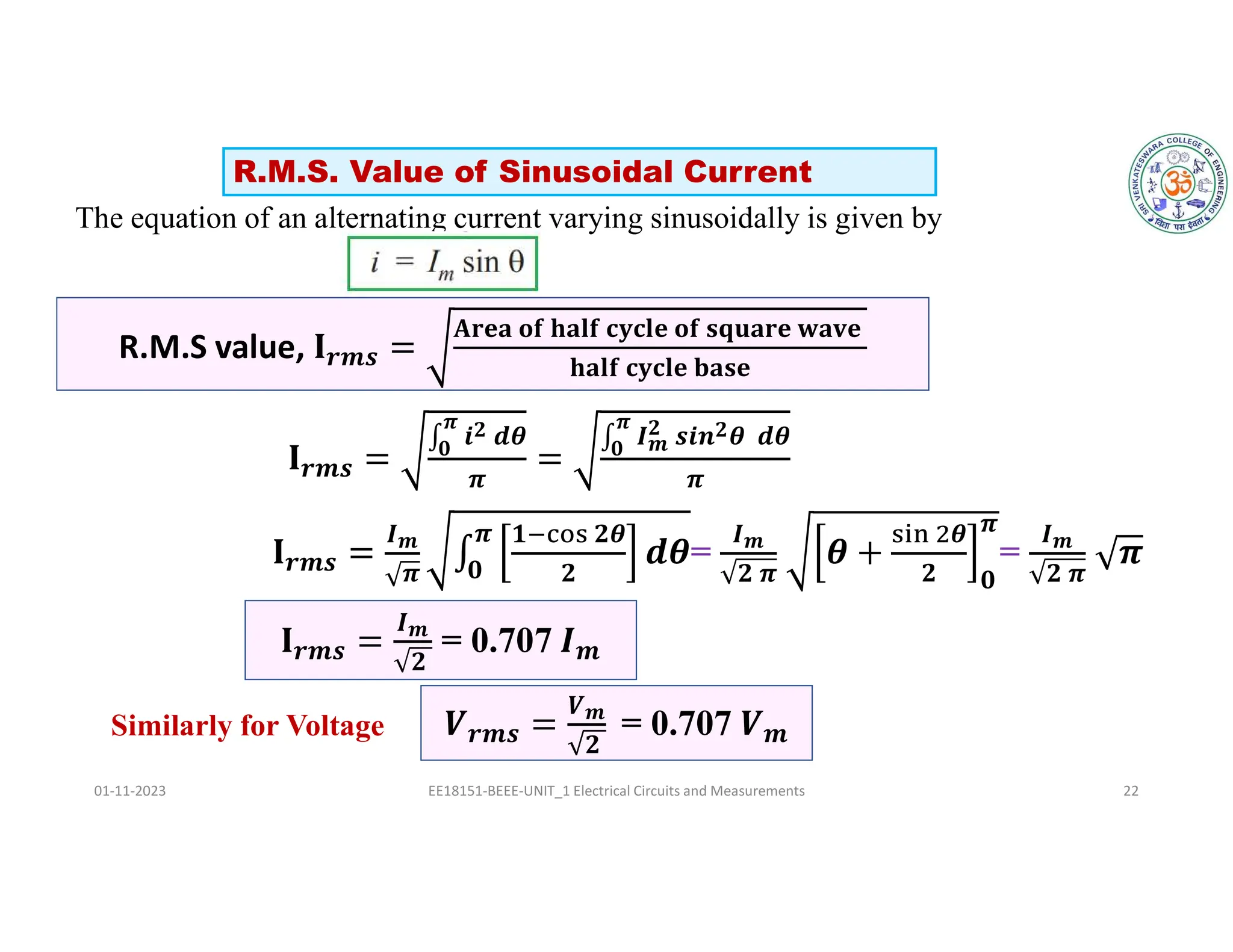
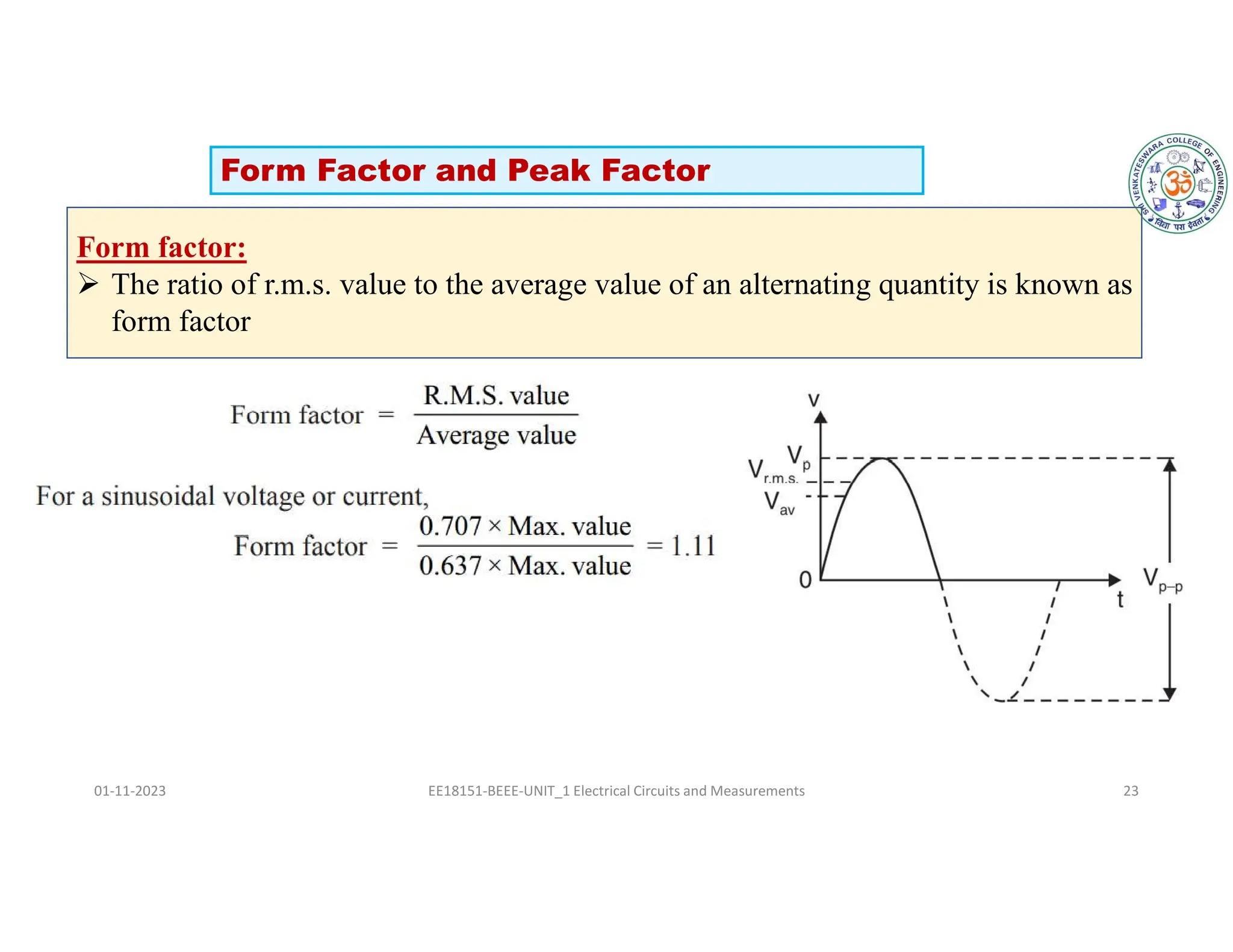
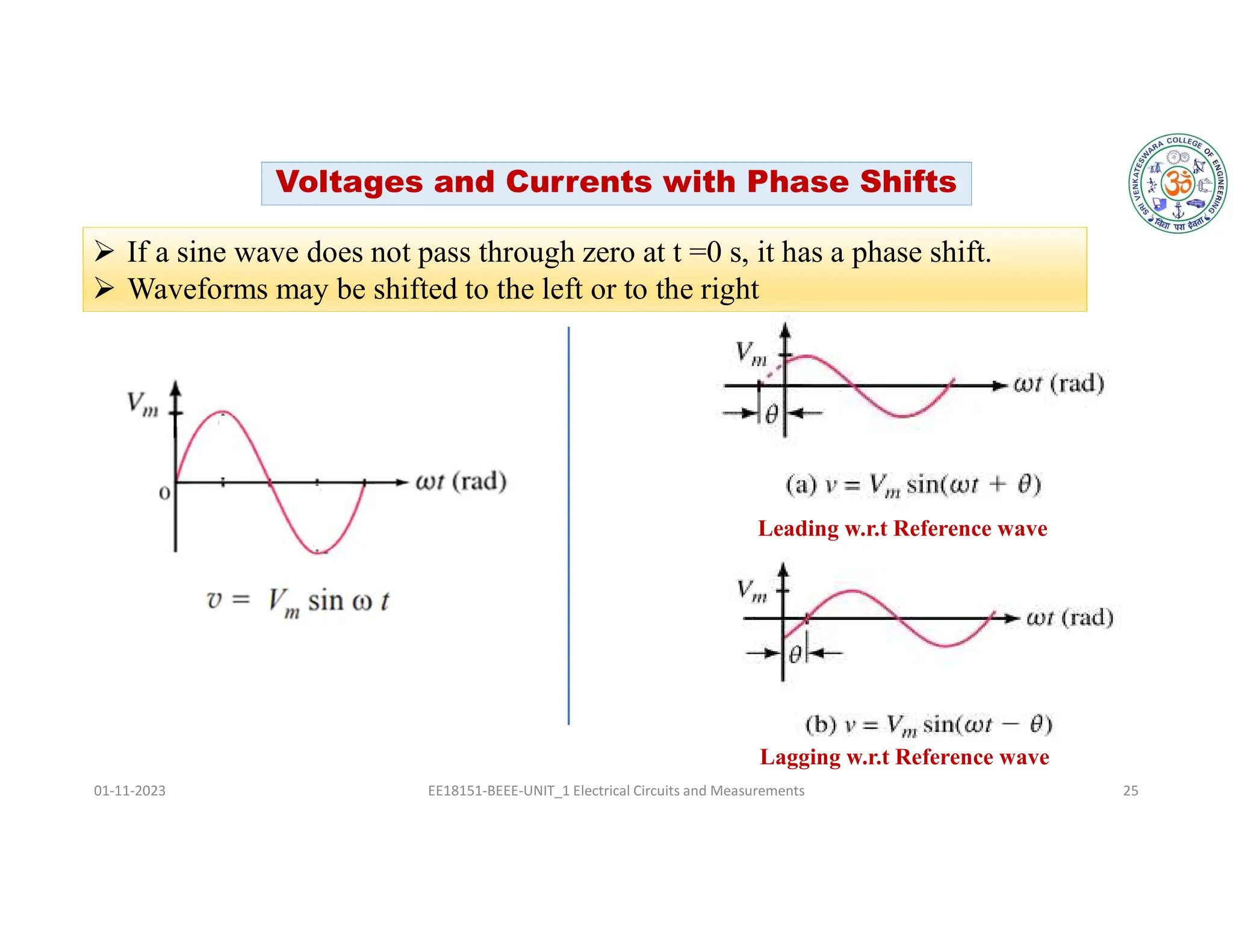
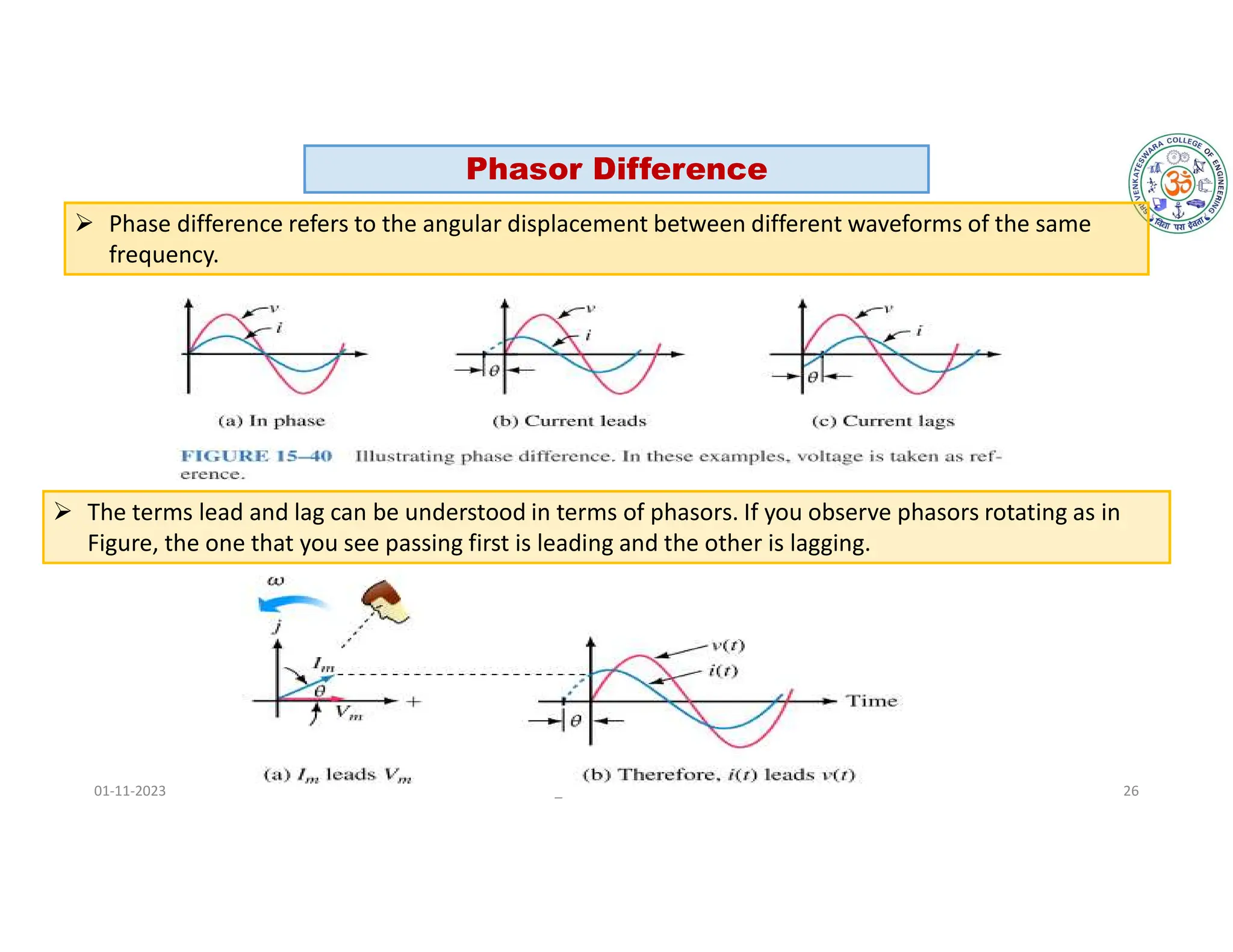
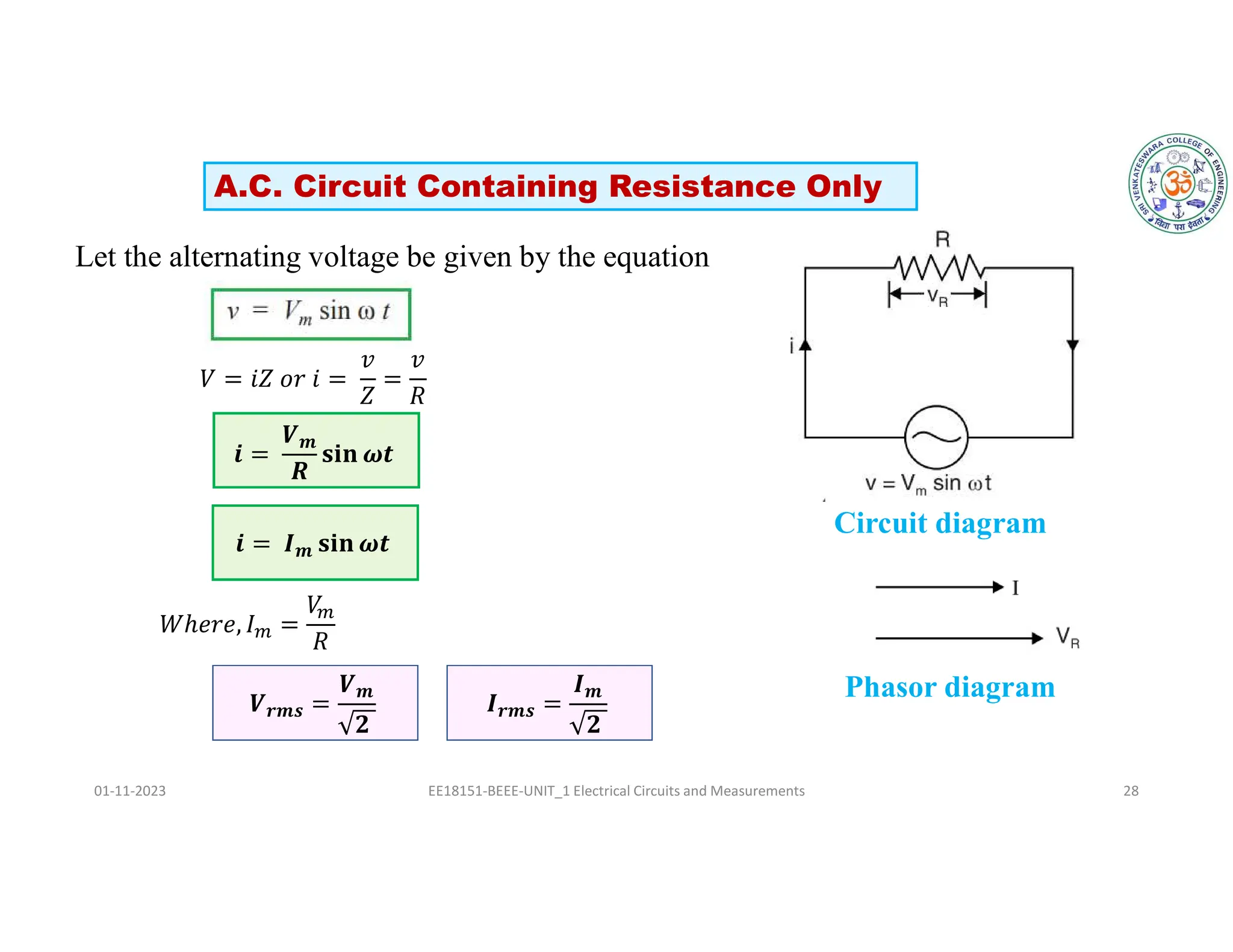
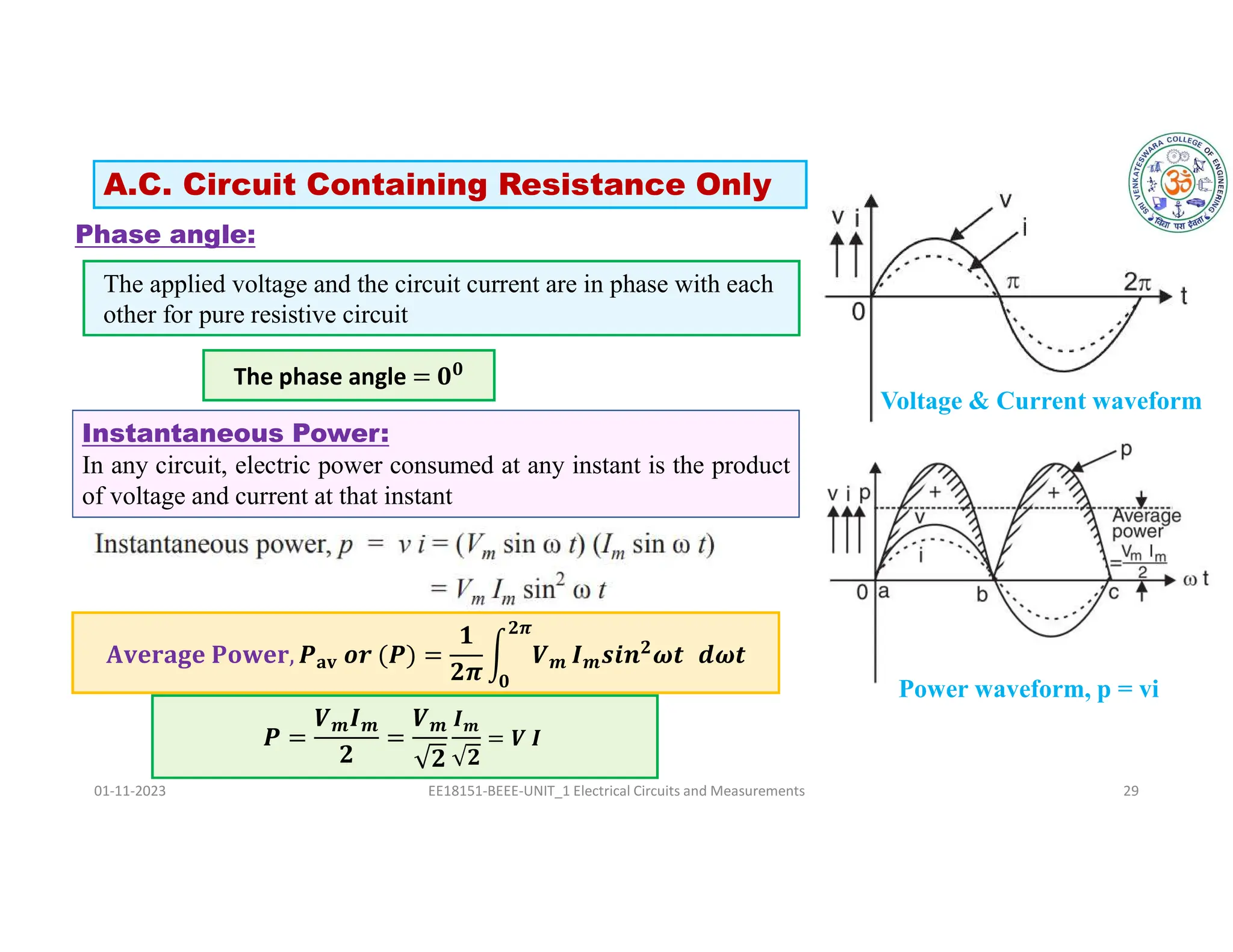
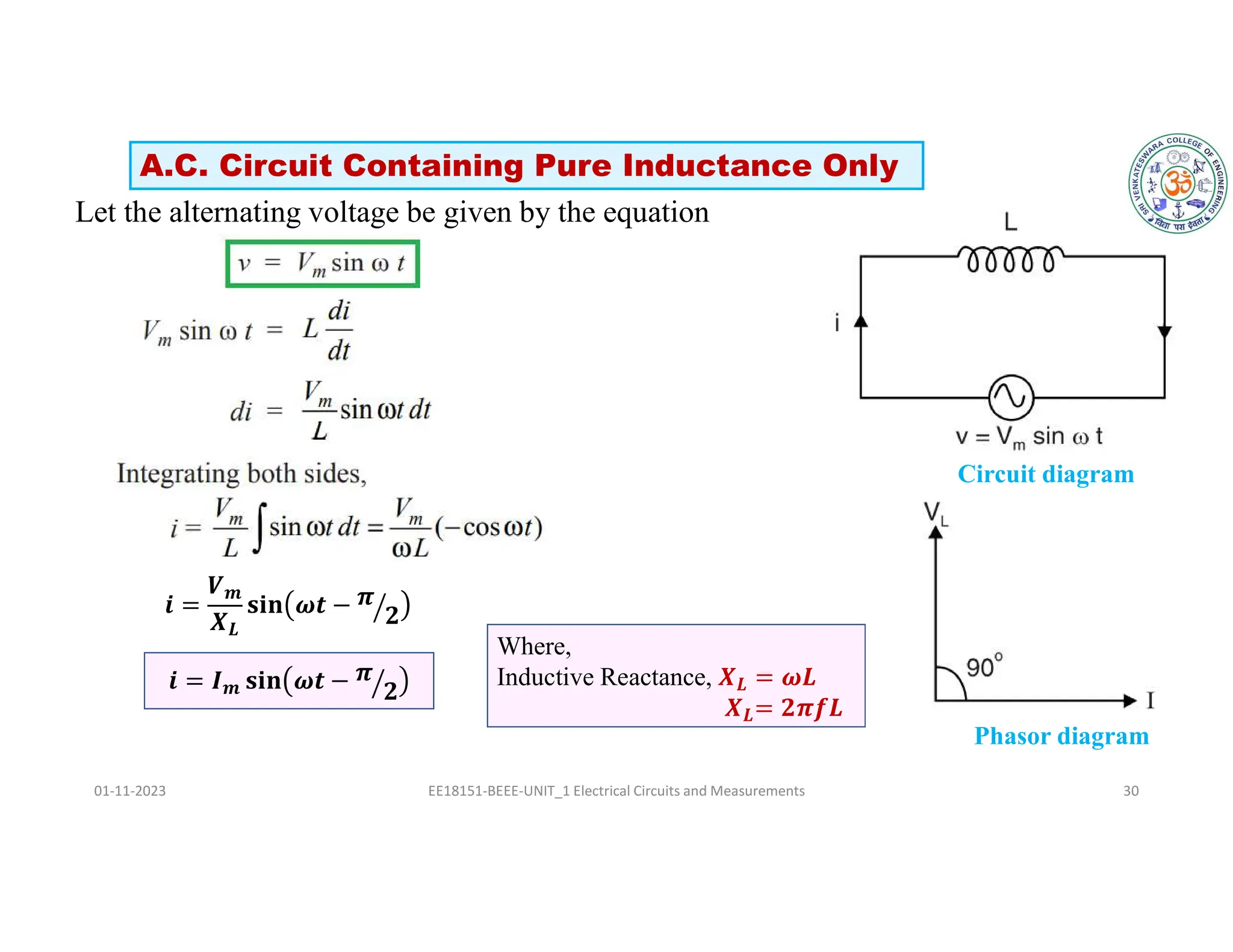
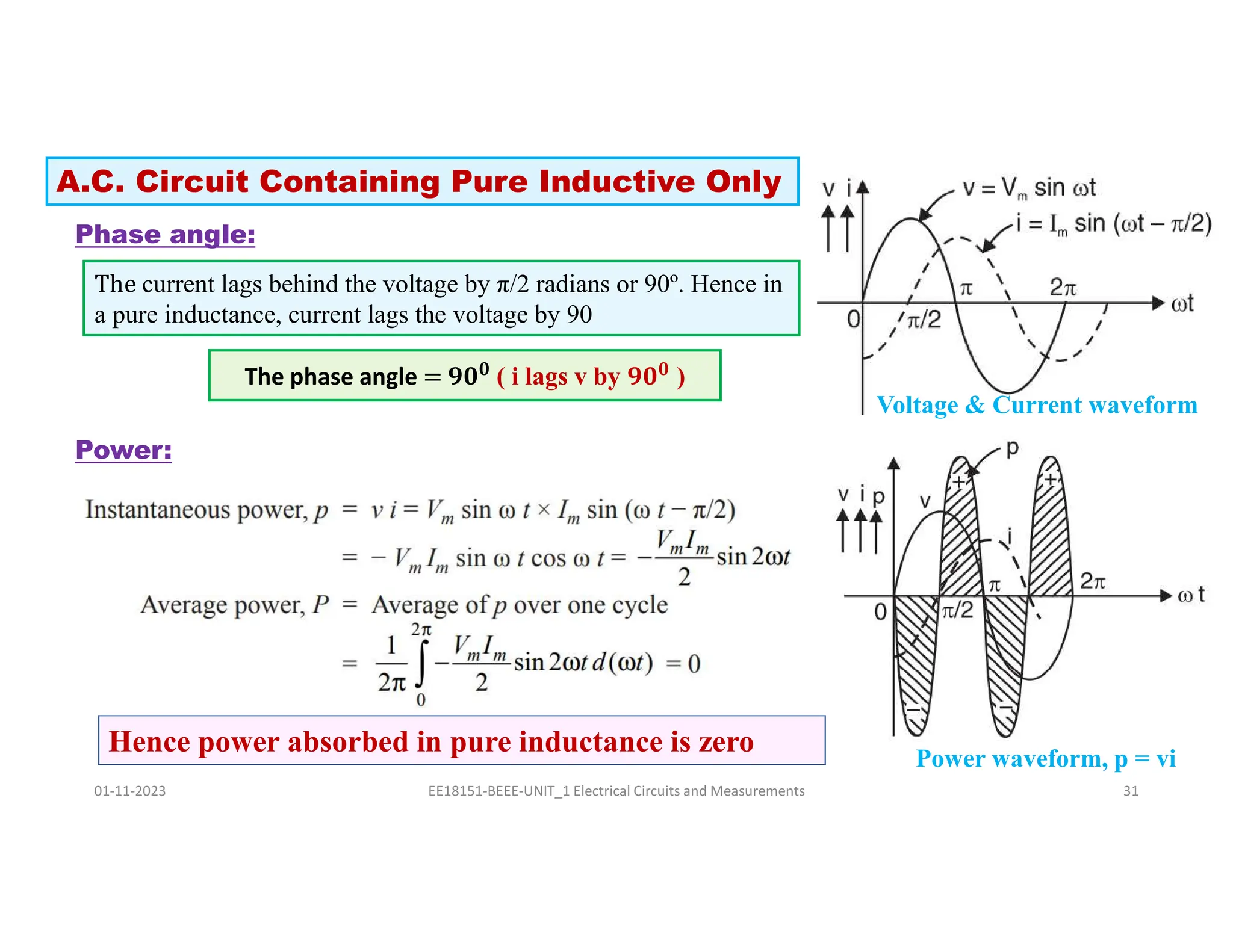
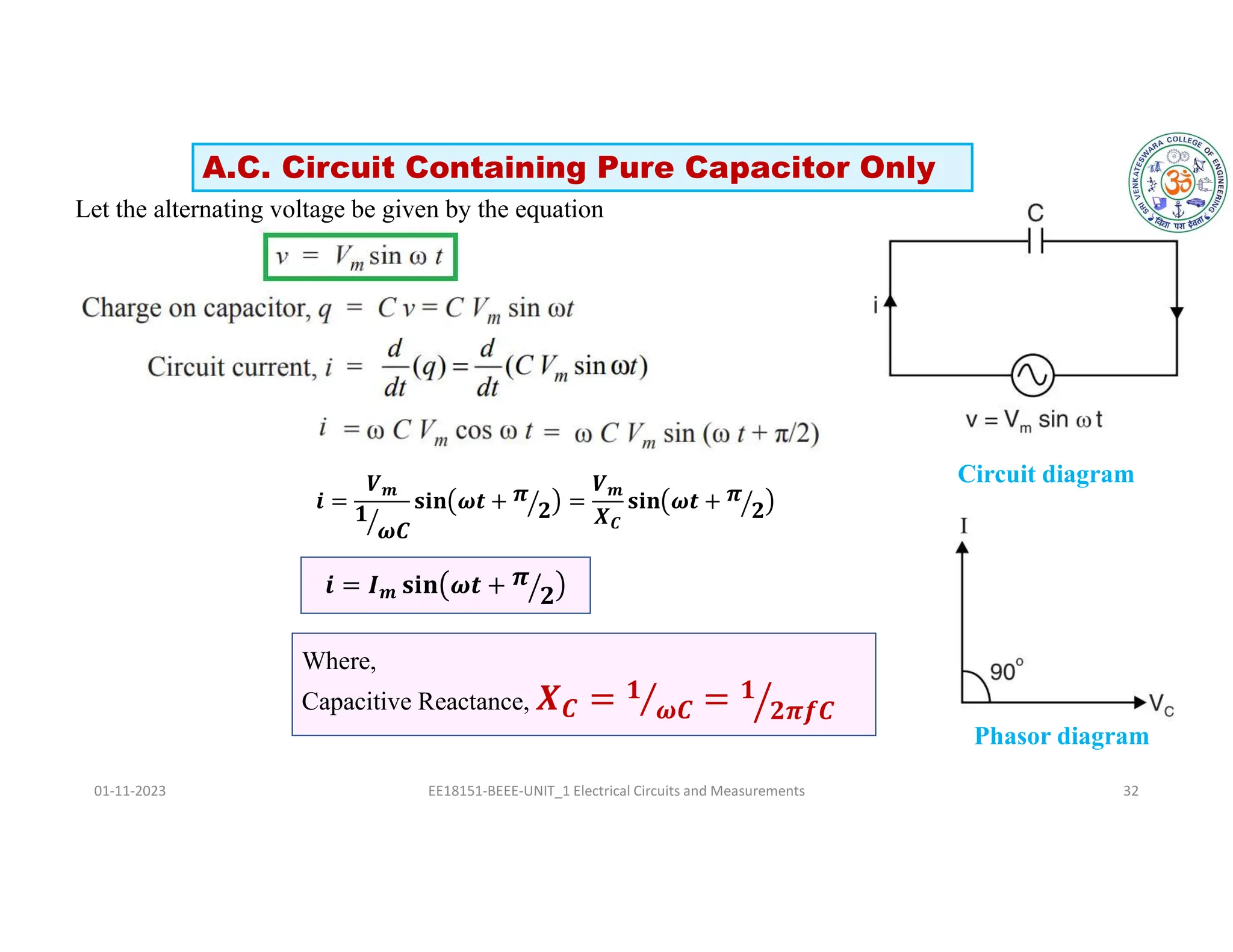
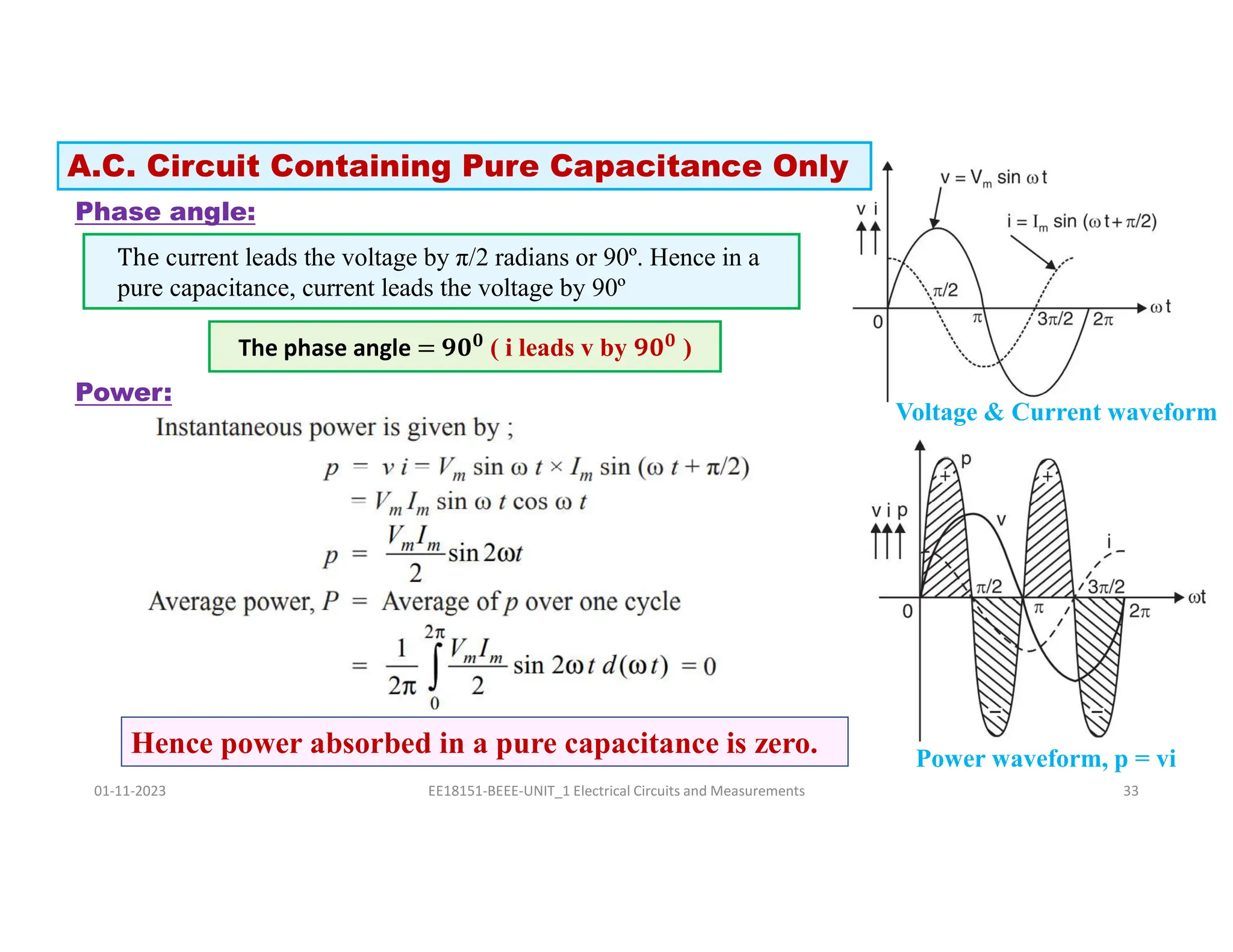
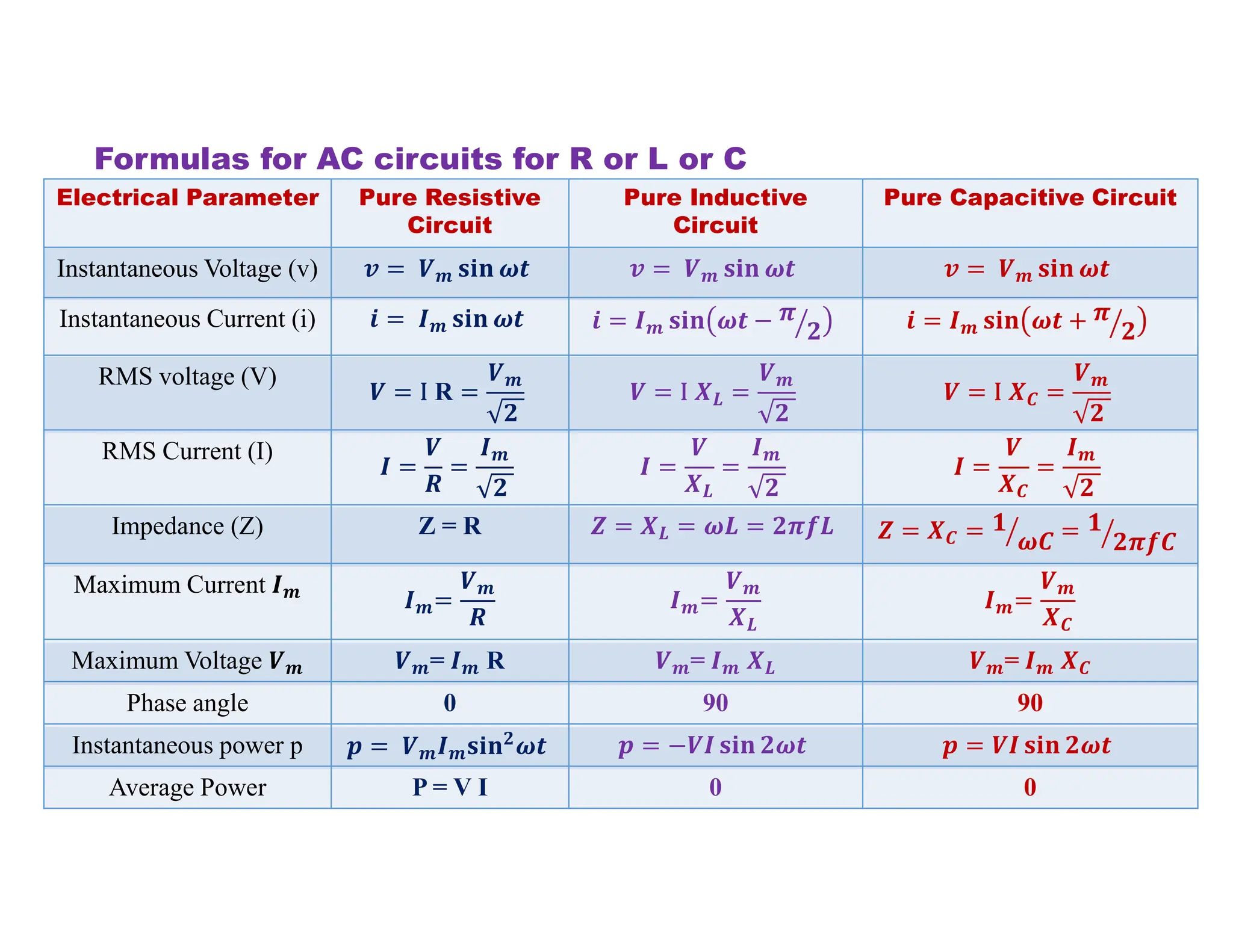
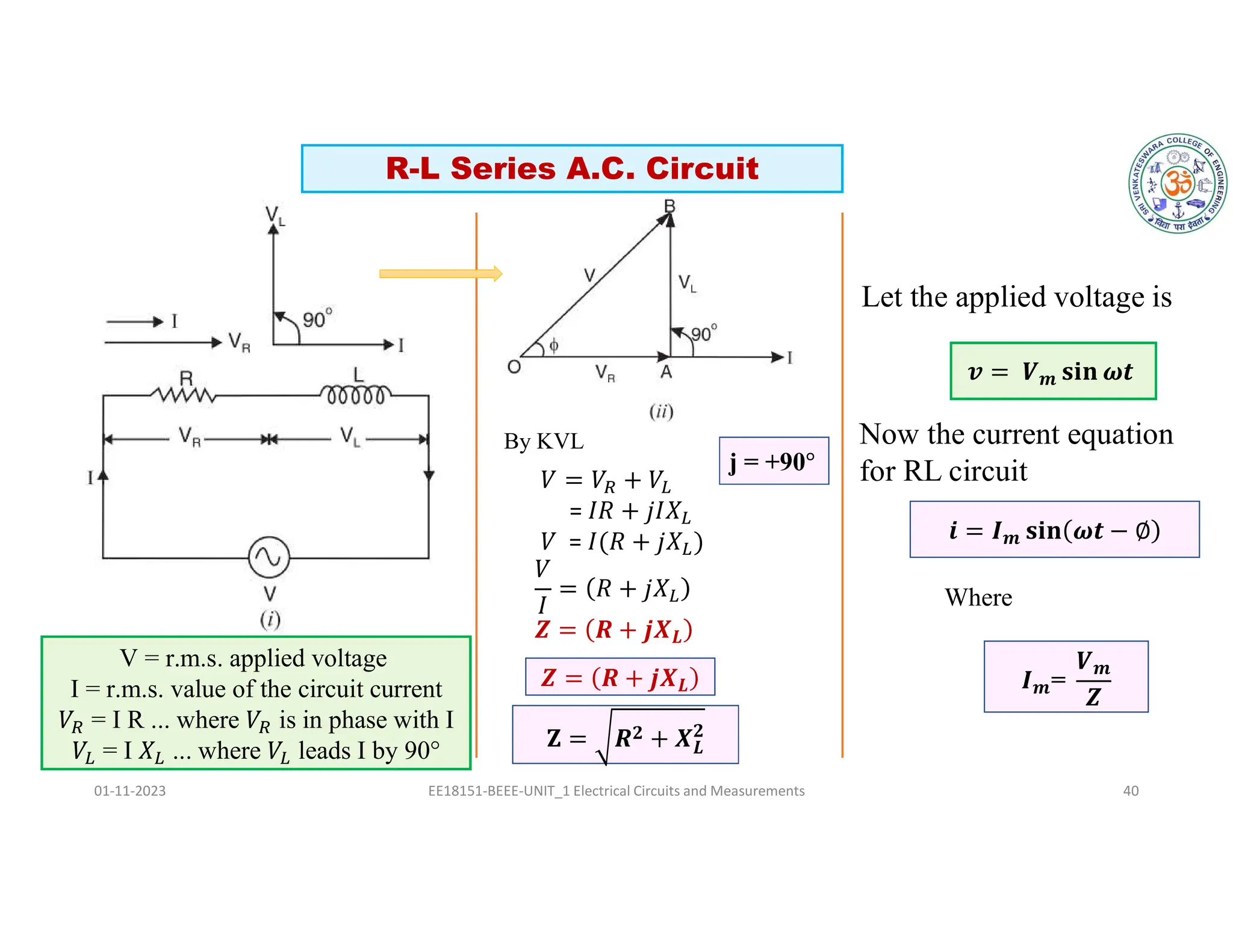
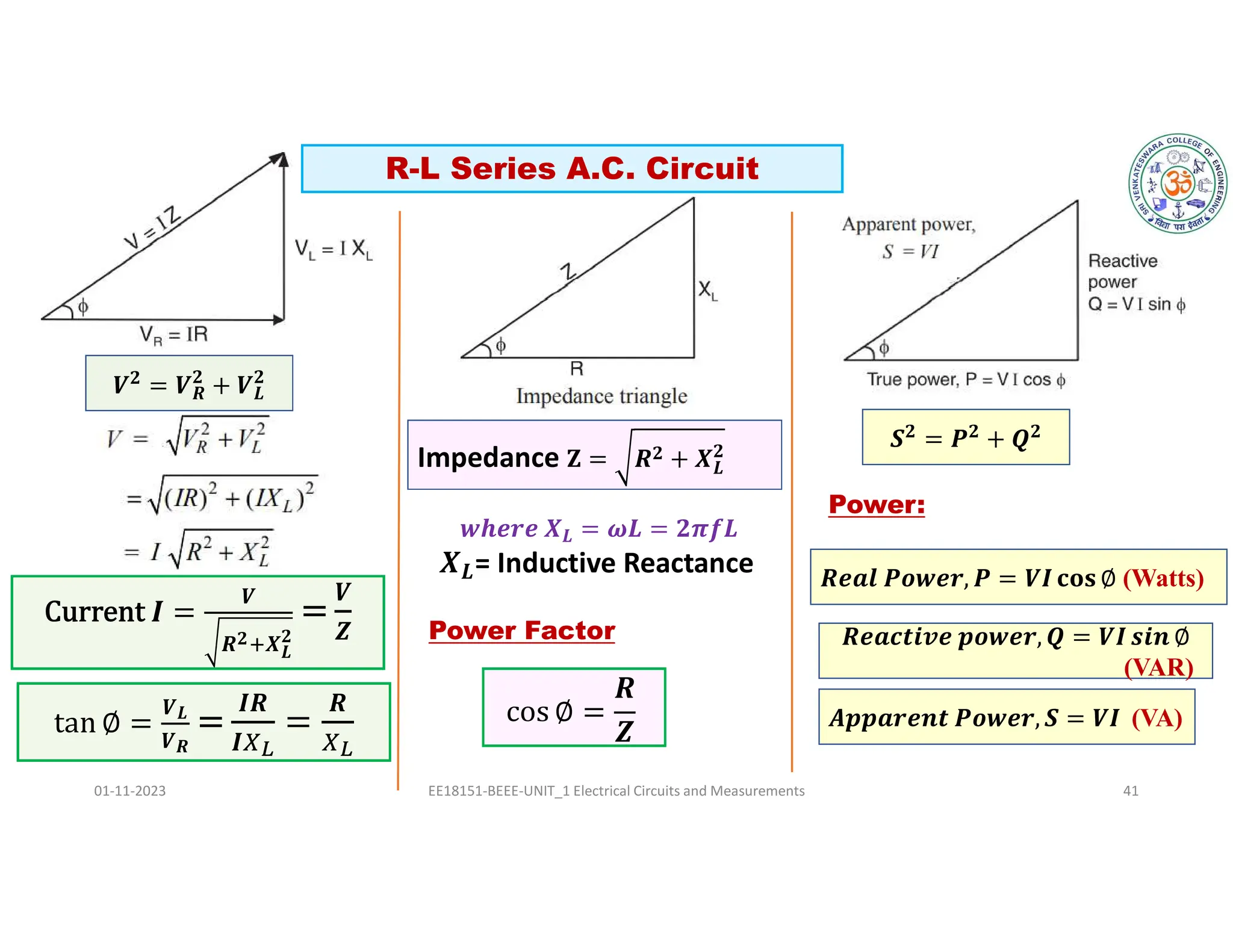
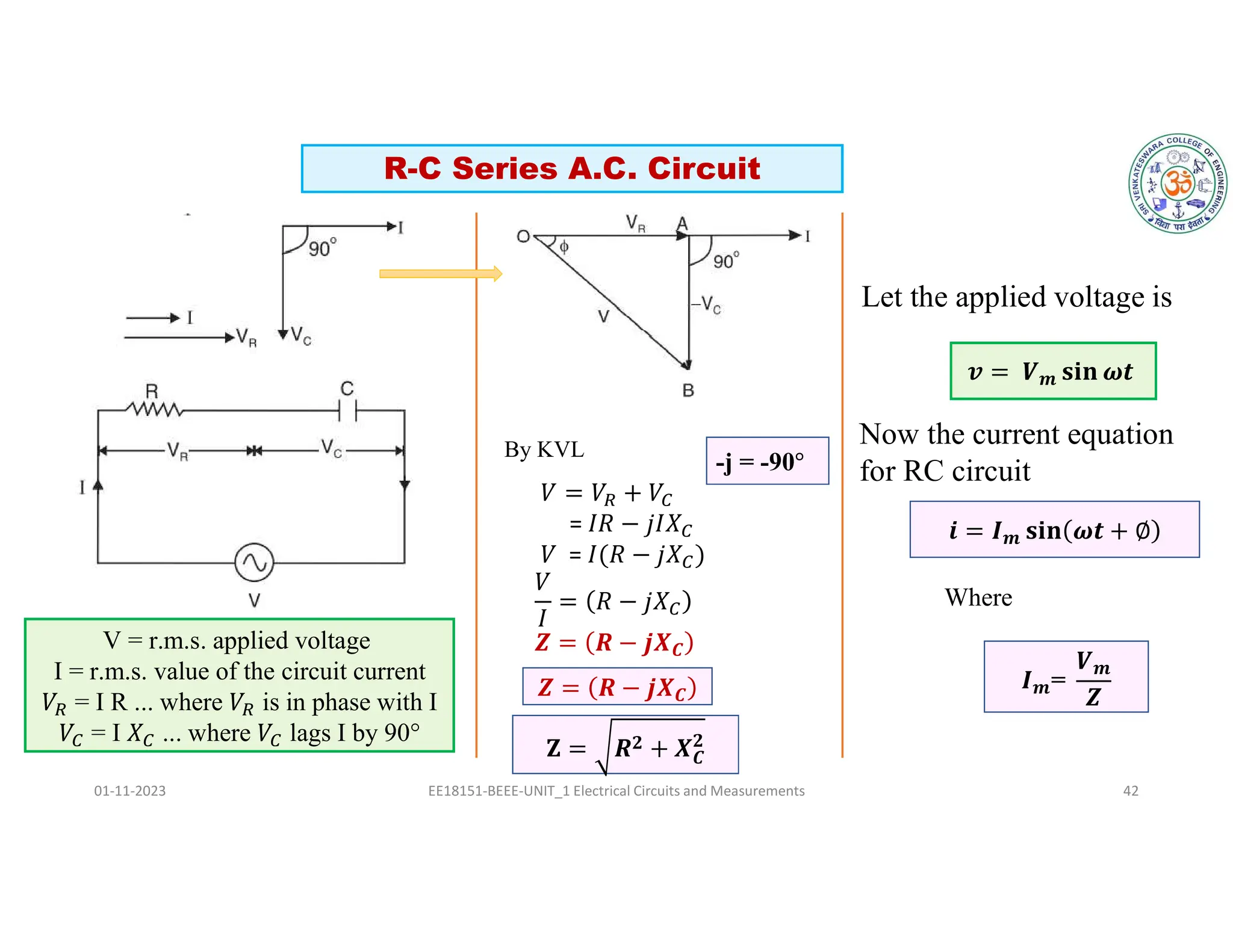
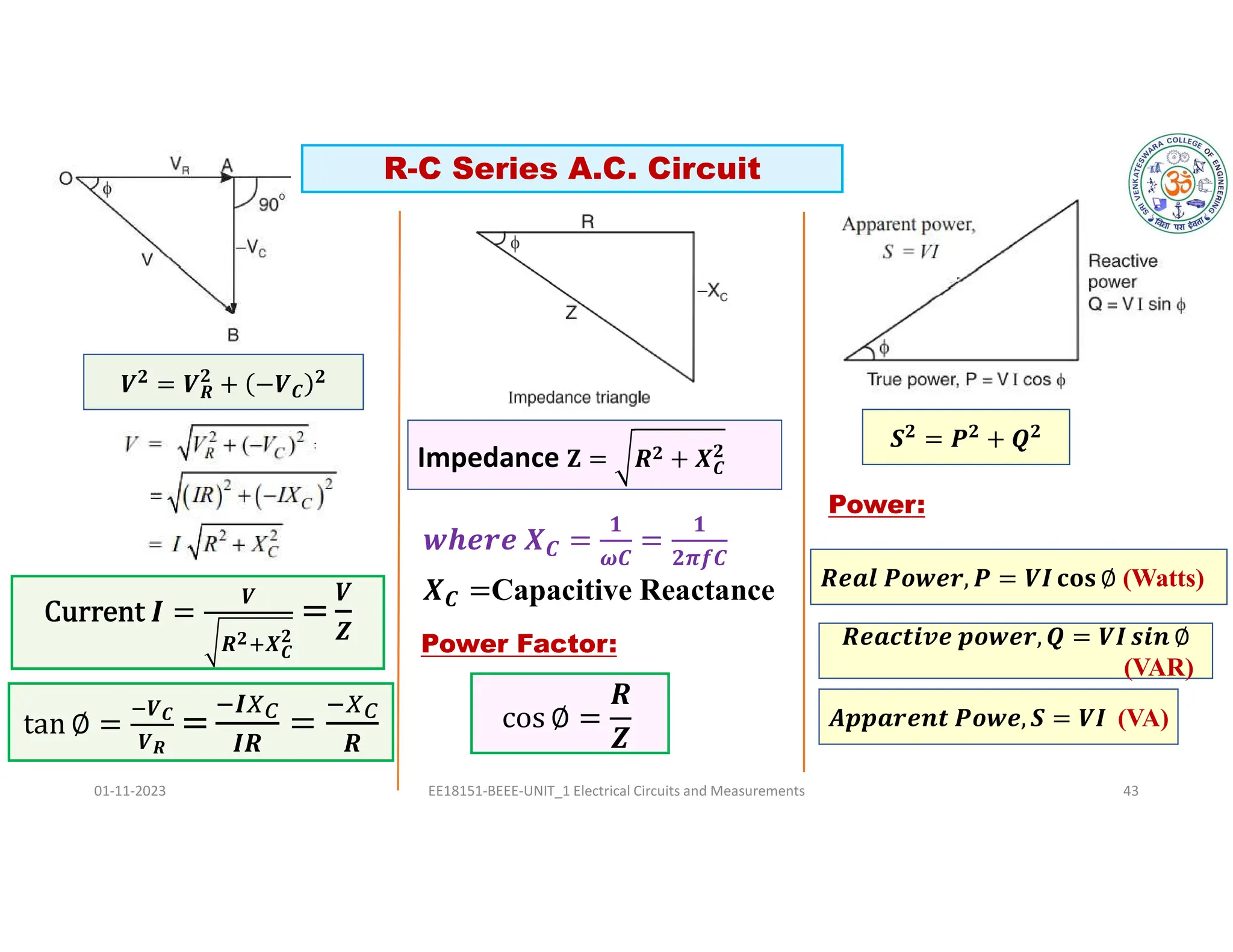
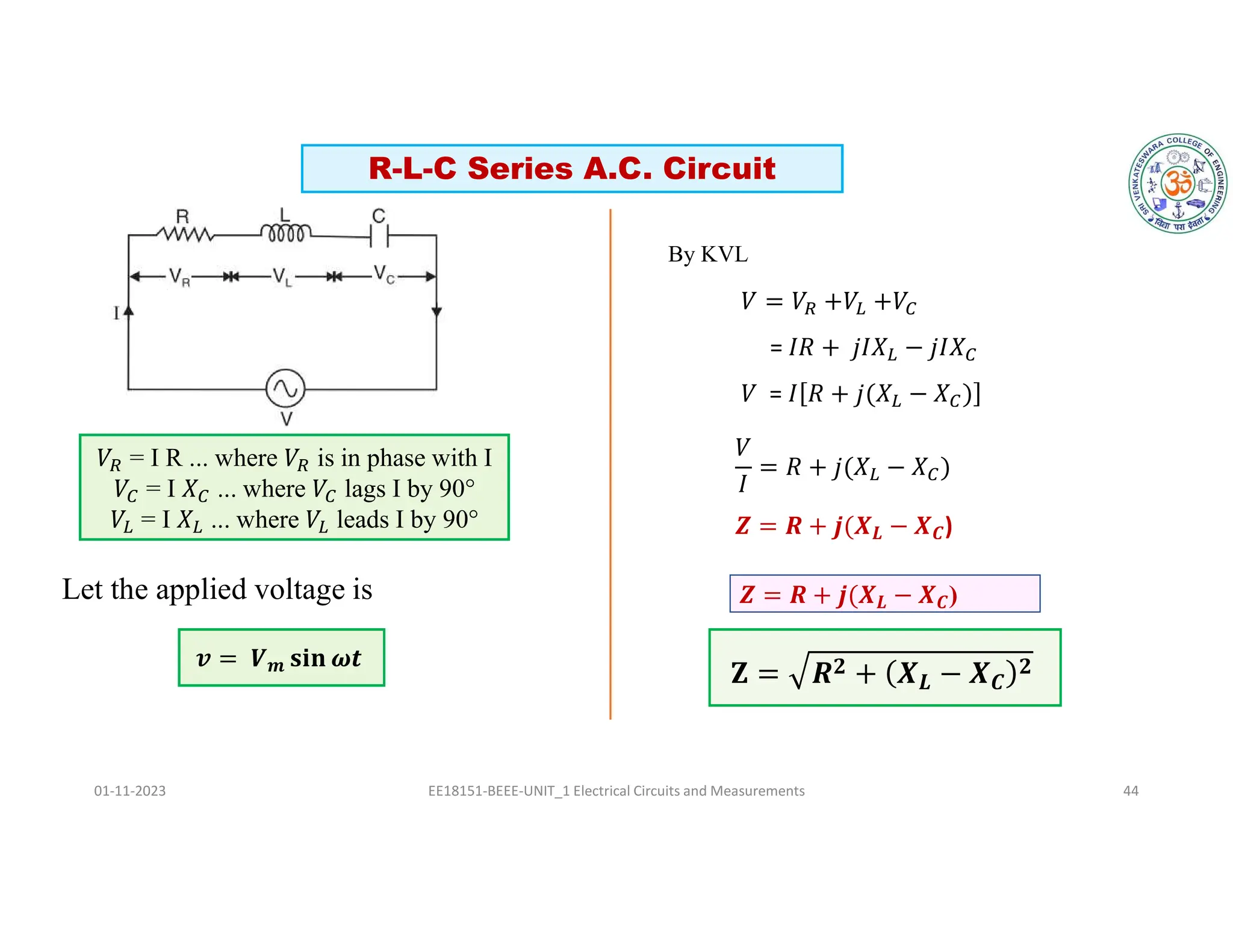
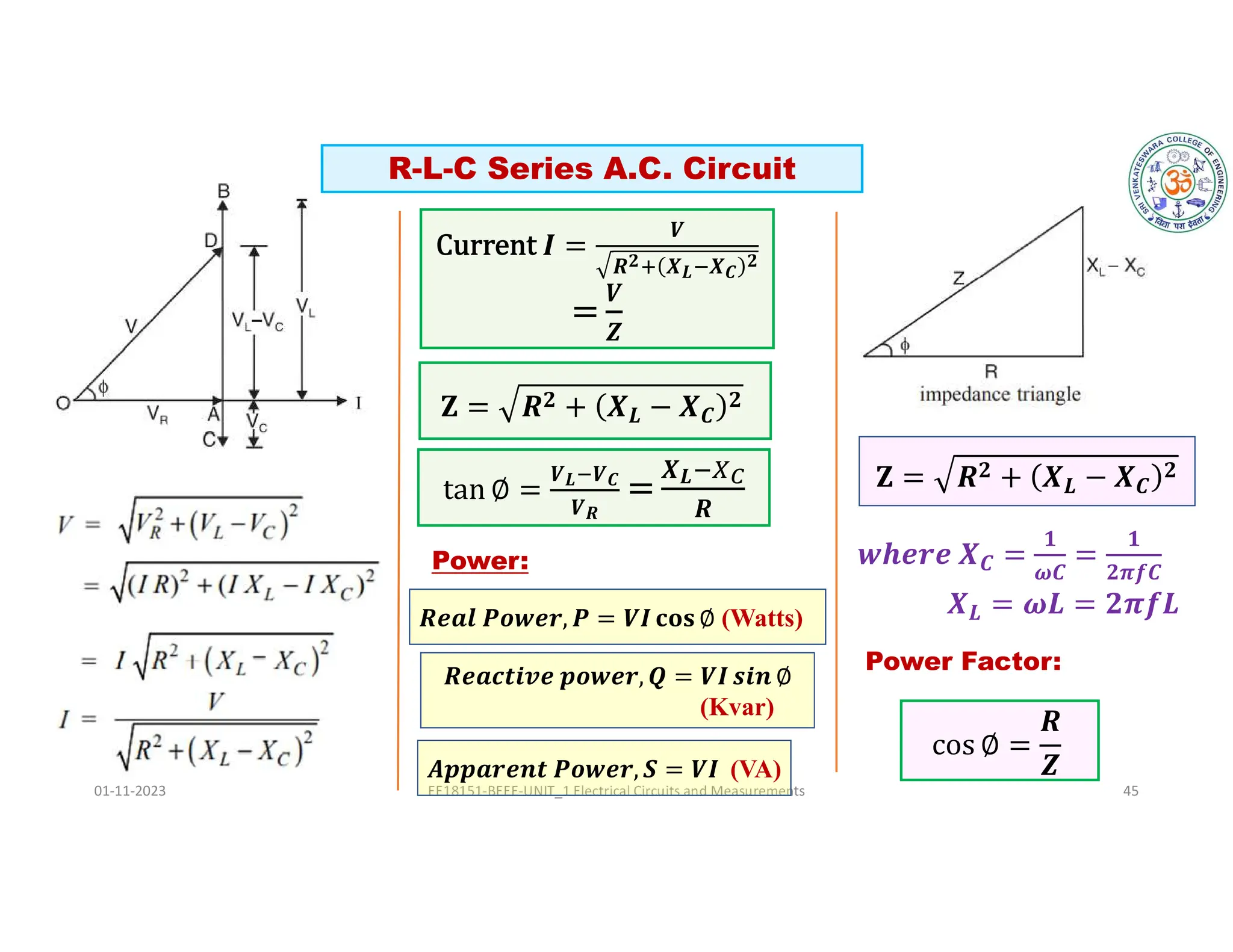
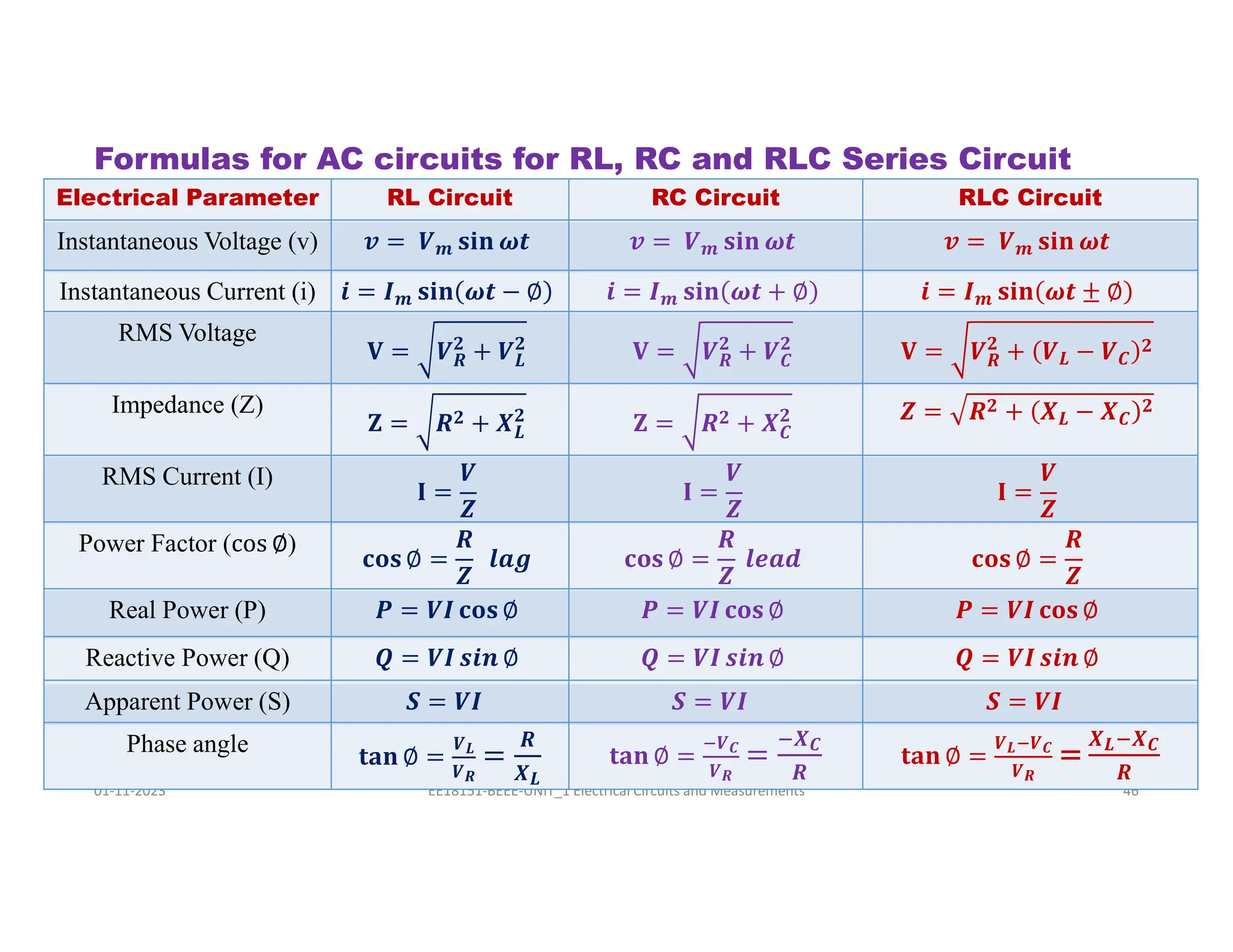
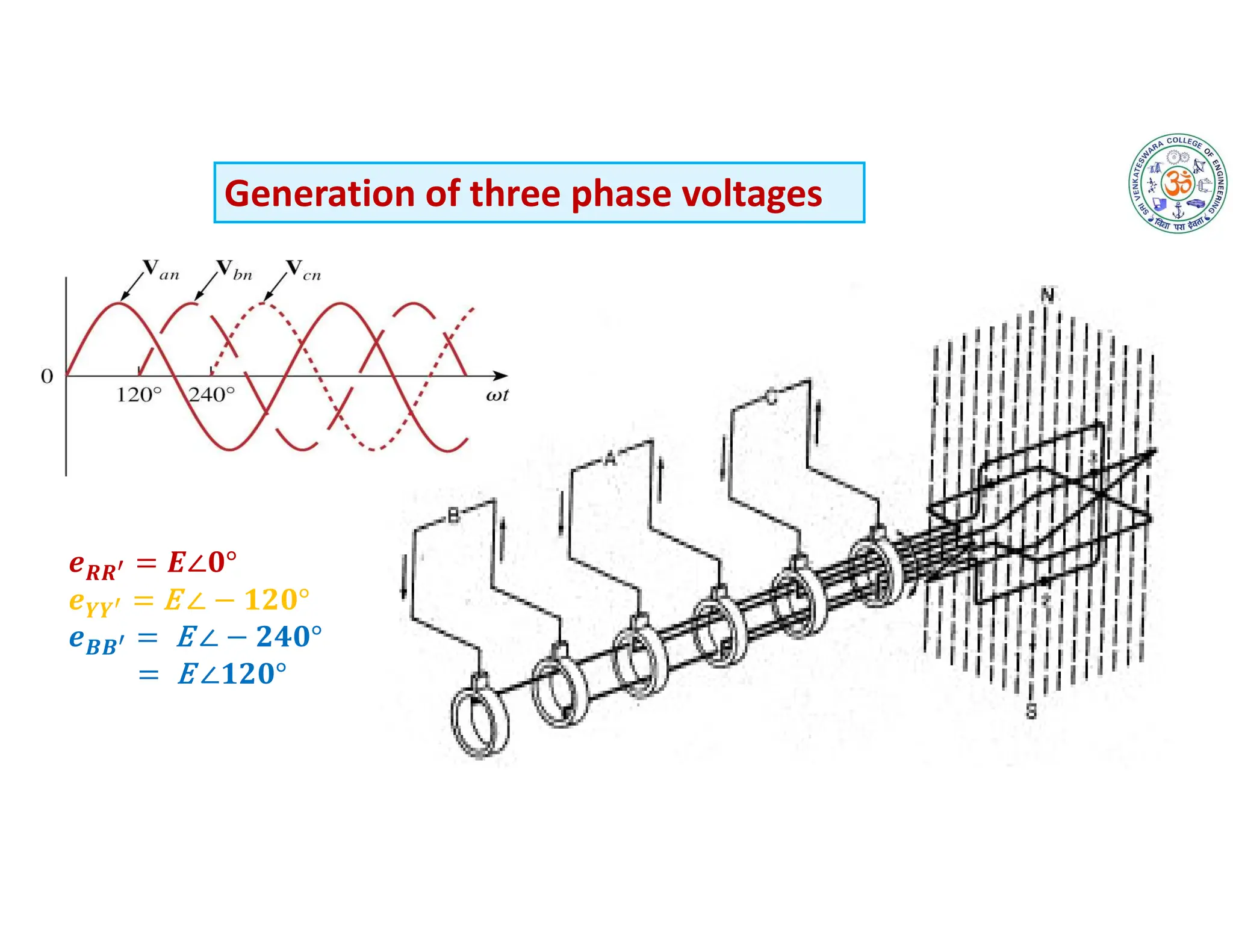
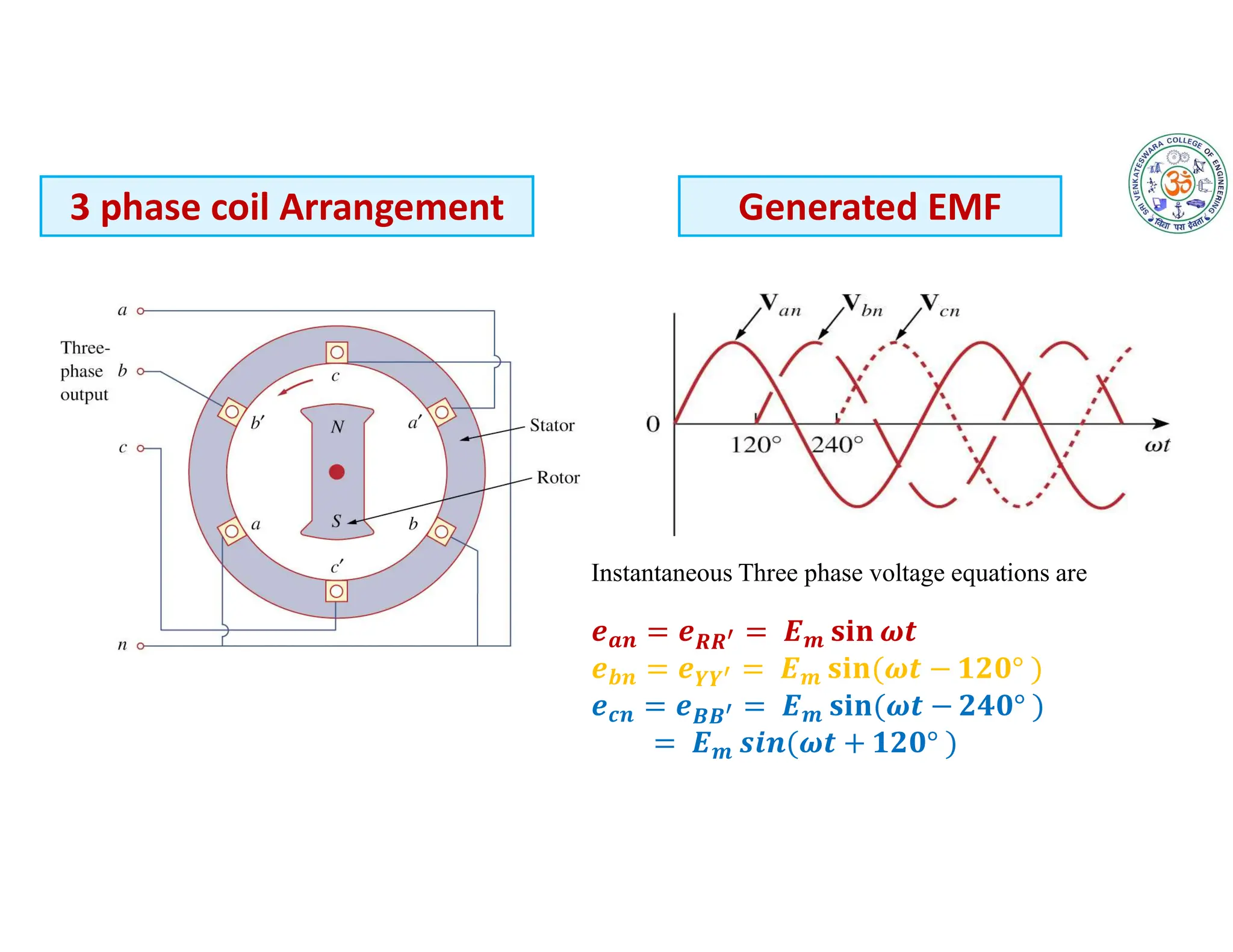
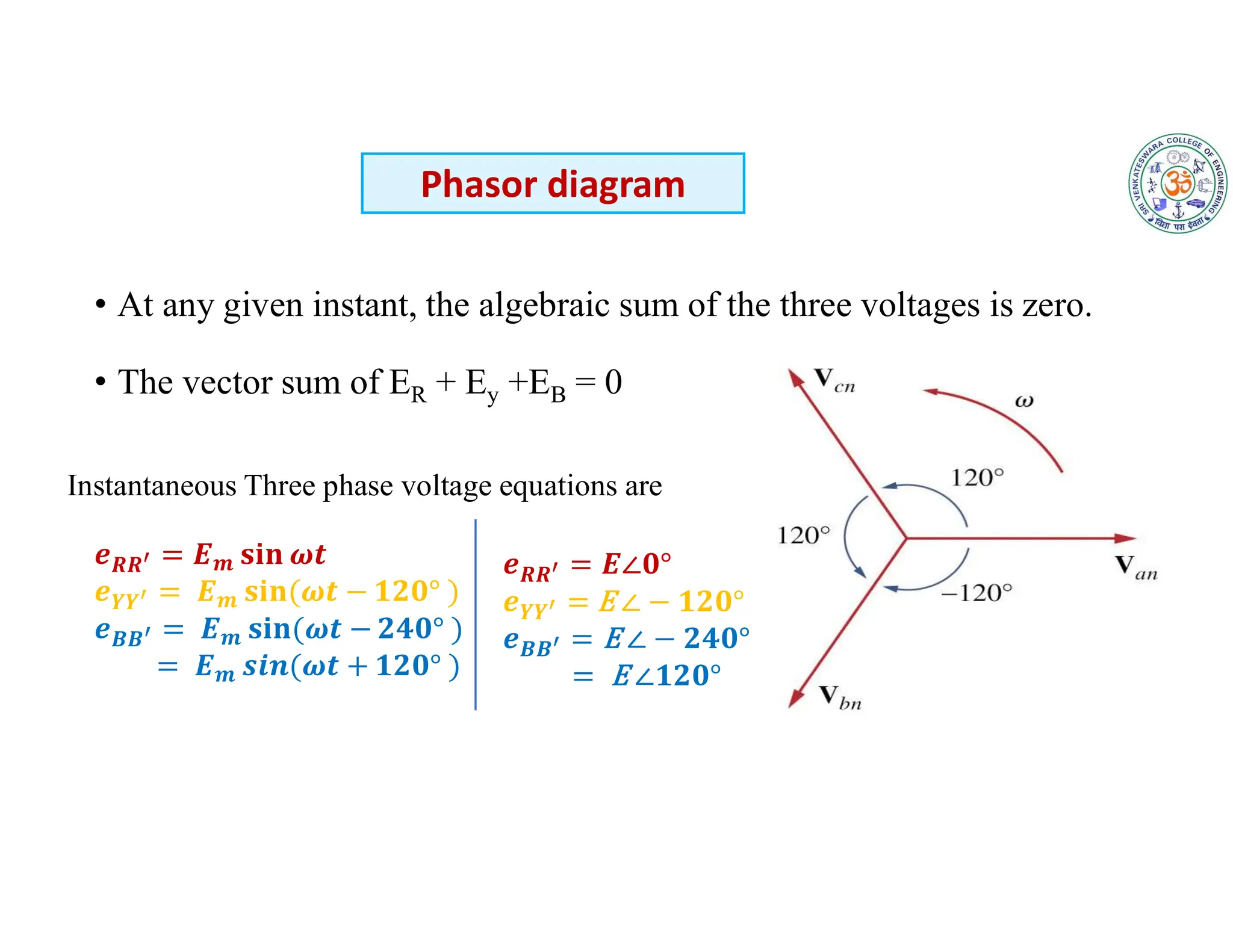
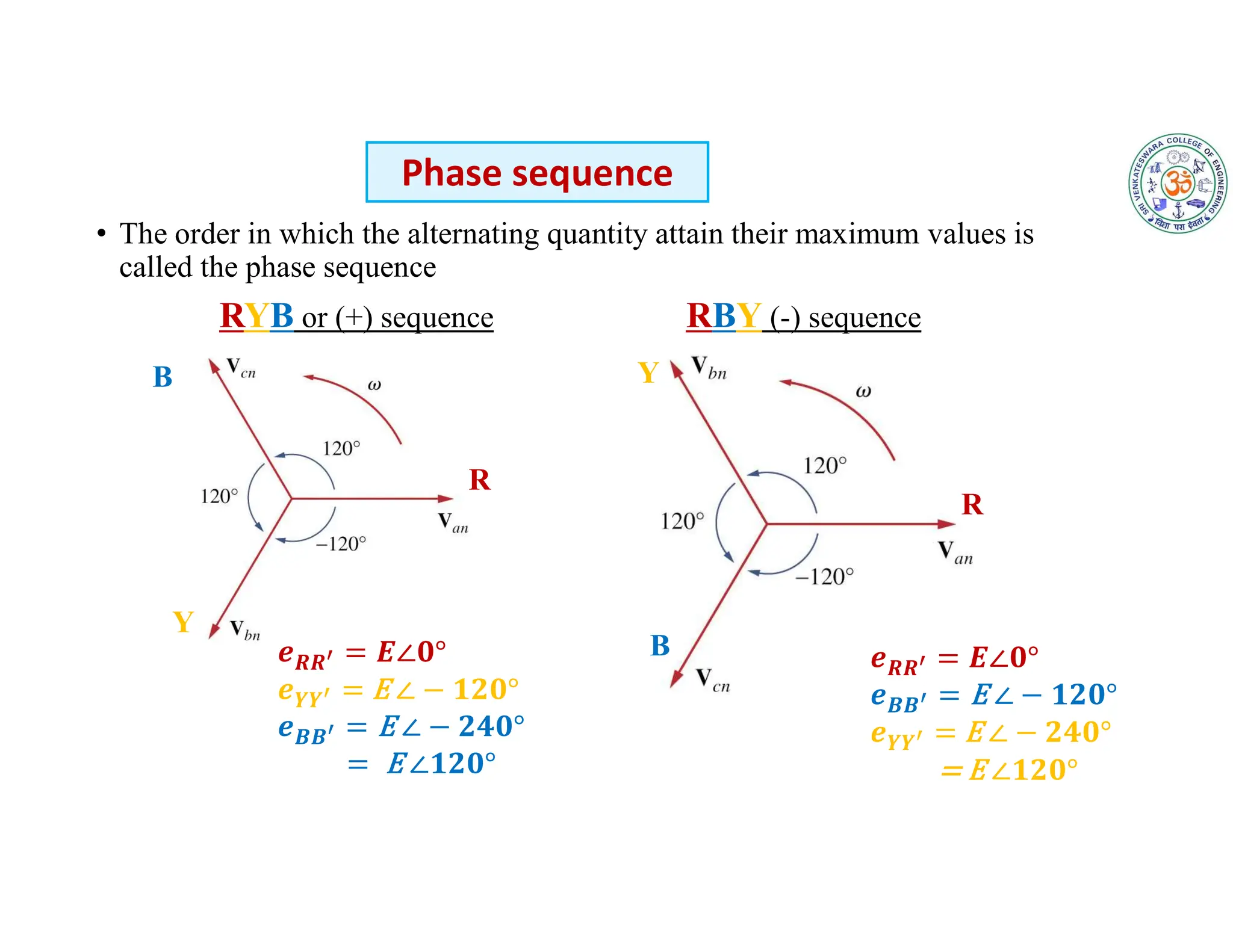
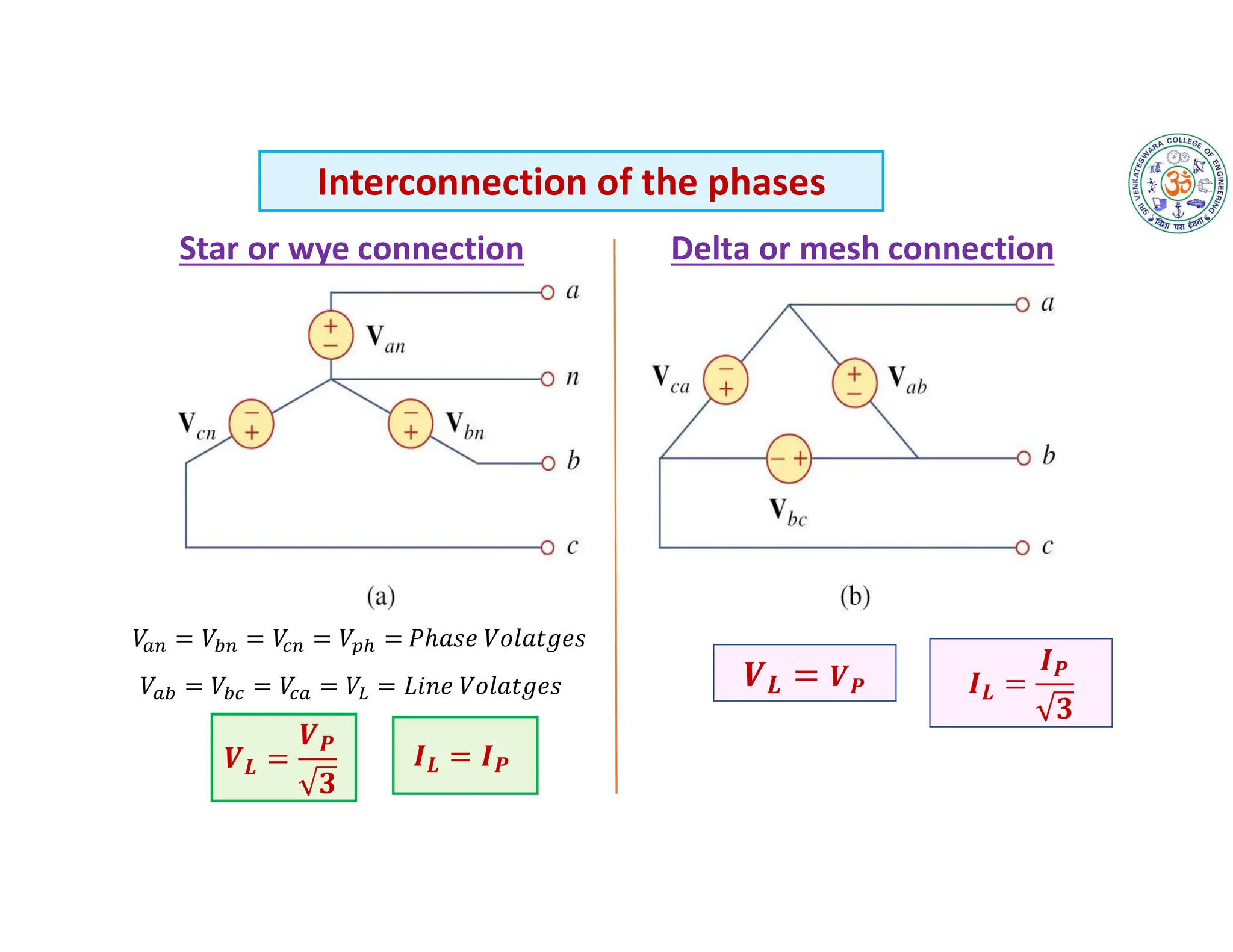
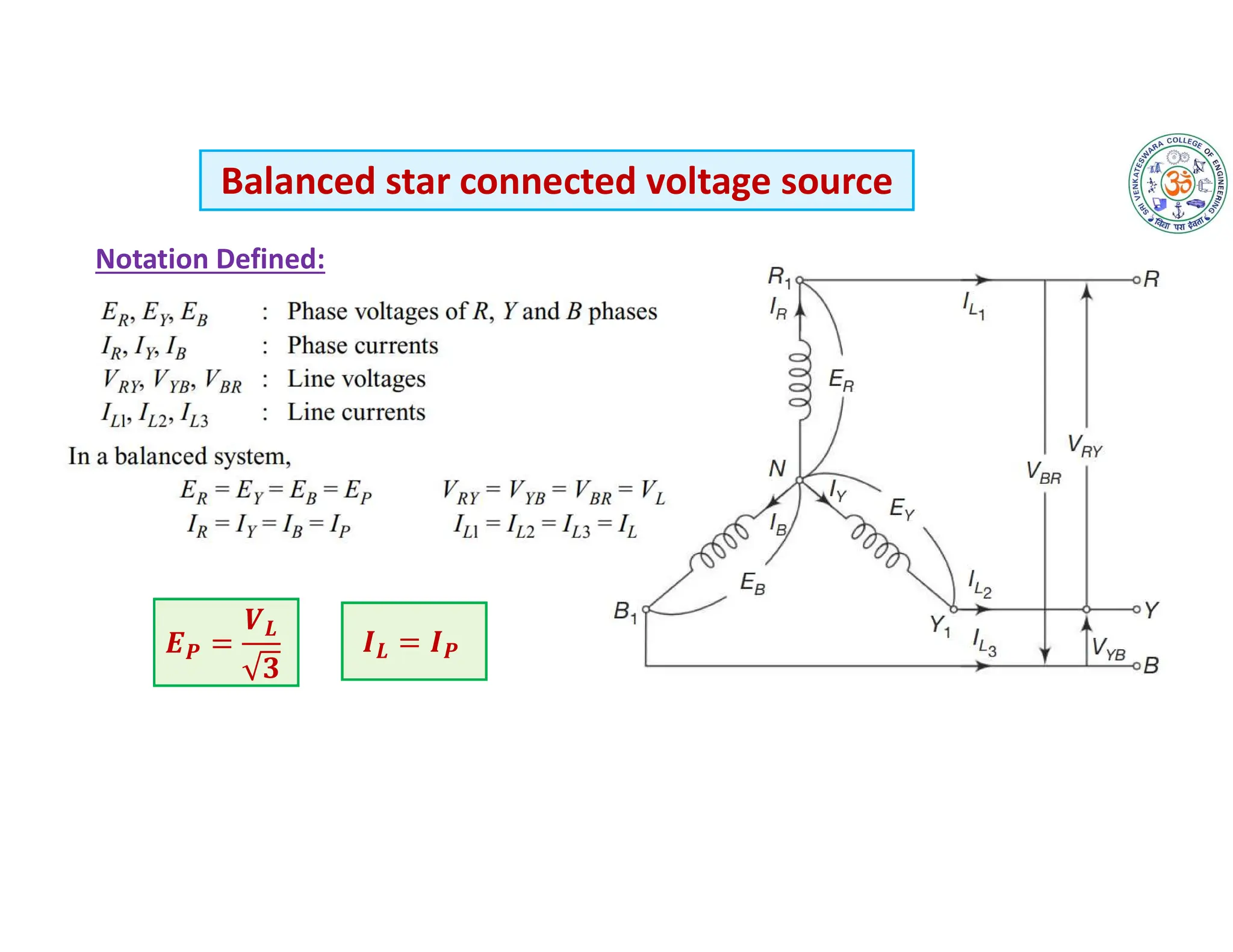
The document covers fundamental concepts related to electrical circuits, specifically focusing on AC circuit analysis. It discusses AC waveforms, parameters like frequency and amplitude, as well as various circuit components such as resistors, inductors, and capacitors in both series and parallel configurations. Additionally, it includes formulas for voltage and current in AC circuits and practical problem-solving examples.