1. (続) Rで力学系
2012/5/26
Tokyo.R #23
@xiangze750

2. Agenda
 力学系とは
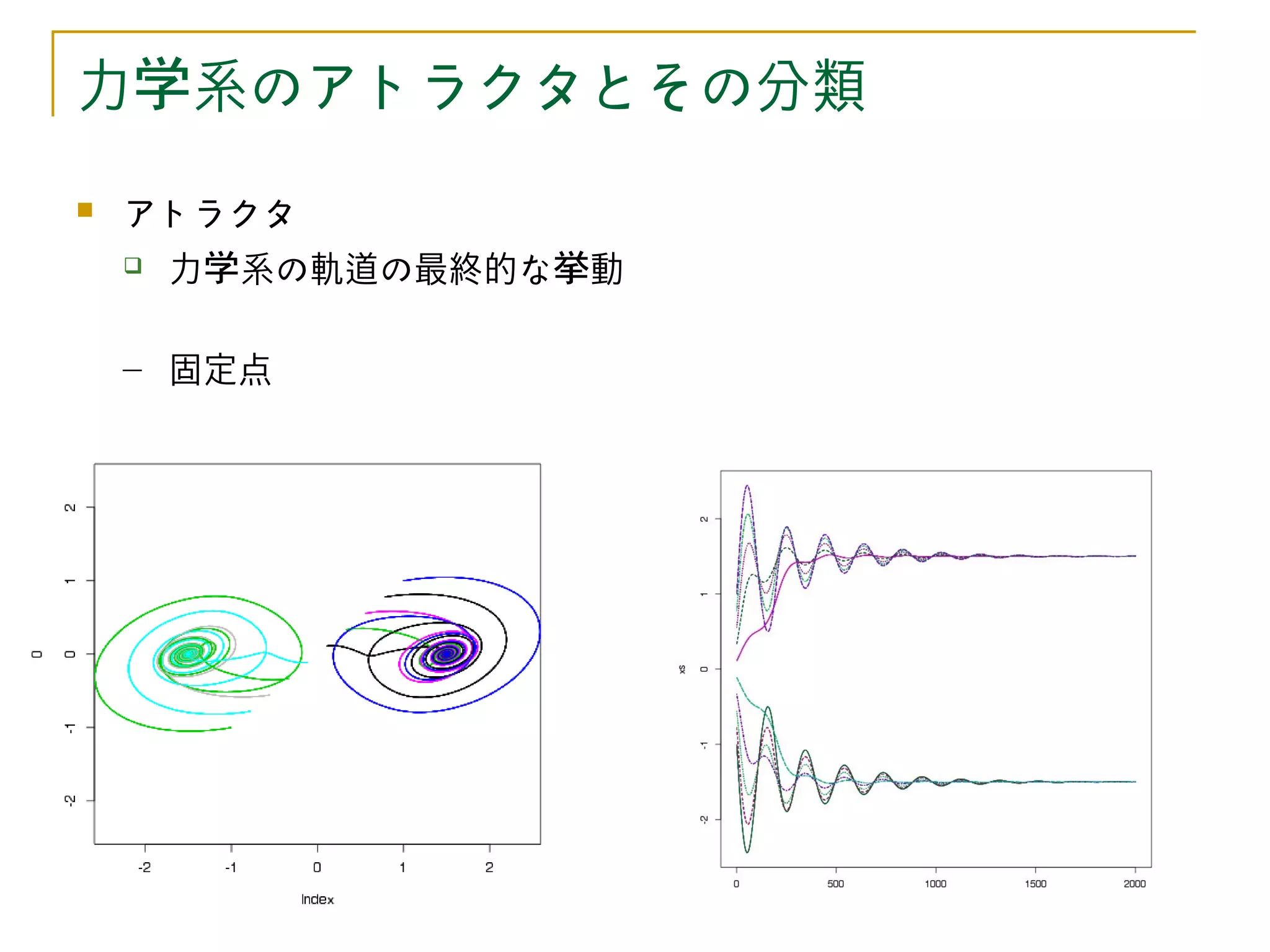
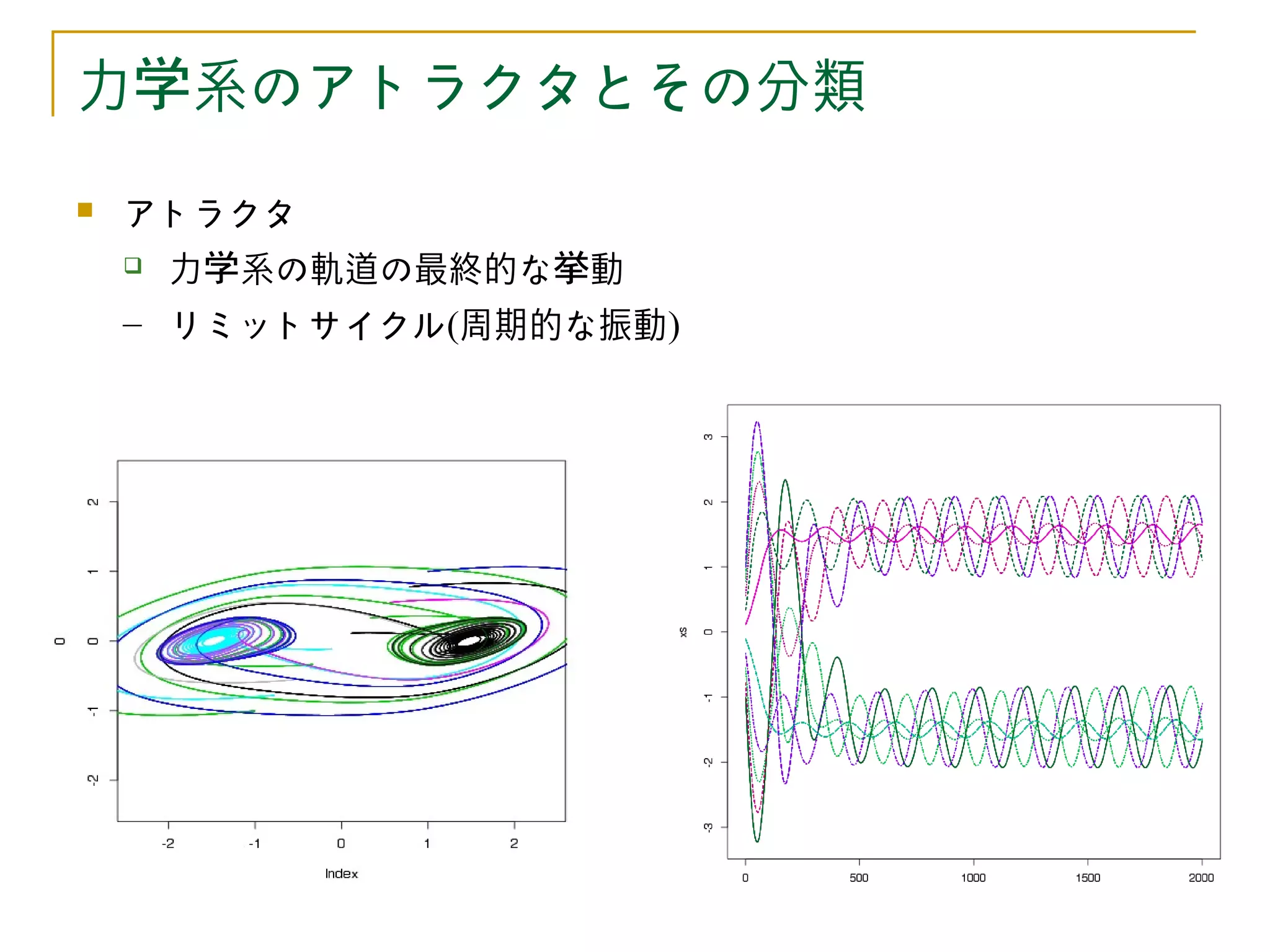
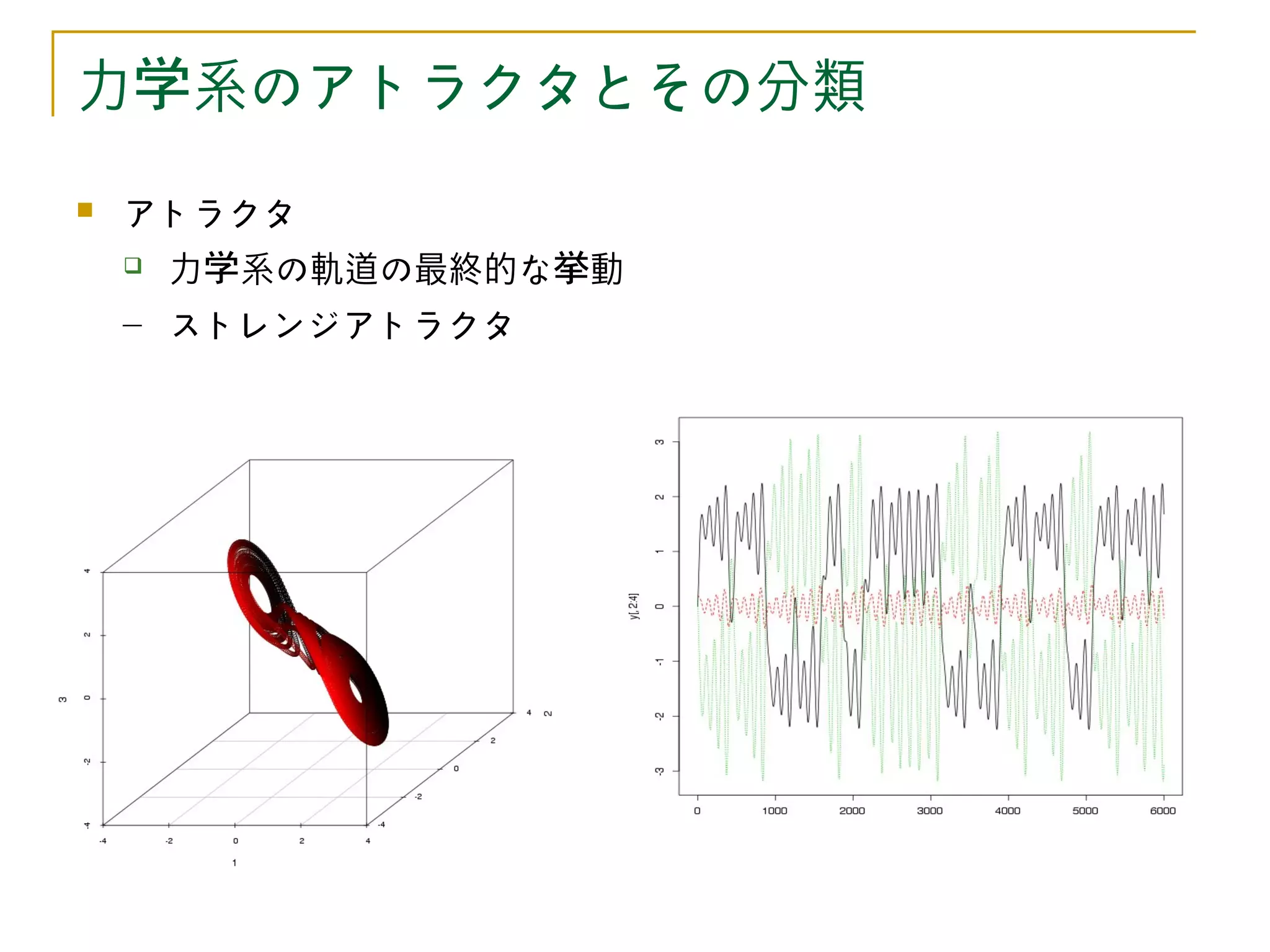
 アトラクタ
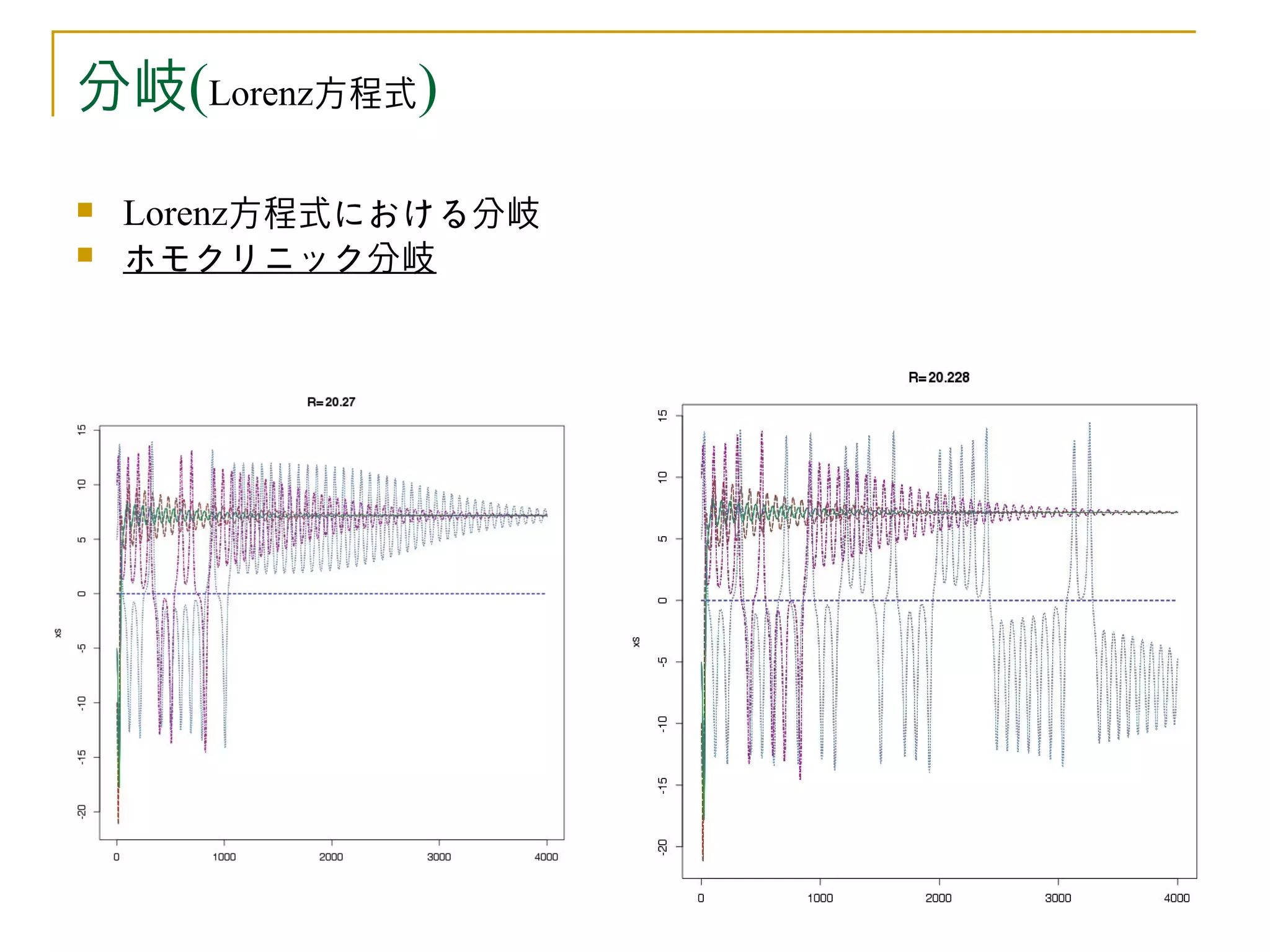
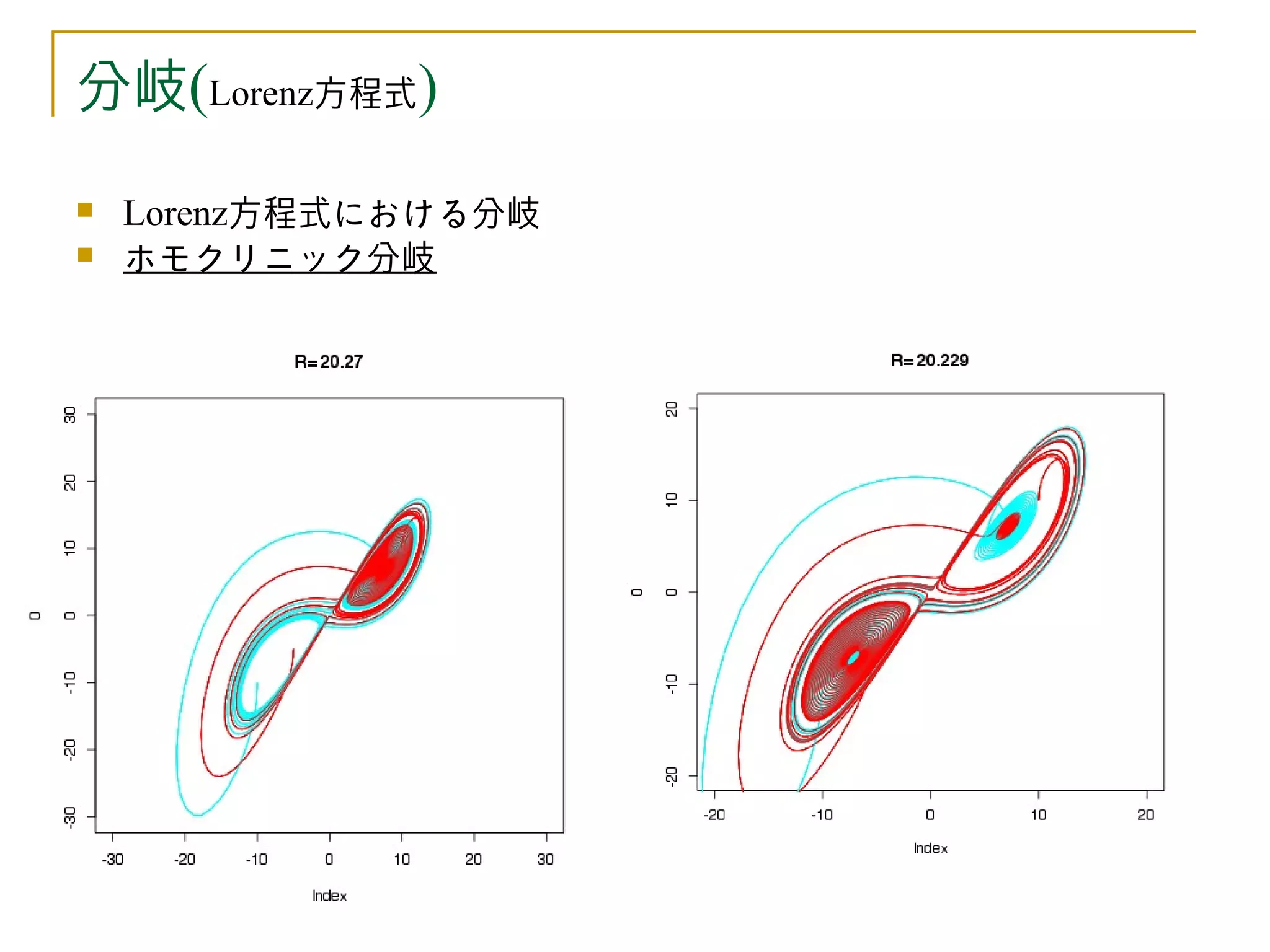
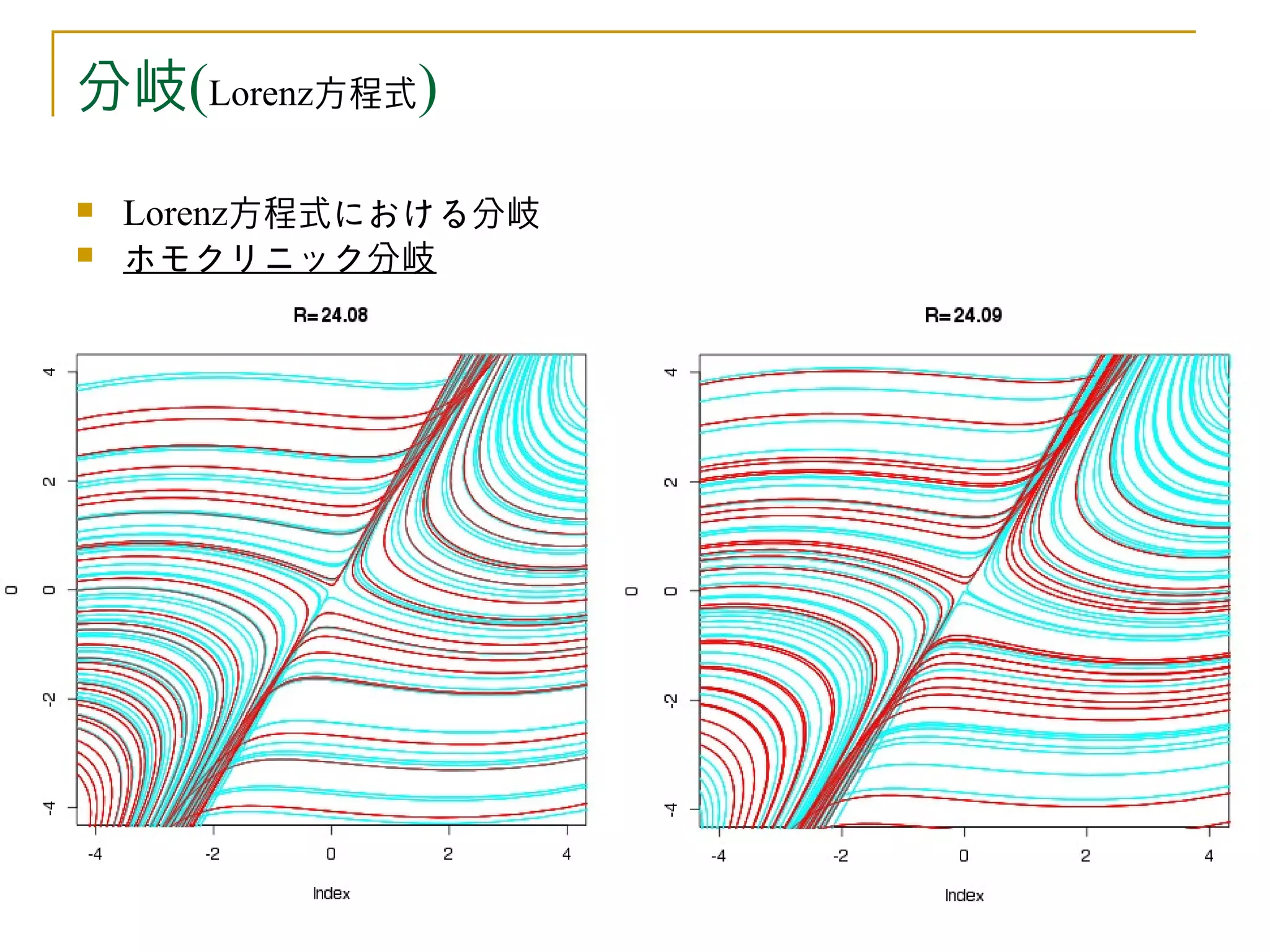
 分岐
 力学系の性質をとらえる
 見えない構造をみる

3. Agenda
 Tsukuba.Rでの発表
「Rで分かる力学系 ～分岐の様子を可視化してみる～」
http://arataka.wordpress.com/2009/03/02/tsukubar4-lt/
 今回は力学系の大域的分岐と”ホモクリニック軌道の可視化”に注目しま
す。

4. 力学系とは
 常微分方程式の解の大域的な振る舞いを研究する分野
 解が解析的に表示できない場合に全体的な性質を知ることができる
 天体力学の研究に由来する(３体問題)がいろいろなシステムで研究さ
れている。
 有名な例
 Chua 回路 電子回路
 Lorenz方程式(気象のモデル由来)
 Lotka voltera方程式(生態系)
 Standard map(外力の加わる振動子)
 少ない変数でありながらときに非常に複雑な時系列を生成する。

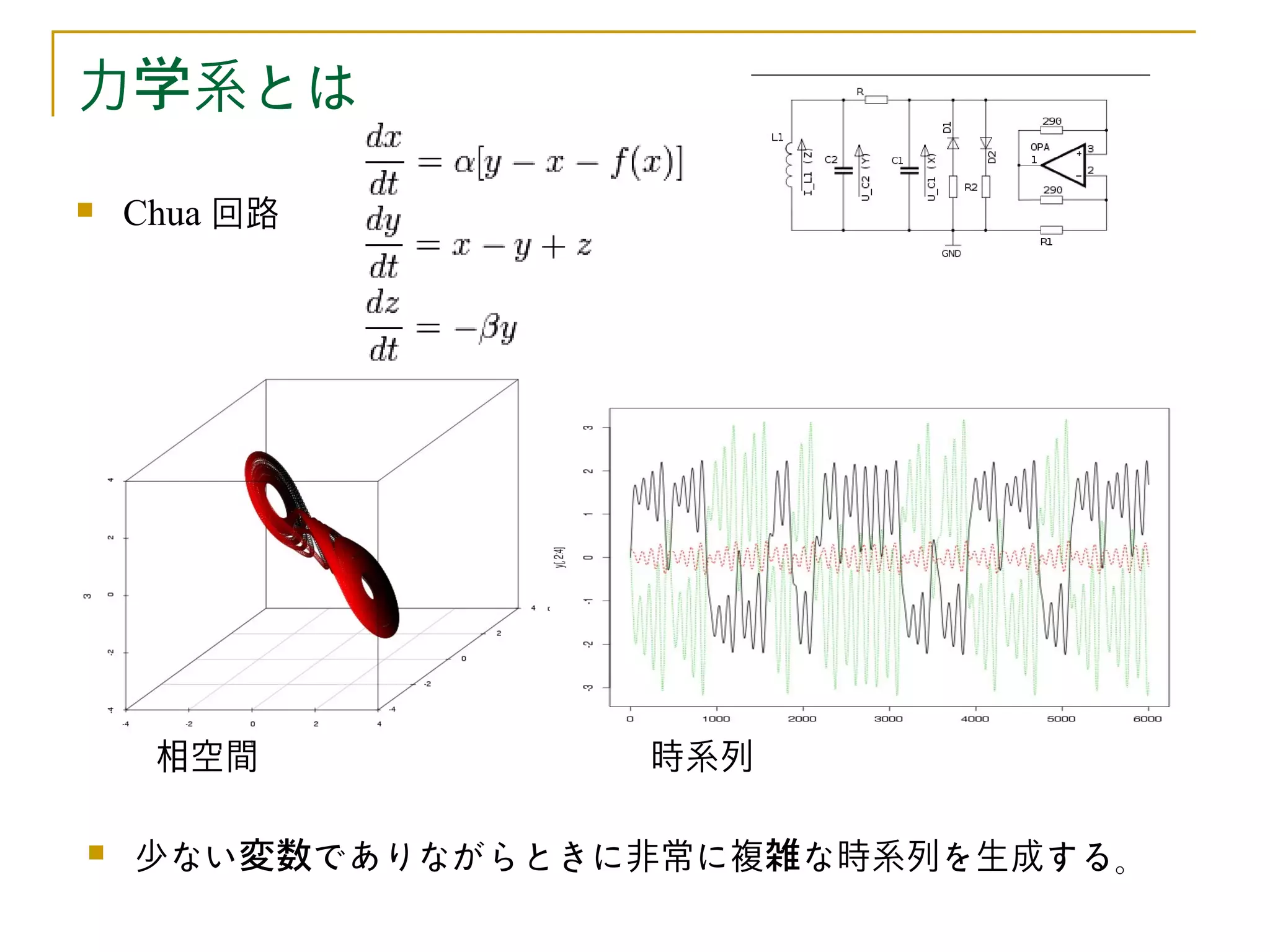
5. 力学系とは
 Chua 回路
相空間 時系列
 少ない変数でありながらときに非常に複雑な時系列を生成する。

6. 力学系のアトラクタとその分類
 アトラクタ
 力学系の軌道の最終的な挙動
– 固定点

7. 力学系のアトラクタとその分類
 アトラクタ
 力学系の軌道の最終的な挙動
– リミットサイクル(周期的な振動)

8. 力学系のアトラクタとその分類
 アトラクタ
 力学系の軌道の最終的な挙動
– ストレンジアトラクタ

9. 分岐
 １つの常微分方程式の系のパラメータを連続的に変化させるとアトラ
クタとそこへ至る解軌道の性質が大きく変化すること。
 局所的な分岐
 pitch-fork分岐(固定点が不安定になる)
Hopf分岐(固定点がリミットサイクルに変化する)
 大域的な分岐
 ホモクリニック分岐
ヘテロクリニック分岐
 カオスへ至る分岐
 周期倍分岐

10. 分岐(Lorenz方程式)
 Lorenz方程式における分岐
 ホモクリニック分岐

11. 分岐(Lorenz方程式)
 Lorenz方程式における分岐
 ホモクリニック分岐

12. 分岐(Lorenz方程式)
 Lorenz方程式における分岐
 ホモクリニック分岐

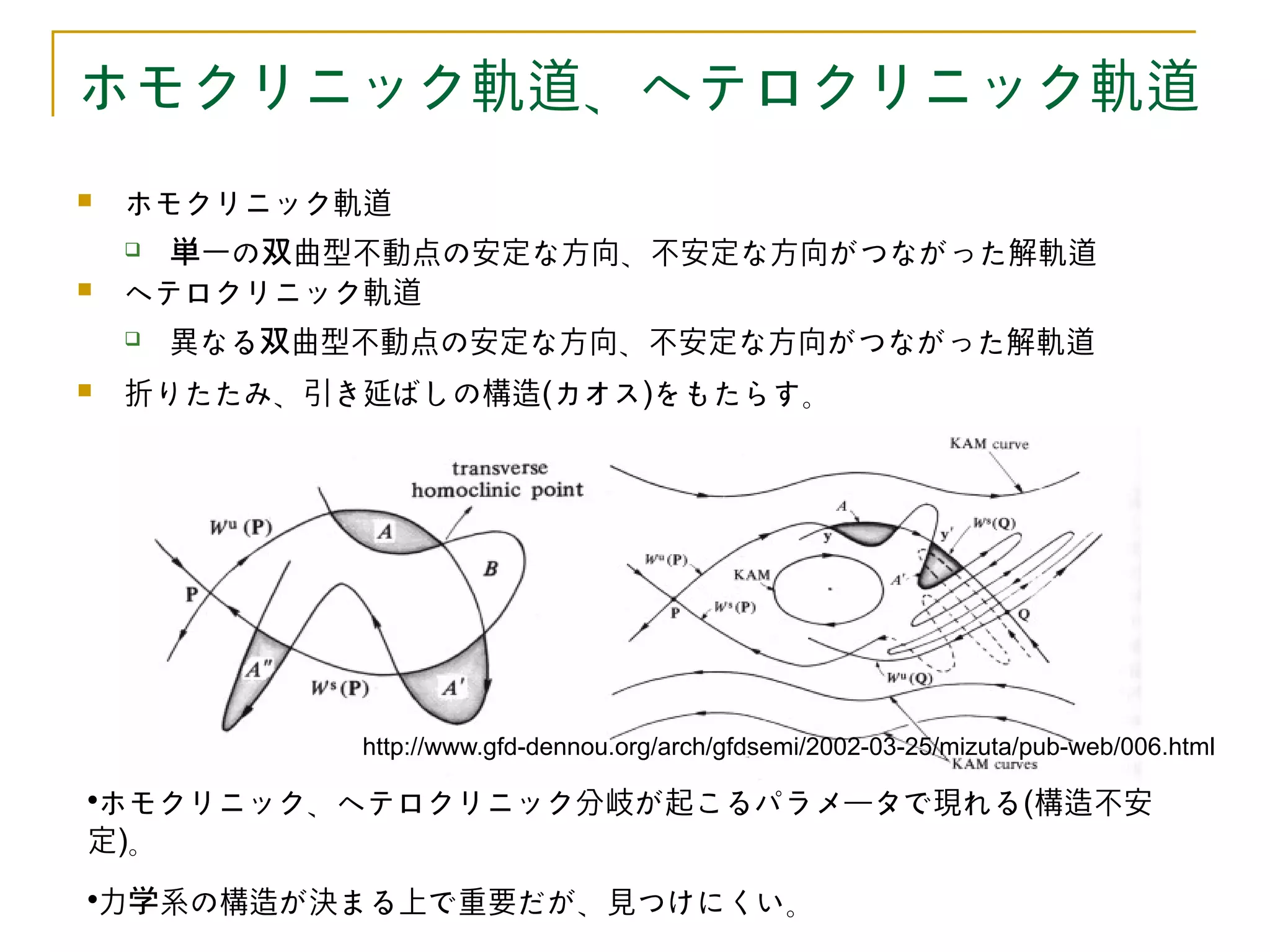
13. ホモクリニック軌道、ヘテロクリニック軌道
 ホモクリニック軌道
 単一の双曲型不動点の安定な方向、不安定な方向がつながった解軌道
 ヘテロクリニック軌道
 異なる双曲型不動点の安定な方向、不安定な方向がつながった解軌道
 折りたたみ、引き延ばしの構造(カオス)をもたらす。
http://www.gfd-dennou.org/arch/gfdsemi/2002-03-25/mizuta/pub-web/006.html
ホモクリニック、ヘテロクリニック分岐が起こるパラメータで現れる(構造不安

定)。

力学系の構造が決まる上で重要だが、見つけにくい。

14. 力学系を特徴づける量
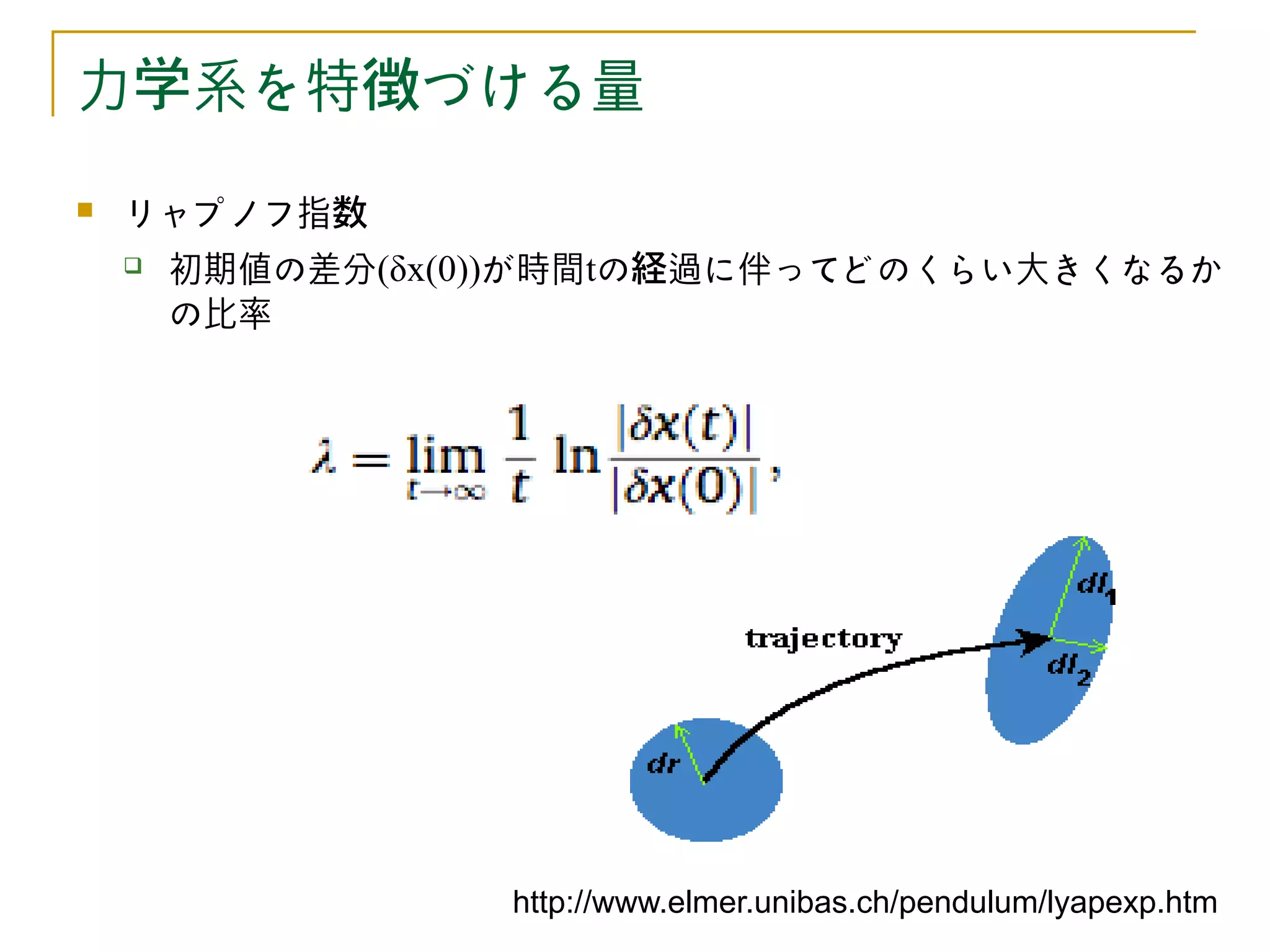
 リャプノフ指数
 初期値の差分(δx(0))が時間tの経過に伴ってどのくらい大きくなるか
の比率
http://www.elmer.unibas.ch/pendulum/lyapexp.htm

15. 見えない構造を見る
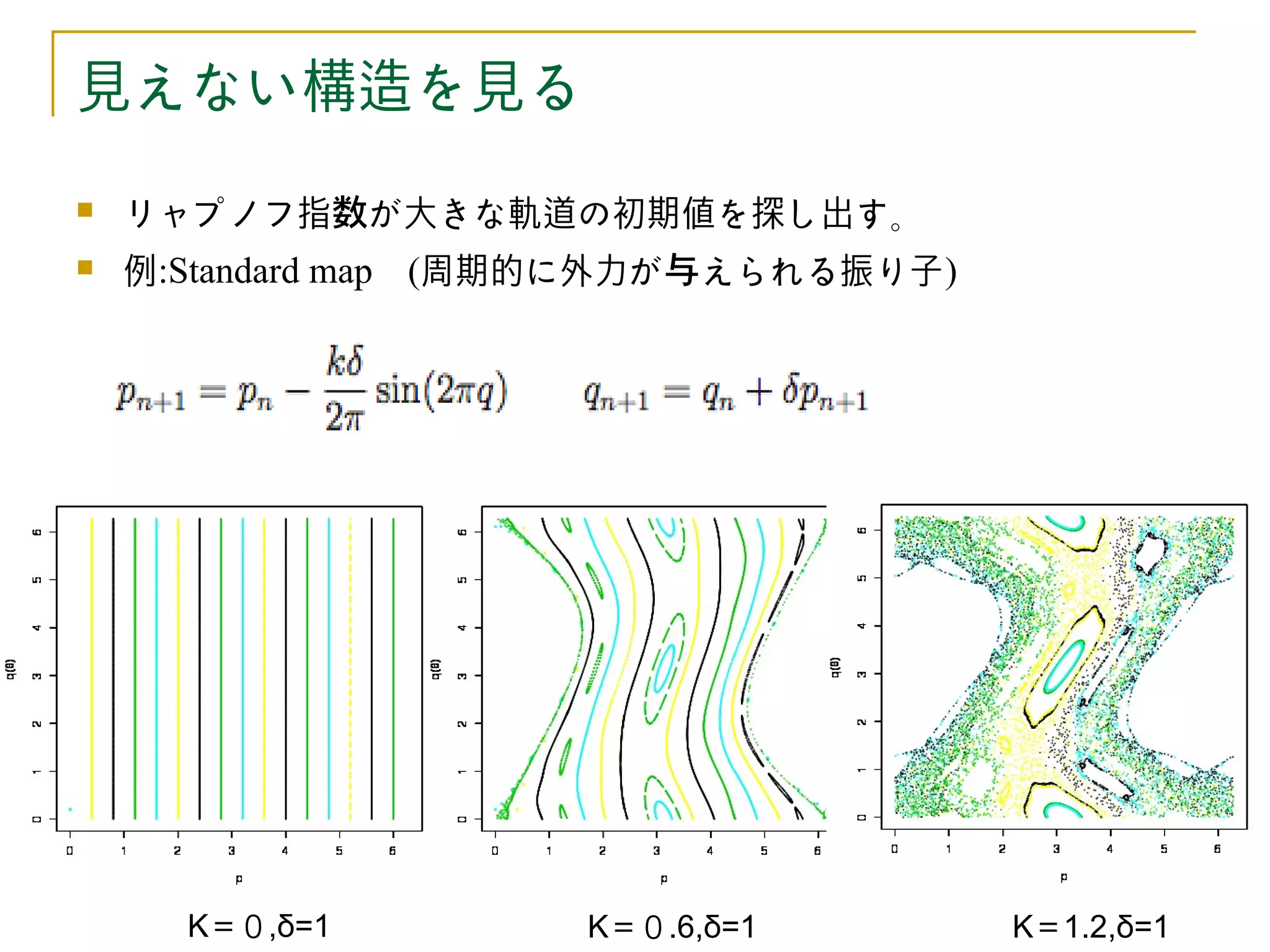
 リャプノフ指数が大きな軌道の初期値を探し出す。
 例:Standard map (周期的に外力が与えられる振り子)
K＝０,δ=1 K＝０.6,δ=1 K＝1.2,δ=1

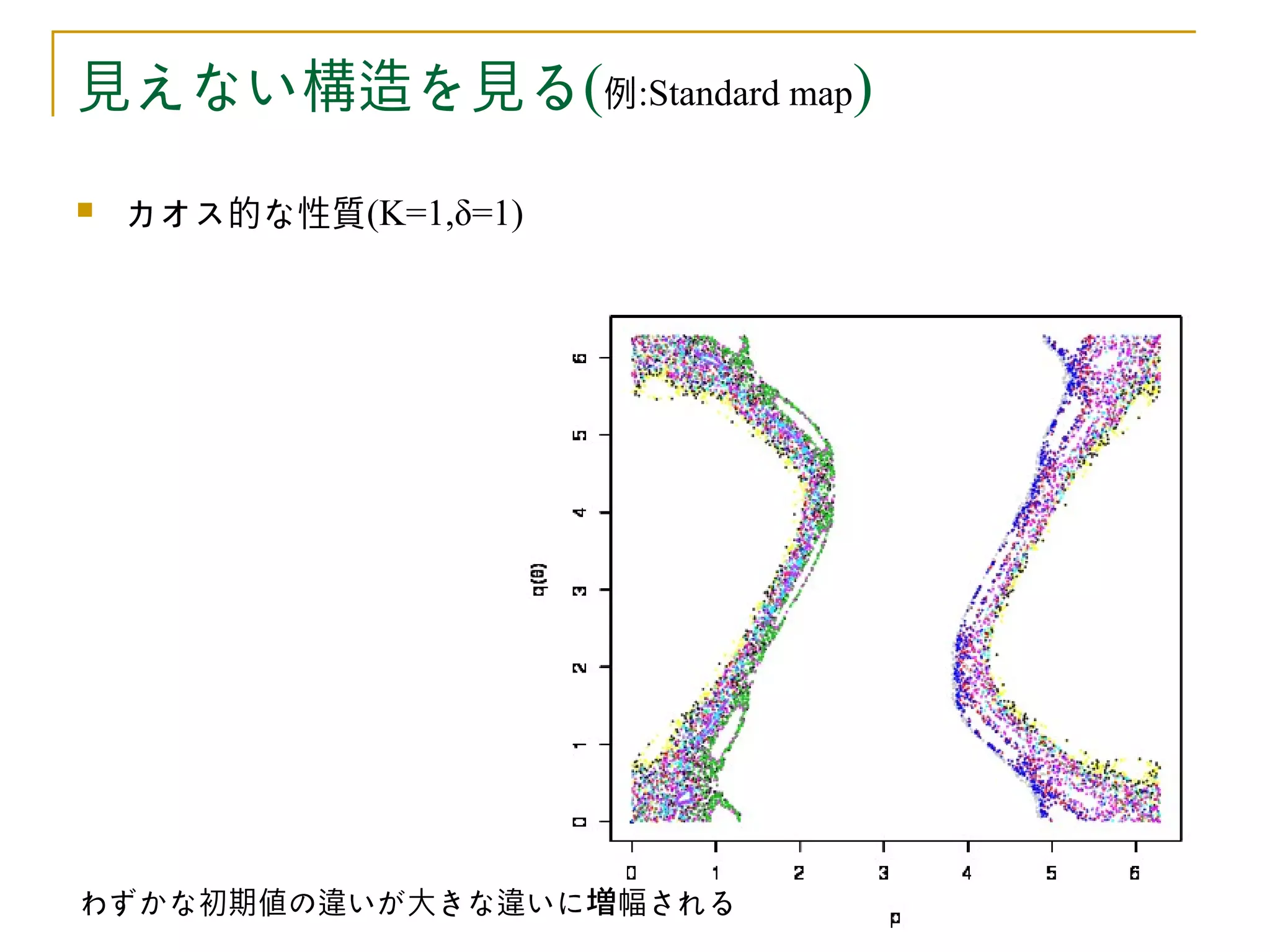
16. 見えない構造を見る
 重力相互作用するものが3つ以上ある場合軌道が複雑になる。
 ２体(天体)の相互作用を慣性運動、もう一つの天体からの影響を周期外
力とみなしたモデルがStandard mapに相当する。

17. 見えない構造を見る(例:Standard map)
 カオス的な性質(K=1,δ=1)
わずかな初期値の違いが大きな違いに増幅される

18. 手順
 初期値をN個用意する。
それぞれに対して方程式の時間発展を計算し、リャプノフ指数λNを計算
する。
 得点a*λNが大きい点の周囲に初期値を取り直す
 繰り返し

19. 結果
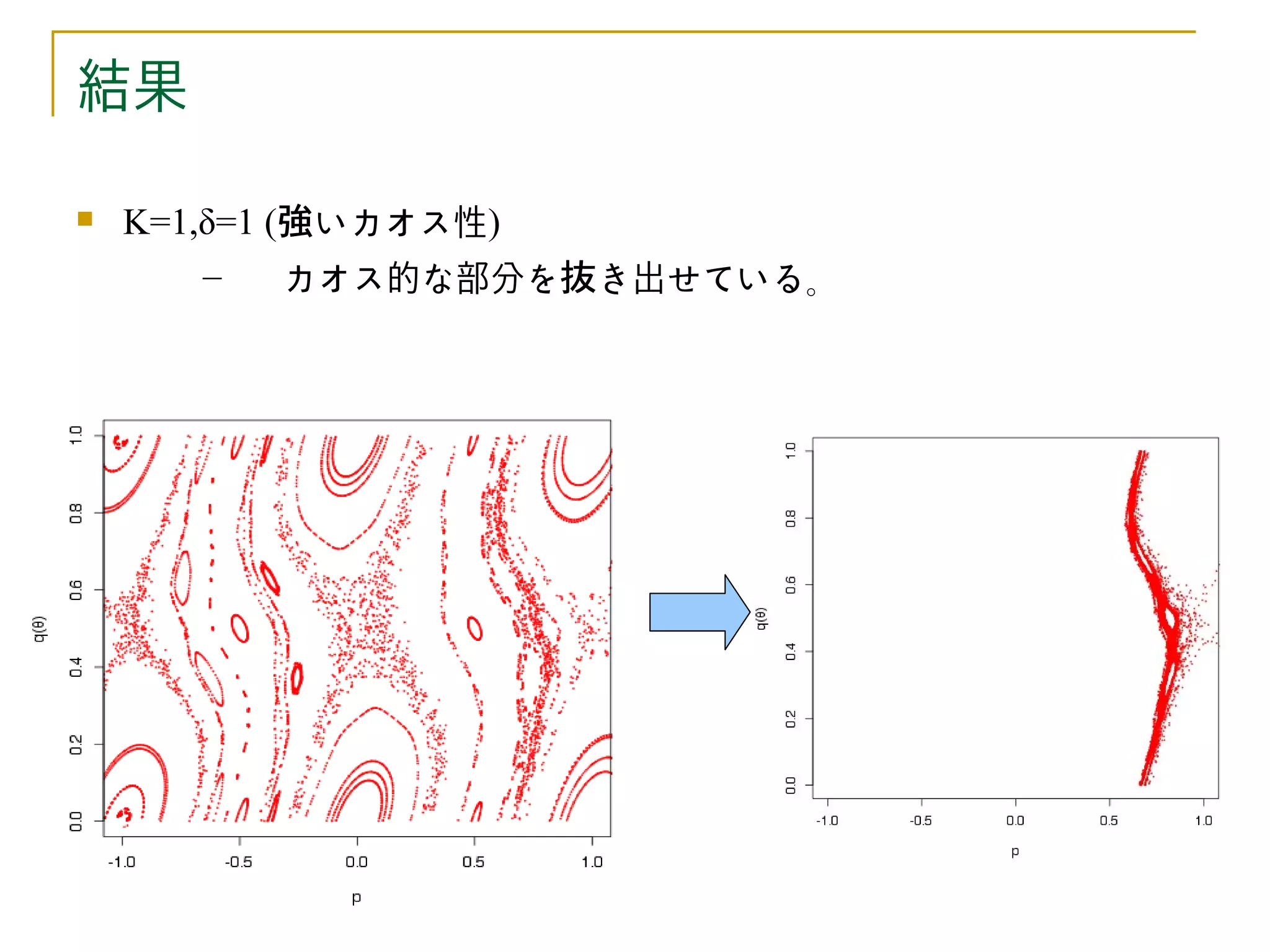
 K=1,δ=1 (強いカオス性)
– カオス的な部分を抜き出せている。

20. 結果
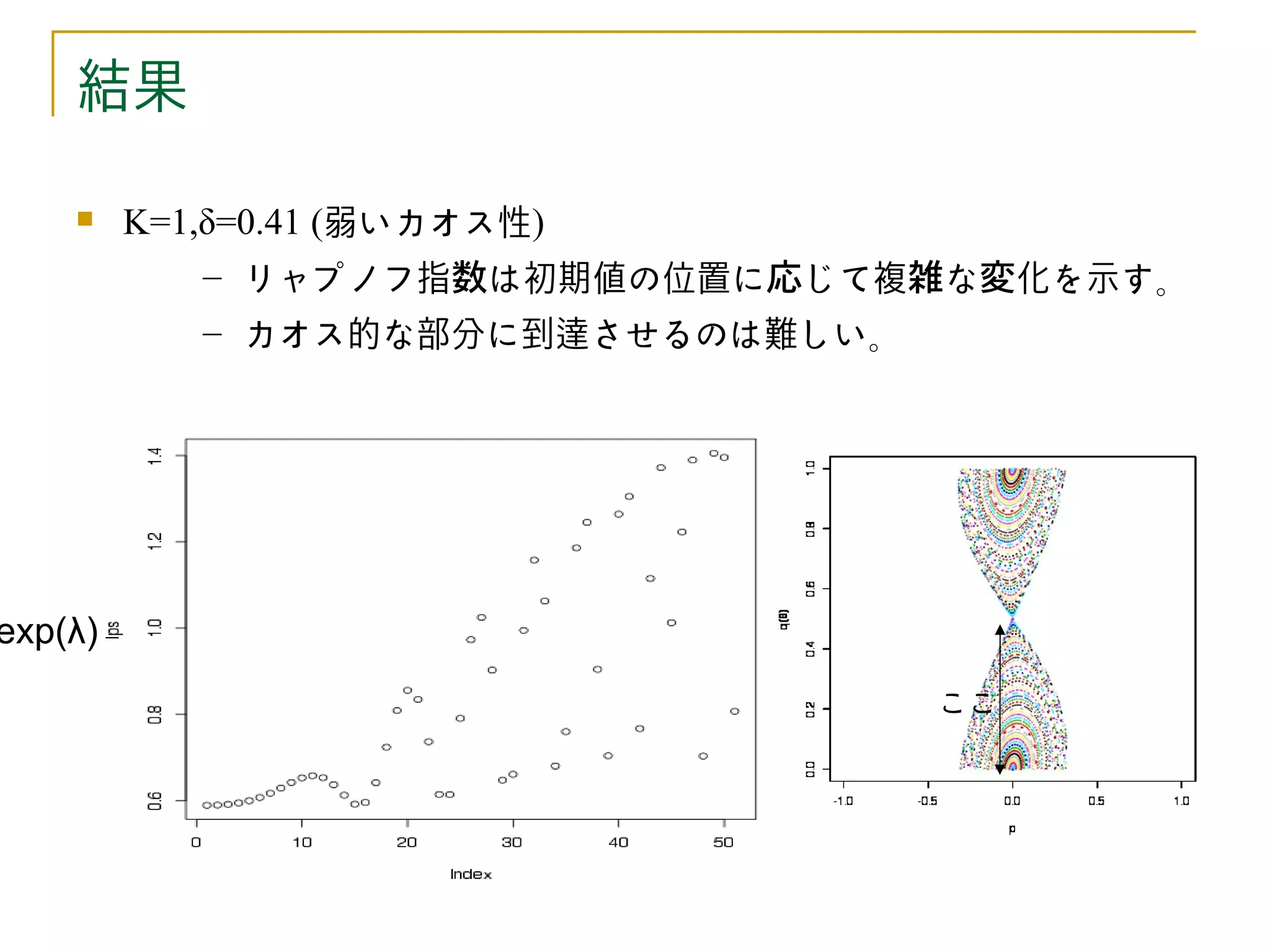
 K=1,δ=0.41 (弱いカオス性)
– リャプノフ指数は初期値の位置に応じて複雑な変化を示す。
– カオス的な部分に到達させるのは難しい。
exp(λ)
ここ

21. 結果
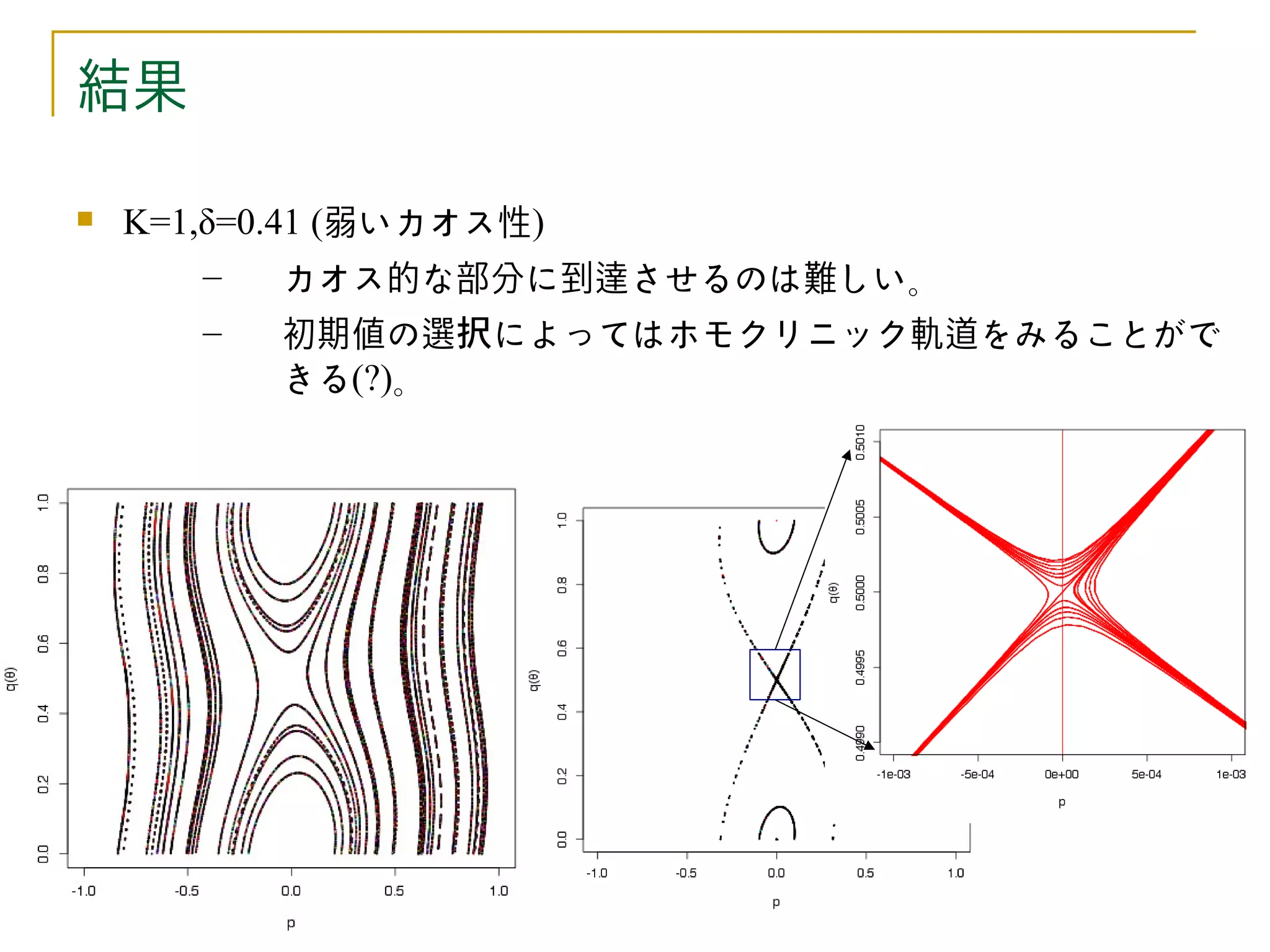
 K=1,δ=0.41 (弱いカオス性)
– カオス的な部分に到達させるのは難しい。
– 初期値の選択によってはホモクリニック軌道をみることがで
きる(?)。

22. まとめ
 少数自由度の微分方程式も時に複雑な挙動を見せる。
 力学系の性質、アトラクタの種類は分岐によって大きく変わる
 ストレンジアトラクタへ至る分岐にはホモクリニック(ヘテロクリニッ
ク)軌道の周辺で起こる。
 ホモクリニック軌道を見つけ出すことは難しいがリャプノフ指数によ
る重み付けによって可能になる。
– 多自由度の場合に威力を発揮する(はず)。

23. Reference
 Rで分かる力学系 ～分岐の様子を可視化してみる～
http://arataka.wordpress.com/2009/03/02/tsukubar4-lt/
 レプリカ交換モンテカルロ法を用いた力学系の軌道・パラメータ探索
– http://d.hatena.ne.jp/sfchaos/20110705
 これからの可視化は動画の時代～Rでanimationパッケージで動画を作
成する方法@Tokyo.R #20
– http://d.hatena.ne.jp/EulerDijkstra/20120129/1327834316
 論文
– Probing rare physical trajectories with Lyapunov weighted dynamics
– Identifying rare chaotic and regular trajectories in dynamical systems
with Lyapunov weighted path sampling
 ベクトル場のホモクリニック分岐と Lorenz-type attractor
– http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0806-09.pdf