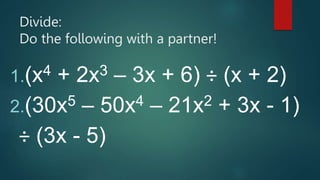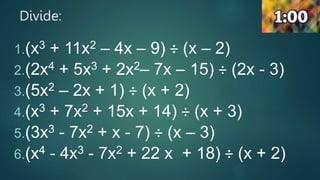The document discusses the steps to perform long division of polynomials. It explains that polynomials are divided by arranging terms in descending order and then repeatedly dividing and subtracting terms until the remainder is zero or has a lower degree than the divisor. The key steps are to divide the first term of the dividend by the first term of the divisor to get the first term of the quotient, multiply the divisor by the quotient term, and subtract it from the dividend. This process is repeated until the division is complete.

1. DIVISION OF
POLYNOMIALS
LONG DIVISION

2. COMPLETE ME IF YOU CAN!
Give the missing term/s to make each
polynomial complete.
1. x4 + x3- 3
2. 12x4 + 3
3. 24x4 + 6x3 – 3
4. 9x4 - 2x + 1
5. 21x7 - 9x3 +5

3. Quick Thinking Only!
Divide
1. x4 ÷ x3
2. 12x4 ÷ 3x2
3. 24x4 ÷ 6x3
4. 9x4 ÷ 2x
5. 21x7 ÷ 9x3

4. Divide:
Do the following with a partner!
1.(x4 + 2x3 – 3x + 6) ÷ (x + 2)
2.(30x5 – 50x4 – 21x2 + 3x - 1)
÷ (3x - 5)

5. 1. What are the steps to divide a
polynomial by another polynomial?
2. How can you determine if the answer is
correct or not?
3. Is there another way to get the correct
answer? Briefly explain your solution.

6. To divide polynomial by another
polynomial using long division…
1. Arrange the terms in both the divisor and the dividend in
descending order.
2. Divide the first term of the dividend by the first term of the divisor to
get the first term of the quotient.
3. Multiply the divisor by the first term of the quotient and subtract the
product from the dividend.
4. Using the remainder, repeat the process, thus finding the second
term of the quotient.
 Continue the process until the remainder is zero or the remainder is
of a lower degree than the divisor

7. Divide the given polynomials. Show your
complete solution. And express your answer in
the form P(x) = Q(x) D(x) + R(x)
1. (x3 + 2x2 – x - 2) ÷ (x - 1)
2. (x5 + 2x4 + 6x + 4x2 + 9x3 - 2) ÷ (x + 2)

8. DIVISION OF
POLYNOMIALS
LONG DIVISION

9. QUICK THINKING ONLY!
Divide and Write.
EXAMPLE:
19 ÷ 5 = 3 + 4/5 ⟷ 19 = 3(5) + 4

10. QUICK THINKING ONLY!
Divide and Write.
1. 29 ÷ 5 = _____ ⟷ ______
2. 34 ÷ 7 = _____ ⟷ ______
3. 145 ÷ 11 = _____ ⟷ ______
4. 122 ÷ 7 = ____ ⟷ _____
5. 219 ÷15 = ____ ⟷ _____

11. Perform the indicated operations.
1. (x3 + 11x2 – 9) + (x3 + x2 – 4x – 9)
2. (x3 + 11x2 – 4x – 9) - (x – 2)
3. (4x – 9) (x – 2)
4. (x3 ) ÷ (x )

12. 1.What are the steps to divide a
polynomial by another polynomial?
2.How can you determine if the
answer is correct or not?

13. To divide polynomial by another
polynomial using long division…
1. Arrange the terms in both the divisor and the dividend in
descending order.
2. Divide the first term of the dividend by the first term of the
divisor to get the first term of the quotient.
3. Multiply the divisor by the first term of the quotient and
subtract the product from the dividend.
4. Using the remainder, repeat the process, thus finding the
second term of the quotient.
5. Continue the process until the remainder is zero or the
remainder is of a lower degree than the divisor

14. Divide:
1.(x3 + 11x2 – 4x – 9) ÷ (x – 2)
2.(2x4 + 5x3 + 2x2– 7x – 15) ÷ (2x - 3)
3.(5x2 – 2x + 1) ÷ (x + 2)
4.(x3 + 7x2 + 15x + 14) ÷ (x + 3)
5.(3x3 - 7x2 + x - 7) ÷ (x – 3)
6.(x4 - 4x3 - 7x2 + 22 x + 18) ÷ (x + 2)

15. Determine the remainder using long division
and show the complete solution.
1. (x3 + x2 – 22x - 25) ÷ (x + 2)
2. (4x4 + 21x3 - 26x2 + 28x - 10) ÷ (x + 5)
3. (6x3 - 25x2 – 31x + 20) ÷ (3x - 2)