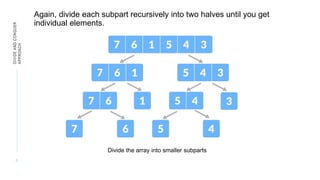
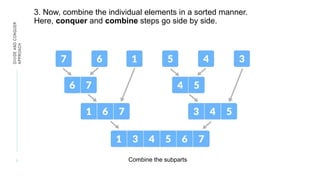
This document discusses the divide and conquer algorithmic approach. It begins with an acknowledgement and then outlines the contents to be covered, which includes an introduction to divide and conquer, the procedure involving dividing the problem into subproblems, conquering the subproblems, and combining the results. An example of applying divide and conquer to merge sort is provided. The algorithm is presented along with advantages like solving difficult problems and allowing for parallelism. Disadvantages involving recursion overhead are also discussed. The document concludes that divide and conquer is a recursive problem-solving approach that breaks problems into smaller subproblems to reduce time complexity.

1. GOVERNMENT COLLEGE OF
ENGINEERING AND TEXTILE
TECHNOLOGY, SERAMPORE
Divide And Conquer Approach With
Examples
Presented By Muktarul Hoque
Guided by By Mr. Biplab Mahapatra
State Aided College Teacher, IT Department

2. ACKNOWLEDGEMENT
DIVIDE
AND
CONQUER
APPROACH
2
I would like to express my special thanks of gratitude to Mr.
Biplab Mahapatra who gave me the golden opportunity to do
the illustration on the topic Divide And Conquer Approach, which
also helped me in doing a lot of research and I would come
to know about so many new things. Without the assistance of
our revered professors my presentation would not have
taken shape.

3. CONTENTS
DIVIDE
AND
CONQUER
APPROACH
3
Introduction: Divide and Conquer Approach
Procedure
Algorithm
Time Complexity
Advantages
Disadvantages
Conclusion
Refrences
Examples

4. INTRODUCTION
Divide and Conquer is an algorithmic pattern. In
algorithmic methods, the design is to take a dispute
on a huge input, break the input into minor pieces,
decide the problem on each of the small pieces,
and then merge the piecewise solutions into a
global solution. This mechanism of solving the
problem is called the Divide & Conquer Strategy.

5. PROCEDURE
DIVIDE
AND
CONQUER
APPROACH
5
A typical Divide and Conquer algorithm solves a problem using the following three
steps.
1.Divide: Break the given problem into subproblems of same type. This step involves
breaking the problem into smaller sub-problems. Sub-problems should represent a
part of the original problem. This step generally takes a recursive approach to divide
the problem until no sub-problem is further divisible. At this stage, sub-problems
become atomic in nature but still represent some part of the actual problem.
2.Conquer: Recursively solve these sub-problems. This step receives a lot of smaller
sub-problems to be solved. Generally, at this level, the problems are considered
'solved' on their own.
3.Combine: Appropriately combine the answers. When the smaller sub-problems are
solved, this stage recursively combines them until they formulate a solution of the
original problem. This algorithmic approach works recursively and conquer & merge
steps works so close that they appear as one.

6. EXAMPLE
DIVIDE
AND
CONQUER
APPROACH
6
• Let us understand this concept with the help of an example.
• 1.Let the given array be:
Array for merge sort

7. 7
DIVIDE
AND
CONQUER
APPROACH
2.Divide the array into two halves.
Divide the array into two subparts

8. 8
DIVIDE
AND
CONQUER
APPROACH
Again, divide each subpart recursively into two halves until you get
individual elements.
Divide the array into smaller subparts

9. 3. Now, combine the individual elements in a sorted manner.
Here, conquer and combine steps go side by side.
9
DIVIDE
AND
CONQUER
APPROACH
Combine the subparts

10. ALGORITHM
DIVIDE
AND
CONQUER
APPROACH
1 0
DAC(P){
{
if(small(p))
{
S(p)
}
else
{
divide P into P1 P2 P3 .....Pk
Apply DAC(P1),DAC(P2),DAC(P3)......DAC(PK)
Combine(DAC(P1),DAC(P2),DAC(P3)....DAC(PK)
}
}

11. ADVANTAGE
DIVIDE
AND
CONQUER
APPROACH
1 1
Solving difficult problems: It is a powerful method for solving
difficult problems. Dividing the problem into subproblems so that
subproblems can be combined again is a major difficulty in
designing a new algorithm. For many such problem this algorithm
provides a simple solution.
Parallelism: Since it allows us to solve the subprblems
independently, this allows for execution in multi-processor
machines, especially shared-memory systems where the
communication of data between processors does not need to be
planned in advance, because different subproblems can be
executed on different processors.
Memory access: It naturally tend to make efficient use of memory
caches. This is because once a subproblem is small, all its
subproblems can be solved within the cache, without accessing
the slower main memory.

12. DISADVANTAGES
DIVIDE
AND
CONQUER
APPROACH
1 2
One disadvantage of this approach is that recursion is slow. This is beacause
of the overhead of the repeated subproblem calls. Also the algorithm need
stack for storing the calls. Actually this depends upon the implementation
style. With large enough recursive base cases , the overhead of recursion can
become negligible for many problems.

13. CONCLUSION
PRESENTATION
TITLE
1 3
Divide and Conquer is a recursive problem-
solving approach which break a problem into
smaller subproblems, recursively solve the
subproblems, and finally combines the
solutions to the subproblems to solve the
original problem. This method usually allows
us to reduce the time complexity to a large
extent.

14. 1 4
DIVIDE
AND
CONQUER
APPROACH
https://medium.com/codex/divide-and-conquer-algorithm-f766640ef038
https://www.freecodecamp.org/news/divide-and-conquer-algorithms/
https://www.javatpoint.com/divide-and-conquer-introduction
REFRENCE
S

15. THANK YOU