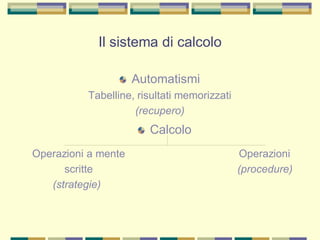
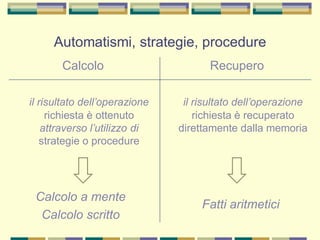
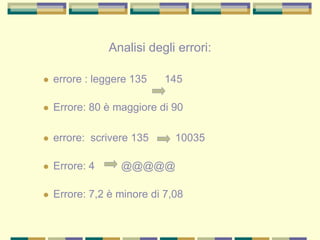
Il documento tratta delle difficoltà di calcolo e della discalculia evolutiva che affliggono molti studenti, evidenziando come queste difficoltà possano presentarsi insieme ad altri disturbi, come la dislessia. Viene discusso l'importanza di un intervento riabilitativo per migliorare le abilità numeriche, senza poter garantire una normalizzazione completa, e vengono presentati anche profili specifici di discalculia. Infine, il documento sottolinea la necessità di strategie didattiche che tengano conto delle capacità innate dei bambini nella comprensione delle quantità e dei numeri.

1. DIFFICOLTA’ DI CALCOLO E
DISCALCULIA EVOLUTIVA
Osservatorio Locale Bagheria

2. Molti studenti incontrano difficoltà
nell’apprendimento della matematica.
Due spiegazioni:
1. Difficoltà di calcolo
2. Disturbo specifico del calcolo (discalculia
evolutiva)

3. Disturbo di Calcolo Difficoltà di Calcolo
basi neurologiche
comorbilità specificità
- dislessia
- difficoltà nella
soluzione di
problemi
l’intervento riabilitativo non normalizza
ma migliora
appare in condizioni di
adeguate abilità generali e
di adeguato apprendimento
in altri ambiti
il profilo appare simile al disturbo
l’intervento riabilitativo
ottiene buoni risultati
in breve tempo

4. Disturbo delle abilità numeriche e aritmetiche
che si manifesta in bambini di intelligenza normale,
che non hanno subito danni neurologici.
Essa può presentarsi associata a dislessia,
ma è possibile che ne sia dissociata
(C. Temple; 1992)
Età della diagnosi:
fine della classe terza della scuola primaria
La discalculia evolutiva

5. I sintomi
Secondo quanto riportato nell’ ICD 10 e in accordo con quanto
Descritto nel DSM-IV i sintomi delle difficoltà aritmetiche sono:
 incapacità di comprendere i concetti di base di particolari operazioni;
 mancanza di comprensione di termini o di segni aritmetici;
 mancato riconoscimento dei simboli numerici;
 difficoltà ad attuare le manipolazioni aritmetiche standard;
 difficoltà nel comprendere quali numeri sono pertinenti al problema
aritmetico che si sta considerando;
 difficoltà ad allineare correttamente i numeri o ad inserire decimali o
simboli durante i calcoli;
 scorretta organizzazione spaziale dei calcoli;
 incapacità ad apprendere in modo soddisfacente le tabelline della mol-
plicazione.

6. DOMANDE CRUCIALI
Cosa ci garantisce un buon livello di
competenza
nelle abilità di Calcolo?
Intelligenza
numerica?
Abilità specifiche?

Quali ed in Quale
Rapporto?

7. Intelligenza Numerica?
=
Intelligere attraverso la quantità
oggi la ricerca dimostra che
E’INNATA potenziamento sviluppo
prossimale tramite
istruzione dei
processi dominio specifici
+

8. L’intelligenza numerica è innata
non solo nella nostra specie
 sta alla base di molteplici fenomeni di diversa
complessità (es: plurale, singolare)
 neonati e bambini di pochi mesi risultano già in grado
di percepire la numerosità di un insieme visivo di oggetti
senza saper contare (distinzione di quantità: 1 diverso da
tanti)
 sulla base di questa capacità innata pare che i bambini
si costruiscano delle aspettative aritmetiche basate sul
concetto di numerosità

9. Marco (5 anni): “Scritte, un po’diverse, non sono
lunghe lunghe come le parole.”
Lucia (5 anni): “Sono che ti servono quando hai i
soldini, o le bambole. Se ne hai di più o di
meno delle tue amichette.”
Luca (5 anni): “Sono numeri scritti o detti a voce. O
anche sulle dita uno per uno. Ci si conta.”
Maria (5 anni): “I numeri sono fatti per dire uno, due,
tre, e poi non sbagliare fino a dieci, e anche fino a di più.”
Cosa sono i numeri?

10. Profili di discalculia evolutiva
(Discalculia semantica)
Debolezza nella strutturazione
cognitiva delle componenti di
cognizione numerica:
Subitizing
Meccanismi di
quantificazione, seriazione,
comparazione
Strategie di calcolo a mente
(Discalculia in comorbilità)
Compromissioni a livello
procedurale e di calcolo:
Lettura e scrittura dei numeri
Incolonnamento e algoritmi
del calcolo scritto
Recupero dei fatti aritmetici
(Consensus Conference, 2007)

11. Profili di discalculia evolutiva
Dislessia per le cifre
 Compromissione dei meccanismi lessicali
Produzione di errori lessicali in compiti di lettura di numeri
arabici e scrittura sotto dettatura
Discalculia procedurale
 Difficoltà nell’acquisizione delle procedure di
calcolo senza errori di processazione numerica
Errori di riporto, prestito, incolonnamento
Discalculia per i fatti aritmetici
 Difficoltà nell’acquisizione dei fatti aritmetici
Errori nelle tabelline e nei calcoli semplici

12. ACMT (prova di primo livello)
(dalla prima alla quinta classe della scuola primaria e dalla prima
alla terza classe della scuola secondaria di 1° grado)
Abilità numeriche
 Giudizio di numerosità
 Trasformazione in cifre
 Seriazioni numeriche
 Dettato di numeri
 Enumerazione
• Abilità di calcolo
– Calcolo scritto
– Calcolo a mente
– Fatti aritmetici
Strumenti di valutazione

13. Sistema dei numeri
compiti sottesi alla capacità di
capire le quantità e le loro
trasformazioni:
Comprensione del numero
Lessico numerico
Sintassi del numero
Sistema del calcolo
compiti sottesi alla capacità di
operare sui numeri attraverso
operazioni aritmetiche:
Automatismi di calcolo
Strategie di calcolo
Procedure di calcolo
Abilità numeriche e abilità di calcolo

14. L’interrogativo cruciale a cui dobbiamo
cercare di dare una risposta è il seguente:
Come giungono i bambini a riconoscere
le quantità, a rappresentarle e a
manipolarle attraverso il complesso
sistema simbolico dei numeri?

15. Il sistema numerico
Comprensione
Comparazione, seriazioni, stima
(operazioni numeriche a base semantica)
Produzione
Lettura dei numeri Scrittura dei
numeri
(lessico numerico) (sintassi del numero)

16. Codificare semanticamente un numero equivale a
rappresentare mentalmente la quantità che esso
rappresenta e quindi a identificarne la posizione che
esso assume all’interno della linea dei numeri.
Si tratta di una rappresentazione concettuale che
corrisponde al “significato” di un numero
Comprensione del numero (semantica)

17. Comprensione del numero (semantica)
I bambini possiedono fin dalla nascita una
conoscenza astratta della matematica.
Il cervello umano possiede un meccanismo di
comprensione delle quantità numeriche, ereditato dal
mondo animale, che lo guida nell’apprendimento
della matematica. Per poter influenzare l’acquisizione
dei nomi dei numeri, questo modulo protonumerico
deve esistere già prima del periodo di crescita del
linguaggio, che si manifesta verso l’anno e mezzo di
età.

18. Comprensione del numero (semantica)
I bambini non solo nascono con la capacità di
riconoscere numerosità distinte fino a un massimo di
circa quattro, ma distinguono i cambiamenti di
numerosità provocati dall’aggiunta/sottrazione di
oggetti, ossia possiedono “aspettative aritmetiche”.

19. Comprensione del numero (semantica)
La numerosità è il numero che si ottiene quando si
contano gli elementi di un insieme
Contare significa:
 stabilire una corrispondenza biunivoca fra ciascun oggetto
dell’insieme e un numero
 stabilire una corrispondenza biunivoca fra ciascun oggetto e
un vocabolo numerico, dove il vocabolo numerico
corrispondente all’ultimo oggetto contato indica la
numerosità degli elementi
 Contare è la chiave della numerosità

20. Subitizing
L’automatismo del subitizing consiste in una
funzione visiva che consente un rapido e
preciso giudizio numerico eseguito su insiemi
di piccole numerosità di elementi.

21. Stima
La stima è un processo numerico a base
semantica che consiste nel determinare in
modo approssimativo e senza contare valori
incogniti (grandi numerosità).

22. Conteggio
Contare è fondamentale. Costituisce il primo
collegamento tra la capacità innata del
bambino di percepire le numerosità e le
acquisizioni matematiche più avanzate della
cultura nella quale è nato.
Imparare la sequenza delle parole usate per
contare è il primo modo con il quale i bambini
connettono il loro concetto innato di
numerosità con le prassi culturali della
società in cui sono nati.

23. Principi del conteggio
ASSOCIAZIONE UNO A UNO
 Associare parole-numero a oggetti
 Separare gli oggetti contati da quelli da contare
ORDINE STABILE
 Utilizzare in modo stabile una sequenza di numerali
CARDINALITA’
 Sapere che il numero di oggetti di un insieme corrisponde
all’ultimo numerale utilizzato per contare quell’insieme
IRRILEVANZA DELL’ORDINE
GENERALIZZAZIONE

24. Alla fine della classe prima, il mancato
raggiungimento delle seguenti abilità è indicativo di
difficoltà:
 Riconoscimento di piccole numerosità
 Lettura e scrittura di numeri entro il 10
 Calcolo a mente entro la decina (anche con
supporto di materiali)
(Consensus Conference, 2007)
Abilità numeriche e abilità di calcolo

25. Strategie
Se per la matematica è indifferente come sei
mele siano disposte sul tavolo per continuare
a essere sei, per la nostra mente è diverso.
Abbiamo bisogno di ordinare i nostri oggetti
mentali con un ordine prestabilito e stabile se
vogliamo conservarli in mente.
Il calcolo mentale è il superamento del
conteggio

26. Didattica e comprensione del numero
Comparazione
 Giudizio di numerosità
Seriazione
 Riordino di sequenze numeriche
Stima
 Approssimazione numerica

27. 41006
305
1009
Quattrocentosei
Trentacinque
Centonove
lorenzo caligaris - aid milano
Produzione del numero

28. Produzione scritta del
numero (codice sintattico)
I meccanismi sintattici
regolano il valore
posizionale delle cifre
Costituiscono la
grammatica interna del
numero che attiva il
corretto ordine di
grandezza di ogni cifra
Nella codifica verbale di
un numero ogni cifra
assume un “nome”
diverso a seconda della
posizione che occupa.
Nei sistemi di
comprensione e/o
produzione dei numeri, i
meccanismi lessicali
hanno il compito di
selezionare
adeguatamente i nomi
delle cifre per riconoscere
quello del numero intero.
Produzione verbale del
numero (codice lessicale)

29. cinquecentoquattro!
(5 x 100) + 4 =
504
Codice lessicale (produzione verbale)
Il numero ha valore nominale
Codice sintattico (produzione scritta)
Il numero ha valore posizionale
Produzione del numero

30. Dettato di numeri
Lettura di numeri
Trasformazione in cifre
 da parole-numero a numerali
 codifica sintattica del numero
Operazioni di transcodifica numerica
Didattica e produzione del numero

31. Regole semantiche
 Rappresentazione astratta del numero
 Giudizio di numerosità
Regole sintattiche
 Grammatica del numero
 Valore posizionale delle cifre
 Scrittura di numeri
Regole lessicali
 Riconoscimento del nome del numero
 Enumerazione e Conteggio
 Lettura dei numeri
Didattica e sistema dei numeri

32. Il sistema di calcolo
Automatismi
Tabelline, risultati memorizzati
(recupero)
Calcolo
Operazioni a mente Operazioni
scritte (procedure)
(strategie)

33. Automatismi, strategie, procedure
Calcolo
il risultato dell’operazione
richiesta è ottenuto
attraverso l’utilizzo di
strategie o procedure
Recupero
il risultato dell’operazione
richiesta è recuperato
direttamente dalla memoria
Fatti aritmetici
Calcolo a mente
Calcolo scritto

34. La verifica degli automatismi di calcolo deve
avvenire oralmente
La risposta deve essere rapida
(circa 5 secondi)
Se il tempo di risposta è maggiore, allora il risultato
è stato ottenuto attraverso l’utilizzo di una
procedura o di una strategia di calcolo.
Automatismi di calcolo

35. Ai fatti aritmetici si accede senza eseguire gli algoritmi di
soluzione:
 Tabelline
 Calcoli semplici (addizioni e sottrazioni entro la
decina)
 Risultati memorizzati
Automatismi di calcolo

36. L’uso di strategie costruttive del calcolo a mente consente di
operare scomposizioni sui numeri per ottenere operazioni
intermedie più semplici:
– proprietà delle operazioni
commutativa: 23 + 66 = 89 (66+23 = 89)
scomposizione del secondo operatore:
66 + 23= 89 (66+20 = 86), (86+3 = 89)
scomposizione di entrambi gli operatori:
66 + 23= 89 (60+20 = 80), (6+3 = 9), (80+9 = 89)
Strategie di calcolo

37. Possiamo quindi concludere che:
• La cognizione di quantità (semantica del numero)
consente l’accesso ai meccanismi di conteggio e al
sistema di transcodifica nei numeri in linguaggi
(lessico) e in segni regolati da una grammatica
interna (sintassi del numero)
• La conoscenza numerica è dominio specifica
• I bambini di 5 anni sanno già riconoscere diversi
aspetti implicati nel numero (i numeri si scrivono, si
dicono, servono per….)
• La didattica della matematica deve tener conto di
questi aspetti innati e cercare di potenziarli

38. Conoscenze di base sui numeri:
Conoscenze semantiche (rappresentazioni di
quantità, confronto fra grandezze, stime,…)
Conoscenze lessicali (conoscere i nomi dei
numeri e saperli leggere e scrivere)
Conoscenze sintattiche (conoscenza della
grammatica del numero, valore posizionale
delle cifre, numeri decimali, frazioni, potenze,
…)
Counting (enumerare avanti e indietro)

39. Abilità di base del calcolo:
Conoscenze procedurali del calcolo scritto
(procedure delle operazioni, meccanismi del
prestito e del riporto,…)
Strategie di calcolo a mente (n+1,
arrotondamenti alla decina, combinazioni di
numeri, raggruppamenti, scomposizioni, …)
Memorizzazione di fatti numerici (processo
automatizzato di recupero di semplici
combinazioni di numeri e tabelline)

40. Come procedi per eseguire le moltiplicazioni a mente?
Paolo: “Se i numeri sono piccoli e corti, uso le tabelline.
Se sono lunghi, le scrivo.”
Luca: “Faccio che se il numero è difficile, per esempio 24
x8, prendo il 4 e lo moltiplico, poi il 2 e lo
moltiplico.”
Marta: “Se è più difficile non ci riesco, e dunque scrivo.”

41. Analisi degli errori:
 errore : leggere 135 145
 Errore: 80 è maggiore di 90
 errore: scrivere 135 10035
 Errore: 4 @@@@@
 Errore: 7,2 è minore di 7,08

42. sistema del calcolo: analisi
degli errori
 errore : 23 x
12 =
26
 errore: 2 x 5 = 15
 errore : 2 x 5 = 7

43. DISCALCULIA
EVOLUTIVA:
SUGGERIMENTI PER
L’INTERVENTO DIDATTICO

44. Tra mille dubbi, due aspetti emergono con
certezza:
 L’indipendenza (pur non assoluta) delle abilità
numeriche dalle altre competenze e abilità;
 La relativa indipendenza di sistemi diversi
all’interno delle abilità numeriche
E’ dunque opportuno verificare quali moduli
o sistemi sono meglio funzionanti, e
utilizzarli per compensare i deficit negli altri
sistemi
Si parte quindi dall’analisi delle difficoltà

45. NB l’allenamento della memorizzazione di
fatti aritmetici è poco efficace
Più utile l’associazione dei fatti numerici a
rappresentazioni visive (linea dei numeri,
tavola pitagorica, tastiera calcolatrice,
oppure rappresentazioni analogiche)
Uso di strategie di recupero indiretto e
riduzione dei fatti aritmetici da memorizzare
Importante la concettualizzazione dei
numeri come entità scomponibili
Difficoltà di calcolo:

46. allenamento e potenziamento di strategie di
calcolo più evolute (o più semplici, se
queste sono meglio controllate)
allenamento delle associazioni visivo-
verbali riferite a concetti e trasformazioni di
tipo matematico
Osservazione di trasformazioni con
materiale concreto
utilizzazione di rappresentazioni grafiche
delle trasformazioni quantitative
Difficoltà di calcolo:

47. Permettere l’uso della calcolatrice (e del
computer)!!!!!
Privilegiare le componenti concettuali e
strategiche
Permettere tempi di esecuzione più lunghi
(privilegiando l’autonomia rispetto alla
velocità)
E soprattutto alla Scuola Secondaria di 1° e 2°
grado…

48. Abilità logico-matematiche
Componenti delle abilità matematiche
strettamente legate alle abilità cognitive e
strategiche
(relativamente) indipendenti da abilità
numeriche e di calcolo (ma attenzione
anche alle comorbilità!)
Non interessate dalla discalculia in senso
stretto
Tuttavia importanti come supporto alle
abilità numeriche e di calcolo (su cui in
teoria si fonderebbero processo a ritroso)

49. Abilità Logico-matematiche
Comprensione del significato delle operazioni
Comprensione e uso del linguaggio
matematico
Capacità di selezione delle informazioni
rilevanti (dati) in un problema matematico
Capacità di rappresentazione dei problemi
Capacità di soluzione dei problemi
Conoscenza
Procedurale
Comprensione
Concettuale

50. Come supportare le DIFFICOLTA’ DI
RAGIONAMENTO LOGICO-
MATEMATICO
APPROCCI METACOGNITIVI

51. Metacognizione
Conoscenza e consapevolezza…
 Della natura dei processi
 Del funzionamento della mente
 Delle proprie difficoltà
 Delle strategie possibili
 Delle modalità di attuazione
 Delle modalità di controllo (monitoraggio)
Dunque include processi di conoscenza e
processi di controllo

52. Riconoscere le abilità cognitive implicate in
situazioni matematiche e le loro interconnessioni
(da Lucangeli e Passolunghi, 1995)
1. Riconoscere il ruolo dell’attenzione nella
competenza matematica
2. Riconoscere il ruolo del linguaggio verbale nella
competenza matematica
3. Riconoscere il ruolo delle abilità visuospaziali
nella competenza matematica

53. Riconoscere le abilità cognitive implicate in
situazioni matematiche e le loro interconnessioni
(da Lucangeli e Passolunghi, 1995)
4. Riconoscere che la mente umana lavora in
maniera interconnessa: matematica e memoria
5. Riconoscere il ruolo della memoria di lavoro
(MBT) nelle abilità matematiche
6. Riconoscere il ruolo e la capacità della memoria
a breve e a lungo termine
7. Riconoscere l’importanza della percezione di
autoefficacia nella competenza matematica

54. Riconoscere abilità mentali
specifiche per il problem-solving
(da Lucangeli e Passolunghi, 1995)
1. Prendere consapevolezza della natura dei
problemi matematici
2. Riconoscere l’importanza di un procedimento
operativo per trovare la soluzione a un problema
3. Riconoscere l’importanza dei diversi piani di
rappresentazione

55. Riconoscere abilità mentali
specifiche per il problem-solving
(da Lucangeli e Passolunghi, 1995)
4. Riconoscere la consequenzialità dei
procedimenti matematici
5. Riconoscere che esistono più percorsi di
soluzione
6. Riconoscere che il problem solving dipende
dall’organizzazione delle conoscenze della
persona
7. Riconoscere l’importanza della precisione nelle
procedure