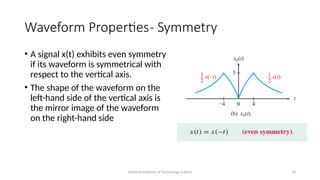
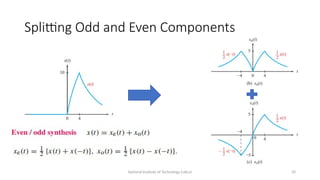
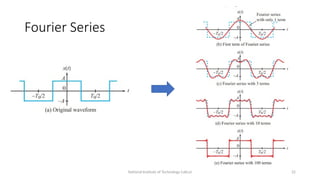
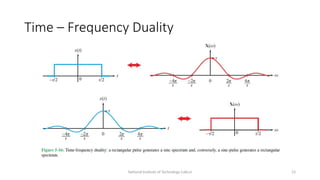
The document discusses the applications and principles of digital signal processing (DSP) across various fields, including audio processing, telecommunications, and biomedical engineering. It covers essential topics like signals and systems, discrete-time signal analysis, digital filters, and the importance of the Nyquist sampling theorem. Key concepts such as deterministic vs. random signals, frequency in discrete-time signals, and waveform properties are also highlighted.

1. National Institute of Technology Calicut
Digital Signal Processing
Dr. Rakesh R Warier

2. National Institute of Technology Calicut 2
Applications of Digital Signal Processing
• Audio and speech processing,
• Sonar, radar and other sensor array processing,
• Spectral density estimation,
• Digital image processing,
• Data compression,
• Signal processing for telecommunications,
• Control systems,
• Biomedical engineering,
• and Seismology, among others

3. National Institute of Technology Calicut 3
Contents
• Review of Signals and Systems
• Analysis and representation of discrete-time signal systems, including
discrete-time convolution,
• Difference equations, the z-transform, and the discrete-time Fourier
transform. Emphasis is placed on the similarities and distinctions
between discrete-time,
• Digital filters, (FIR and IIR),
• Fast Fourier transform algorithm.

4. National Institute of Technology Calicut 4
The most important algorithm!

5. National Institute of Technology Calicut 5
Review of signals and systems
• What is a signal?
• What is a system?
• Analog vs Digital

6. National Institute of Technology Calicut 6
Signals
• Continuous vs Discrete Signals
• A signal x(t) is analog and
continuous-time if both x and t
are continuous variables (infinite
resolution). Most real world
signals are analog and
continuous-time.
• Dependent vs independent
variable

7. National Institute of Technology Calicut 7
Examples Continued
12 lead ECG signal

8. National Institute of Technology Calicut 8
Discrete Signals
• Representations
• Bracket notation
• Stem plot

9. National Institute of Technology Calicut 9
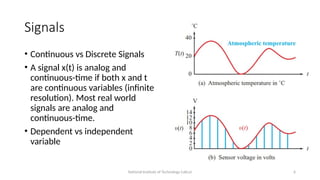
Digital vs Discrete-time
• A signal x[n] is analog and discrete-
time if the values of x are continuous
but time n is discrete (integer-valued).
• A signal x[n] is digital and discrete-time
if the values of x are discrete (i.e.,
quantized) and time n also is discrete
(integer-valued). Computers store and
process digital discrete-time signals.
Not covered in this course.

10. National Institute of Technology Calicut 10
Deterministic vs Random Signals
• Any signal that can be represented by
a unique model (formula, table or
mathematical expression) without any
uncertainty is called deterministic
signal.
• In many practical applications, there
are signals that cannot be described
by any reasonable accuracy by any
explicit mathematical formula, and
they evolve in an unpredictable
manner and are called random signals.

11. National Institute of Technology Calicut 11
Continuous time Sinusoids
• Continuous time sinusoids with
different frequencies are distinct.
• Increasing frequency results in
increasing oscillations

12. National Institute of Technology Calicut 12
Periodic Signals (continuous)
• A periodic signal of period satisfies
the periodicity property:
for all integer values of n and all times
t.

13. National Institute of Technology Calicut 13
Frequency (discrete time signal)
• A discrete signal is periodic with period N>0 if
, for all
Smallest value for which this is true is called the fundamental
period.

14. National Institute of Technology Calicut 14
Example
• Find the frequency (=50)
• Solve for N

15. National Institute of Technology Calicut 15
Example
• Find the frequency ()
• Solve for N

16. National Institute of Technology Calicut 16
Example
• Find the frequency ()
• Solve for N
• A discrete-time sinusoid is periodic only if the frequency is a rational
number!

17. National Institute of Technology Calicut 17
Frequency in discrete-time signals

18. National Institute of Technology Calicut 18
Waveform Properties- Symmetry
• A signal x(t) exhibits even symmetry
if its waveform is symmetrical with
respect to the vertical axis.
• The shape of the waveform on the
left-hand side of the vertical axis is
the mirror image of the waveform
on the right-hand side

19. National Institute of Technology Calicut 19
Waveform Properties – Odd Symmetry
• Odd Symmetry
• A signal exhibits odd symmetry if
the shape of its waveform on the
left-hand side of the vertical axis is
the inverted mirror image of the
waveform on the right-hand side.

20. National Institute of Technology Calicut 20
Splitting Odd and Even Components

21. National Institute of Technology Calicut 21
Fourier Formula

22. National Institute of Technology Calicut 22
Fourier Series

23. National Institute of Technology Calicut 23
Time – Frequency Duality

24. National Institute of Technology Calicut 24
Fourier Series

25. National Institute of Technology Calicut 25
Sampling
• Consider a sinusoidal signal
x(t) = cos(2π1000t),
sampled at fs = 8000 samples per
second.
• The sampling interval is Ts = 1/8000 s,

26. National Institute of Technology Calicut 26
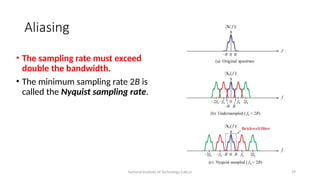
Sampling Theorem
• Let x(t) be a real-valued, continuous-time,
low pass signal bandlimited to a maximum
frequency of B Hz.
• Let x[n] = x(nTs) be the sequence of numbers
obtained by sampling x(t) at a sampling rate
of fs samples per second, that is, every Ts =
1/fs seconds.
• Then x(t) can be uniquely reconstructed from
its samples x[n] if and only if fs > 2B.
• The sampling rate must exceed double the
bandwidth.
• The minimum sampling rate 2B is called the
Nyquist sampling rate.

27. National Institute of Technology Calicut 27

28. National Institute of Technology Calicut 28

29. National Institute of Technology Calicut 29
Aliasing
• The sampling rate must exceed
double the bandwidth.
• The minimum sampling rate 2B is
called the Nyquist sampling rate.

30. National Institute of Technology Calicut 30
Practice Problem

31. National Institute of Technology Calicut 31
Solution

32. National Institute of Technology Calicut 32
Sampling at Nyquist rate

33. National Institute of Technology Calicut 33
Homework

34. National Institute of Technology Calicut 34
References
• Digital Signal Processing: Principles, Algorithms, and Applications,
John G. Proakis. Northeastern University. Dimitris G. Manolakis.
Boston College, 4th
ed.