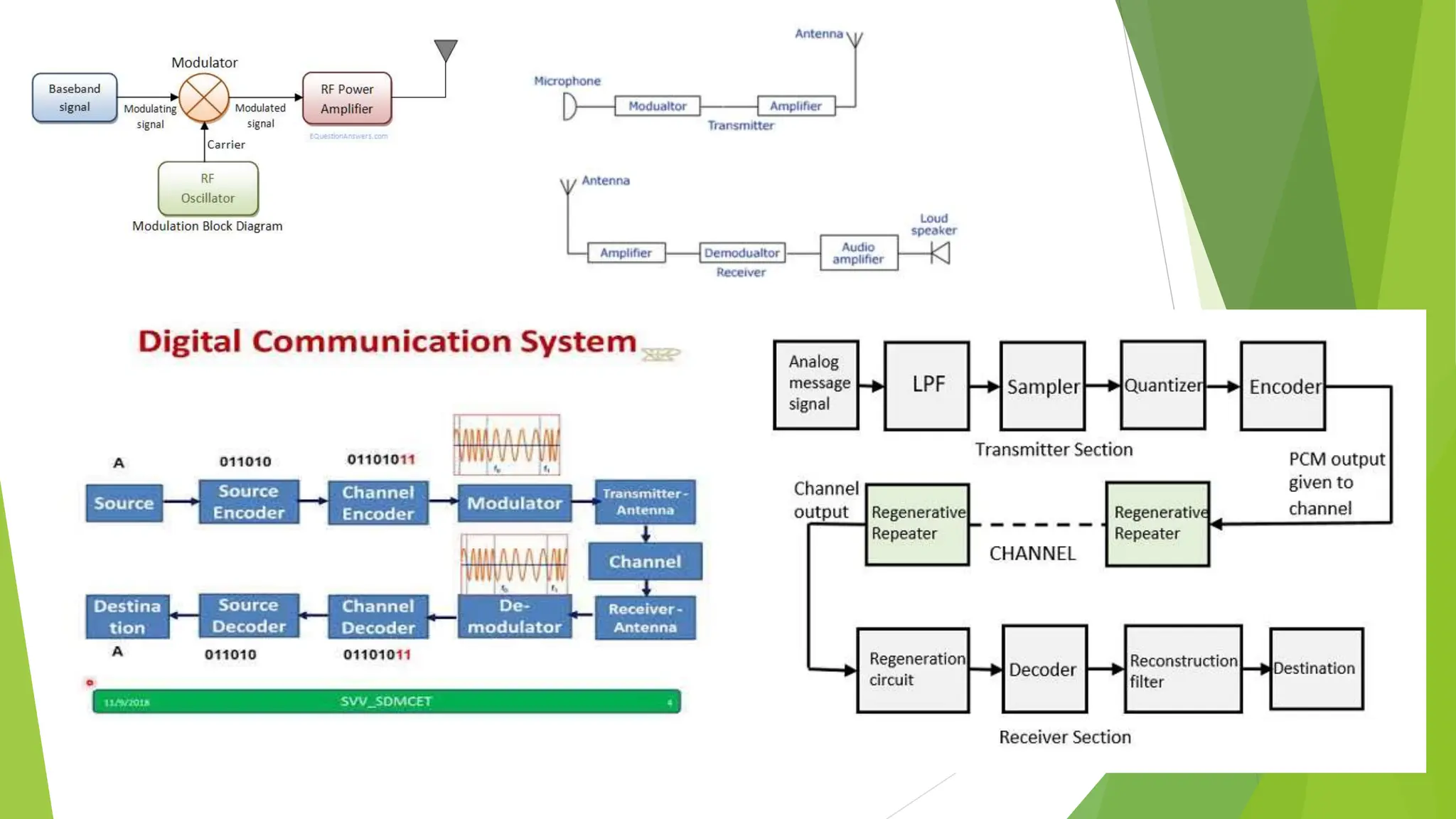
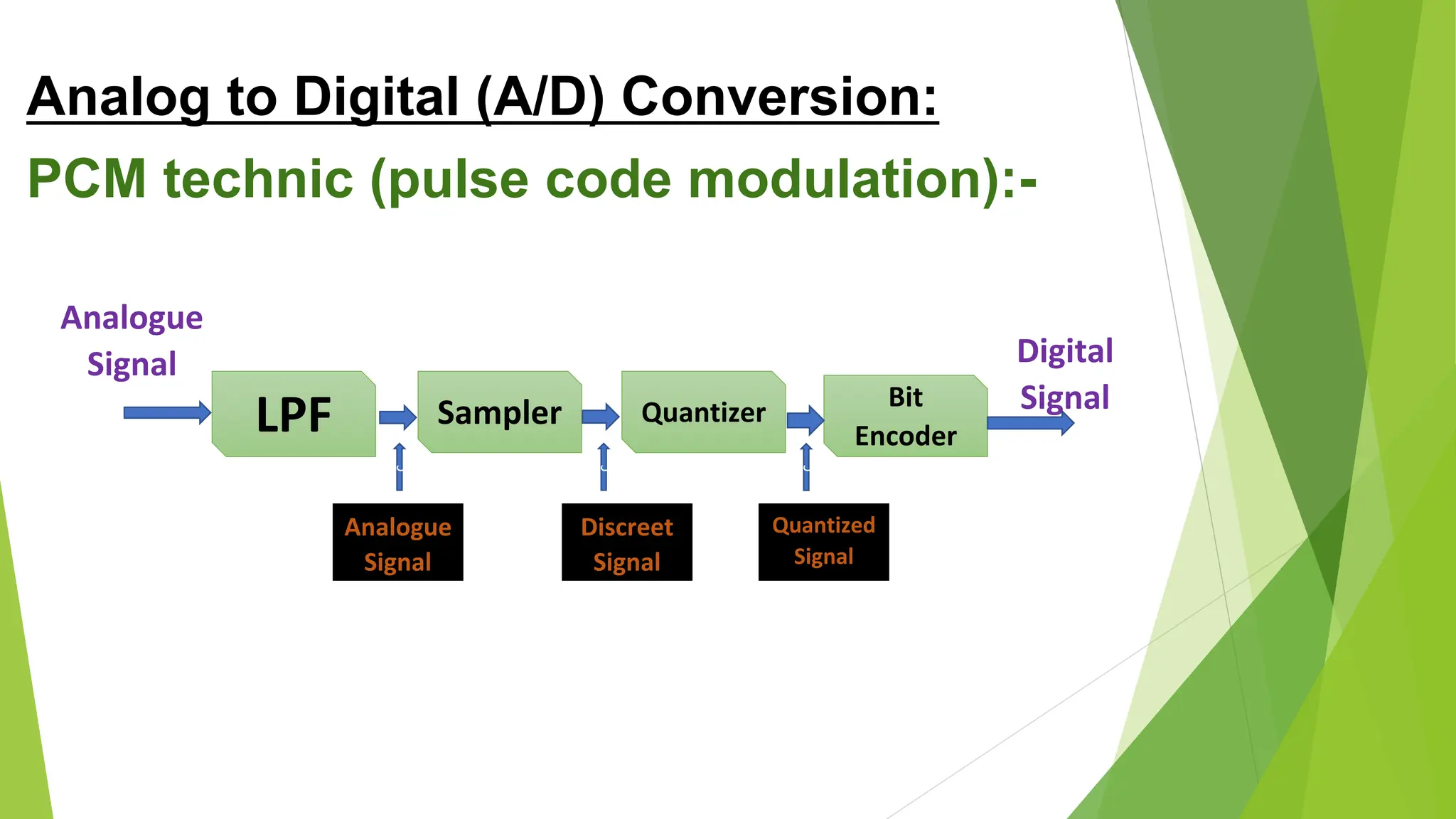
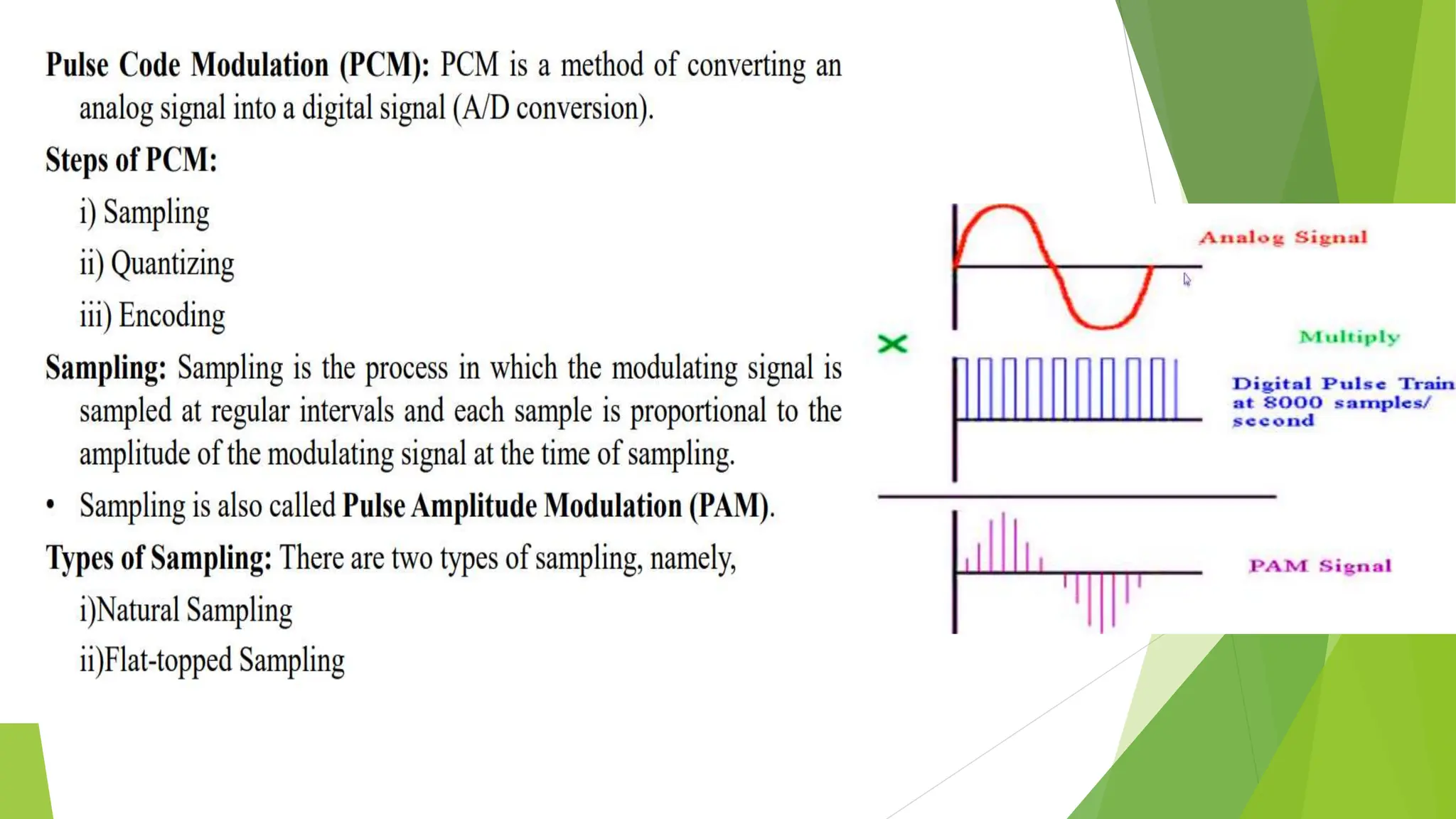
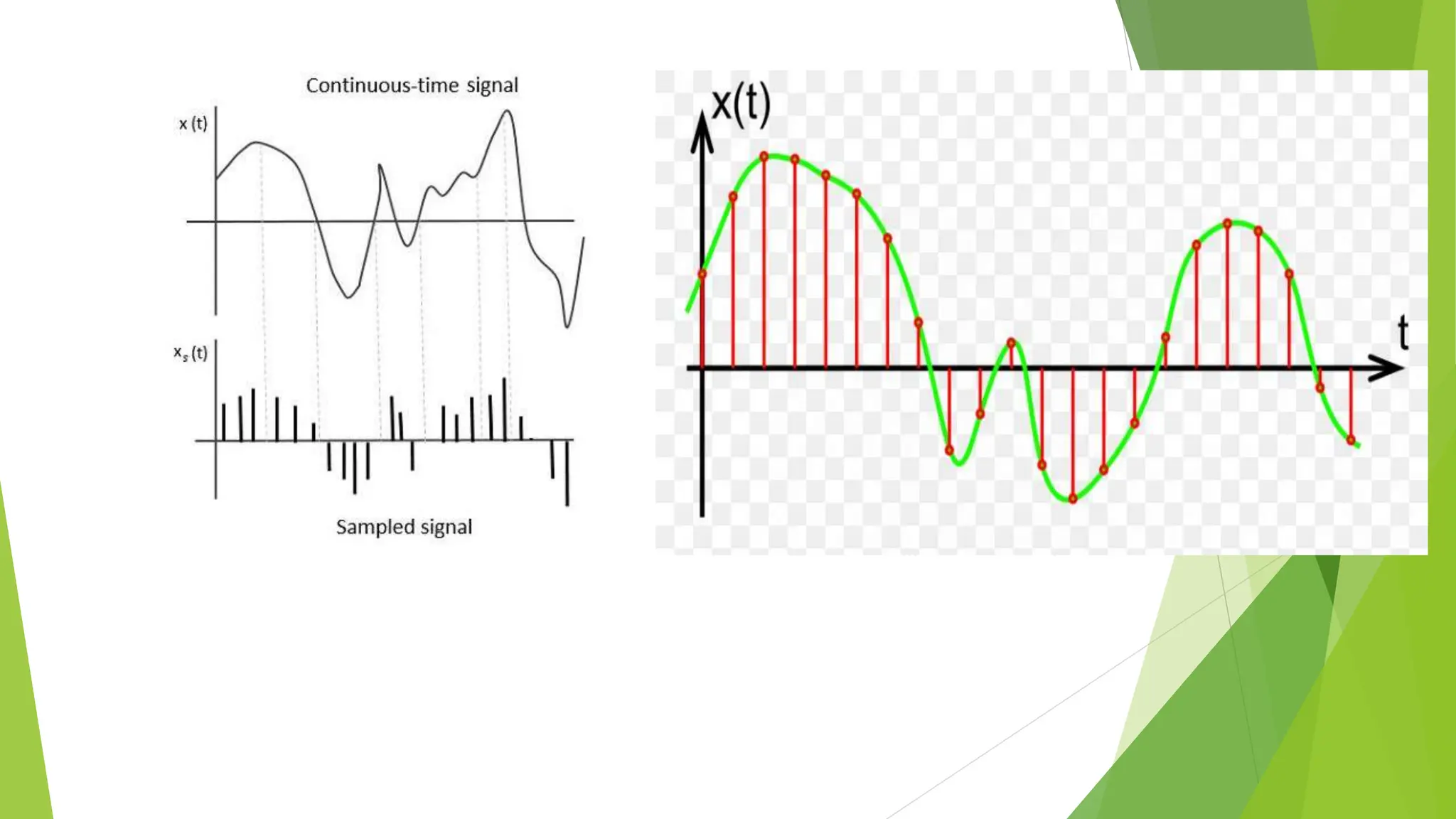
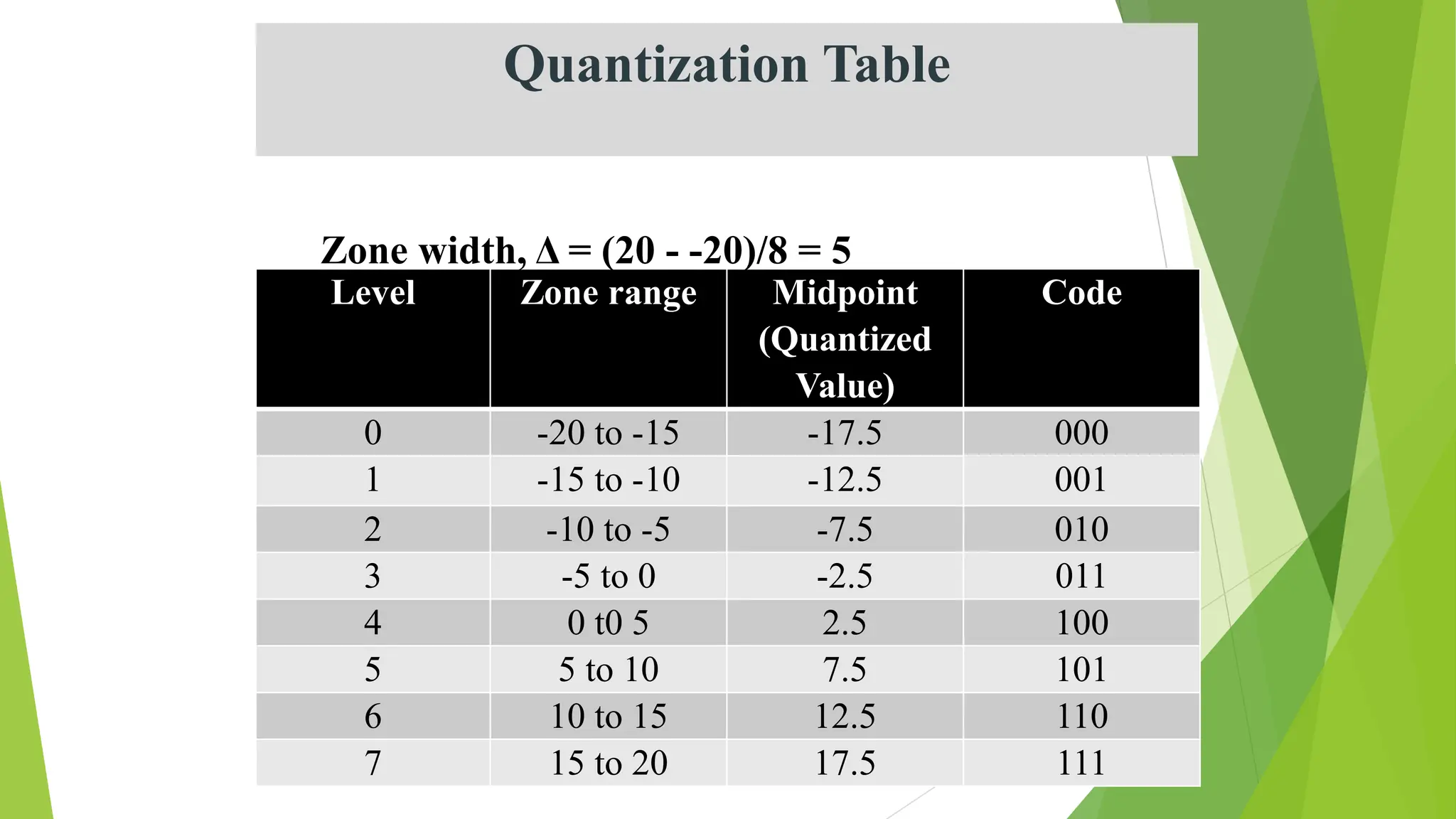
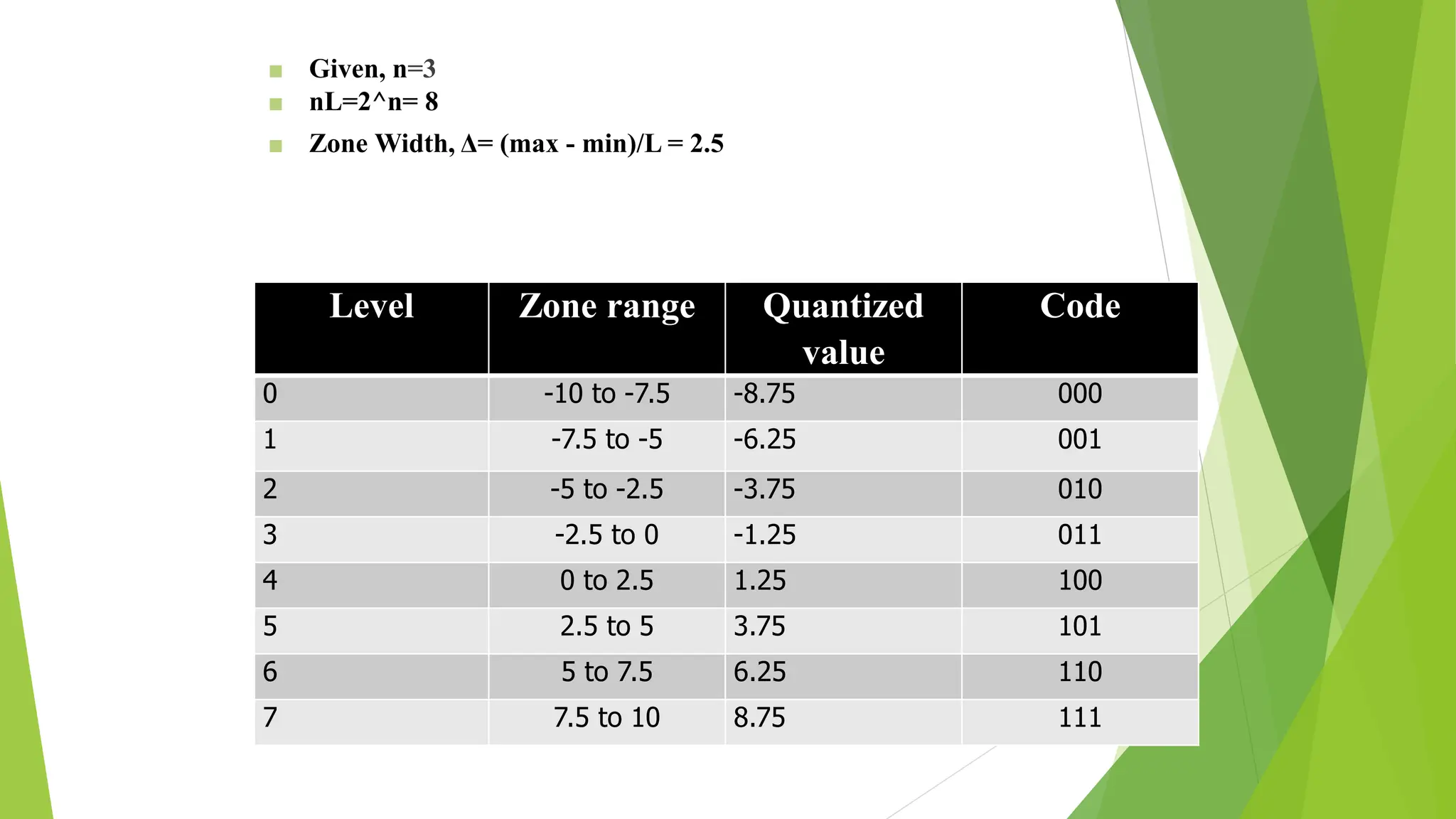
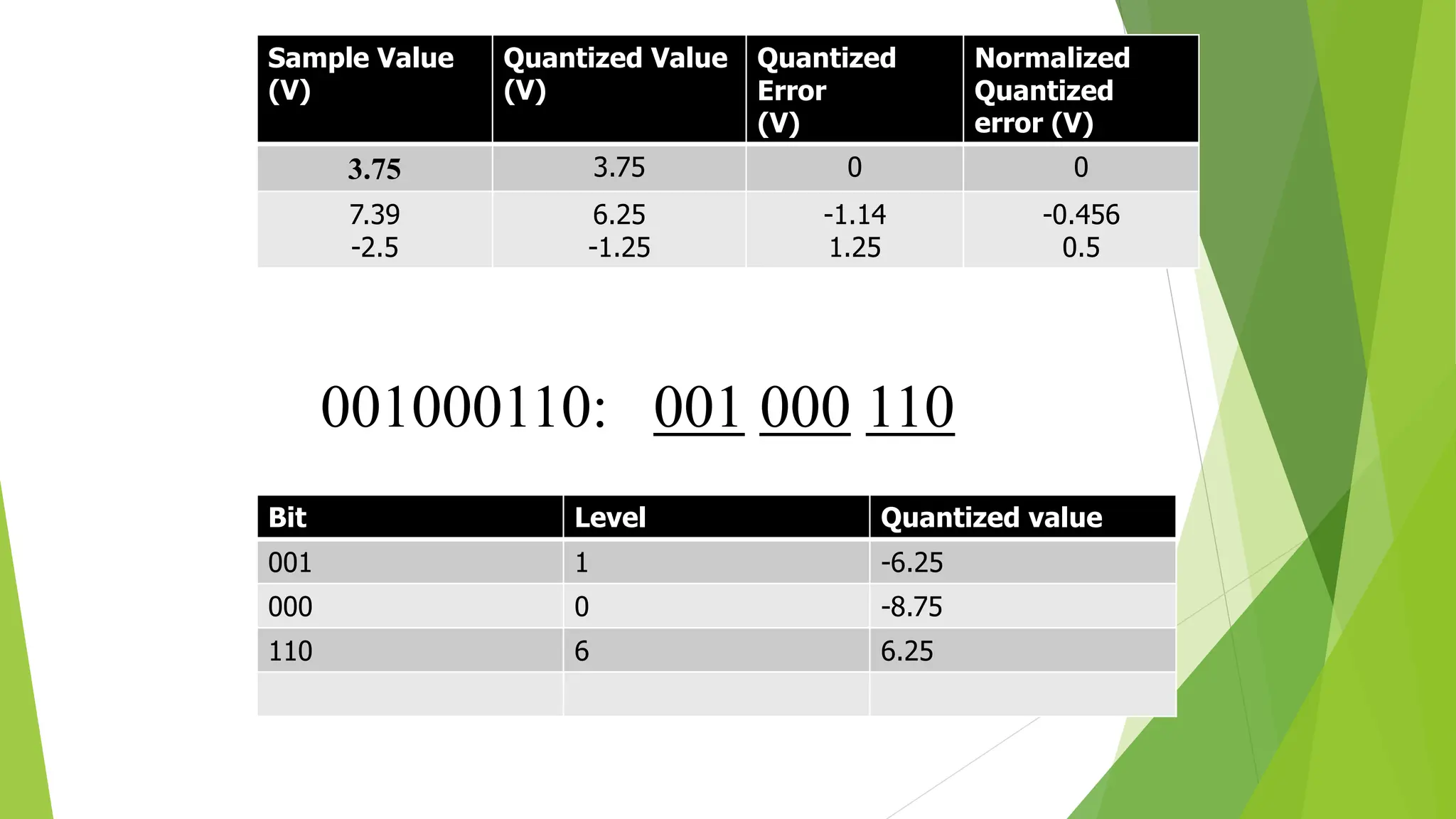
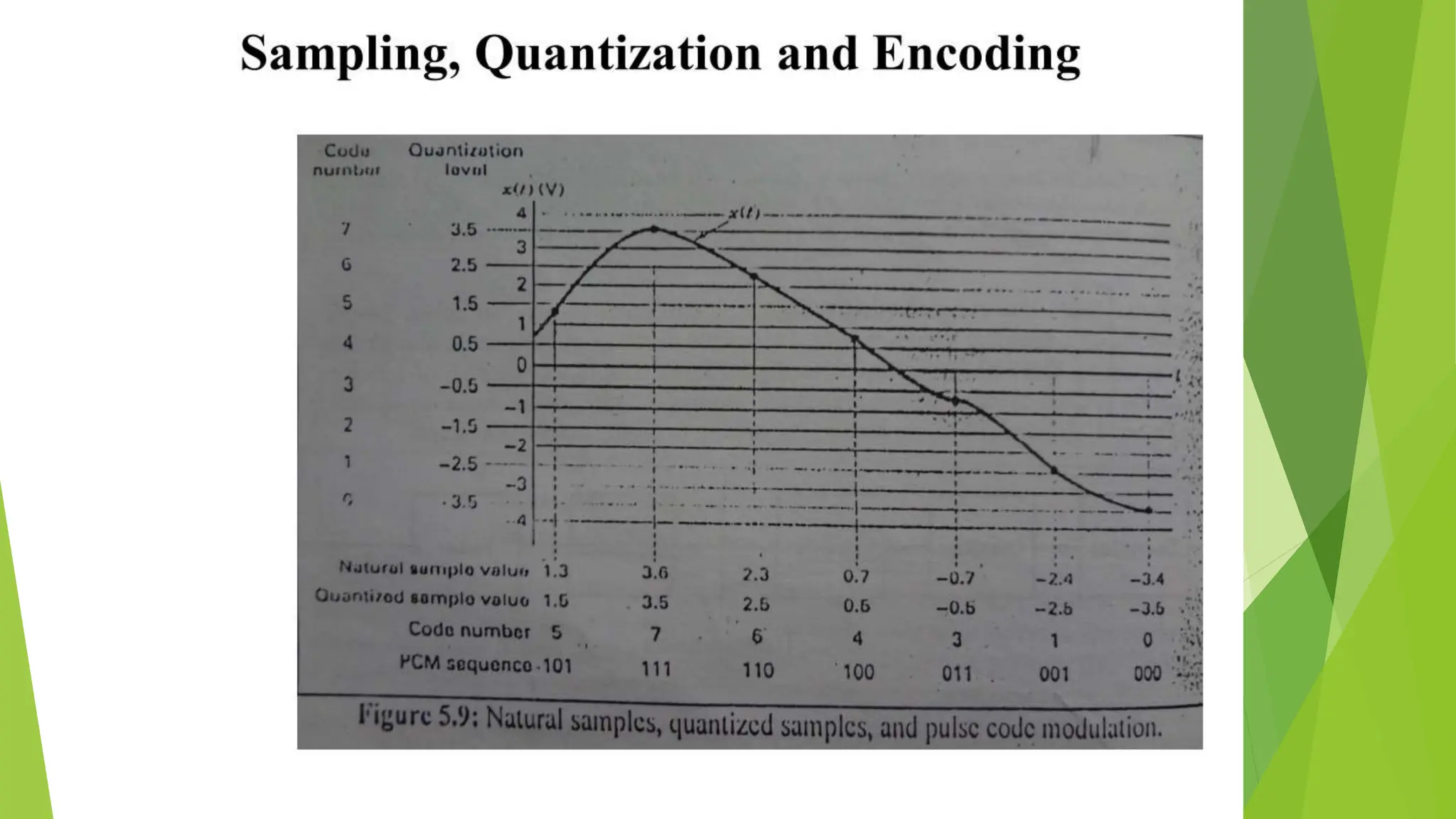
The document provides an overview of digital communication, comparing it with analog communication, and explaining the concepts of digital and analog signals, digital modulation techniques, and A/D conversion. It also discusses quantization, sampling, and the processes involved in converting and recovering signals, including examples and calculations pertaining to bit rates, sampling rates, and quantization errors. Finally, it addresses problems related to signal bandwidth and signal-to-noise ratio (SNR) for various scenarios.

1. Digital Communication
Digital Communication is that where the message or data is in digital form of
signal, then the digital message signal is modulated by using digital modulation techniques
Then transmitted by transmitter.
So
1.What is the basic Difference between Digital and Analog Communication System?
2.What is Analog Signal?
3.What is Digital Signal?
4.What is Digital Modulation ? And what are the techniques?
5.What are the Differences between Digital and Analog Modulation Techniques?
6.Actually message signals from input transducer (microphone ,camera or Keyboard are what types ?
Analog or Digital?
7.If Analog how can we convert this into digital in Digital communication?

2.  An analog signal signifies a continuous signal that keeps changes with a time period.
 A digital signal signifies a discrete signal that carries binary data and has discrete values.
 Analog signals are continuous sine waves. Digital signal is square waves.

3. Basic Difference between Digital and Analog Communication System
Analog communication uses analog signal whose amplitude varies continuously with time
from 0 to infinite. Digital communication uses digital signal whose amplitude is of two
levels either Low i.e., 0 or either High i.e., 1.
Advantages of Digital Communication
Digital circuits are more reliable.
Digital circuits are easy to design and cheaper than analog circuits.
The configuring process of digital signals is easier than analog signals.
Digital signals can be saved and retrieved more conveniently than analog signals.

4. A/D
Converter
Channel
Encoder Modulator
[Input signal]
Analog or continuous
signal
Digital Bit
Digital signal pulse
Digital Modulated
signal
Digital Message signal
and
Carrier signal
Digital Communication (Digital Transmitter)
A/D Converter: Analog To Digital Converter

6. LPF Sampler Quantizer
Bit
Encoder
Digital
Signal
Discreet
Signal
Analogue
Signal
Quantized
Signal
c
c
c
Analogue
Signal
Analog to Digital (A/D) Conversion:
PCM technic (pulse code modulation):-

12. According to the Nyquist theorem, the
sampling rate must be
at least 2 times the highest frequency
contained in the signal.
Note

13. Figure 4.24 Recovery of a sampled sine wave for different sampling rates

14. Telephone companies digitize voice by assuming a
maximum frequency of 4000 Hz. Calculate the sampling
rate.
Solution:
Sampling rate is 8000 samples per second.
Example 4.9

16. It is the process to convert infinite value signal into a finite
value.
A/D output= n bits per sample (quantization level, L=2^n)
Quantization

17. Quantization
■ Sampling results in a series of pulses of varying amplitude values ranging
between two limits: a min and a max.
■ The amplitude values are infinite between the two limits.
■ We need to map the infinite amplitude values onto a finite set of known values.
■ This is achieved by dividing the distance between min and max into L zones,
each of height Δ.
Δ = (max - min)/L

18. Quantization Levels
■ The midpoint of each zone is assigned a
value from 0 to L-1 (resulting in L values)
■ Each sample falling in a zone is then
approximated to the value of the midpoint.

19. Assigning Codes to Zones
■ Each zone is then assigned a binary code.
■ The number of bits required to encode the zones, or the number of bits per
sample as it is commonly referred to, is obtained as follows:
nb = log2 L
■ Given our example, nb = 3

20. Quantization Zones
■ Assume we have a voltage signal with
amplitudes Vmin=-20V and Vmax=+20V.
■ We want to use L=8 quantization levels.
■ Zone width or Step Size, Δ = (max - min)/L
■ Δ = (20 - -20)/8 = 5

21. Quantization Table
Level Zone range Midpoint
(Quantized
Value)
Code
0 -20 to -15 -17.5 000
1 -15 to -10 -12.5 001
2 -10 to -5 -7.5 010
3 -5 to 0 -2.5 011
4 0 t0 5 2.5 100
5 5 to 10 7.5 101
6 10 to 15 12.5 110
7 15 to 20 17.5 111
Zone width, Δ = (20 - -20)/8 = 5

22. Quantization Error
■ When a signal is quantized, we introduce an error - the coded signal is an
approximation of the actual amplitude value.
■ The difference between actual and coded value is referred to as the
quantization error.
■ The more zones, the smaller Δ which results in smaller errors.
■ BUT, the more zones the more bits required to encode the samples -> higher
bit rate
■ A non-uniform quantization method is introduced to reduce the quantization
error.

23. ■ Quantization Error = Quantized Value- Sample value.
■ Normalized Sample value= Actual sample value / Δ
■ Normalized Quantized value= Actual quantized value / Δ
■ Normalized Quantization Error = Normalized Quantized
Value- Normalized Sample value.
Or, Normalized Quantization Error = Quantization Error / Δ
Acceptable range for Quantization Error=
Quantization Error

24. Problem on Quantization
Q.1. Suppose we have a signal whose voltage level lies
between -10 and 10 Volt. We want to perform PCM
quantization and represent each signal sample by three bits.
i. Find the zone width for this quantization. Also calculate the
zone range and quantized value.
ii. Calculate the quantized values when the analog sample
voltage are 3.75V, 7.39V and -2.5V. Also calculate the
quantization error and normalized quantization error.
iii. Suppose after sampling and encoding the signal, you find a
bit stream of “001000110”. What were the quantized values?

25. ■ Given, n=3
■ nL=2^n= 8
■ Zone Width, Δ= (max - min)/L = 2.5
Level Zone range Quantized
value
Code
0 -10 to -7.5 -8.75 000
1 -7.5 to -5 -6.25 001
2 -5 to -2.5 -3.75 010
3 -2.5 to 0 -1.25 011
4 0 to 2.5 1.25 100
5 2.5 to 5 3.75 101
6 5 to 7.5 6.25 110
7 7.5 to 10 8.75 111

26. Sample Value
(V)
Quantized Value
(V)
Quantized
Error
(V)
Normalized
Quantized
error (V)
3.75 3.75 0 0
7.39
-2.5
6.25
-1.25
-1.14
1.25
-0.456
0.5
Bit Level Quantized value
001 1 -6.25
000 0 -8.75
110 6 6.25
001000110: 001 000 110

28. Bit rate and bandwidth requirements
of PCM
■ The bit rate of a PCM signal can be calculated from the
number of bits per sample x the sampling rate
Bit rate = nb x fs
■ The bandwidth required to transmit this signal depends on
the type of line encoding used.
■ Bandwidth of digital Signal =
Bits per sample X Bandwidth of Analog Signal
Bdigital = nb x Banalog
■ A digitized signal will always need more bandwidth than
the original analog signal. Price we pay for robustness and
other features of digital transmission.

30. A television signal has a bandwidth of 4.5MHz.This signal is
sampled quantized and binary coded to obtain PCM signal.
1.Determine sampling rate if the signal is sampled at a rate 20%
above the normal sampling rate.
2.Determine binary pulse rate in Kbps if the sample is quantized
into 1024 level.
We know..
v=2mp/L
Where,
L=Number of quantization level
v=Quantization interval
Here L=1124

31. Solution:-
Ans:
1) Sampling rate = {(4.5x106) x2} +2(4.5x106) x0.2
=10.8x106 sample/sec
2)Total bit = 10.8x106x10
=10.8x107 bps
=10.8x104 Kbps
=108x103 Kbps
=108 Mbps

32. SNR
SNR in dB can be calculated by using this formula:

33. PCM Decoder
■ To recover an analog signal from a digitized signal we follow the following
steps:
■ We use a hold circuit that holds the amplitude value of a pulse till the next pulse
arrives.
■ We pass this signal through a low pass filter with a cutoff frequency that is equal to
the highest frequency in the pre-sampled signal.
■ The higher the value of L, the less distorted a signal is recovered.

34. Figure 4.27 Components of a PCM decoder

35. We want to digitize the human voice. What is the bit rate,
assuming 8 bits per sample?
Solution
The human voice normally contains frequencies from 0
to 4000 Hz. So the sampling rate and bit rate are
calculated as follows:
Example 4.14

36. We have a low-pass analog signal of 4 kHz. If we send the
analog signal, we need a channel with a minimum
bandwidth of 4 kHz. If we digitize the signal and send 8
bits per sample, we need a channel with a minimum
bandwidth of 8 × 4 kHz = 32 kHz.
Bandwidth of digital Signal =
Bits per sample X Bandwidth of Analog Signal
Example 4.15

37. Q.1.A telephone subscriber line must
have an SNR in dB above 40. What is
the minimum number of bits per
sample? Also Calculate the bit rate of
digitized signal.
Practice Problem

38. SNR in dB= 40,
SNR (in dB)= 6.02 n + 1.76
So, n=6.35, This is not valid number.
So, n= 6 or 7
fm=3 kHz, fs=2 *fs= 6 kHz
Bit rate, N= n * fs
If n=6 then N=6 *6=36 kbps
If n=7, then N=7*6=42 kbps
Solution

39. Practice Problem
We have sampled a low-pass signal with
a bandwidth of 200 kHz using 1024
levels of quantization.
a. Calculate the bit rate of the digitized
signal.
b. Calculate the SNRdB for this signal.
c. Calculate the PCM bandwidth of this
signal.

40. L=1024, So, n=10
B=200kHz, fm= 200kHz
fs= 2*fm=400 kHz
a. Bit Rate, N=n*fs=10*400= 4000 kbps
= 4 Mbps
a. SNR(dB)= 6.02n+1.76=61.96 dB
b. B (digital)=n* B(analog)= 10*200
=2000 kHz= 2 MHz
Solution

41. Practice Problem
An analog signal has a
bandwidth of 20 kHz. If we
sample this signal and send it
through a 30 kbps channel what
is the SNRdB ?

42. B=20kHz, fm=20kHz, fs= 40 kHz
N= 30 kbps
N=n*fs
n=N/fs=30/40= 0.75=1
SNR (in dB)= 6.02 n + 1.76= 7.78 dB
Solution